ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Оптимизация сетевого графика по критериям
«время – стоимость» Для изучения материалов этого параграфа воспользуйтесь презентацией, представленной в файле «Сетевая модель-3». Оптимизация проводится с целью: ü сокращения длины критического пути, ü выравнивания коэффициентов напряженности работ, ü рационального использования ресурсов. В первую очередь принимаются меры по сокращению продолжительности работ, находящихся на критическом пути, это достигается: Ø перераспределением всех видов ресурсов, как временных (использование резервов времени некритических путей), так и трудовых, материальных, энергетических (например, перевод части исполнителей, оборудования с некритических путей на работы критического пути); Ø при этом перераспределение ресурсов должно идти, как правило, из зон, менее напряженных, в зоны, объединяющие наиболее напряженные работы; Ø сокращением трудоемкости критических работ за счет передачи части работ на другие пути, имеющие резервы времени; Ø параллельным выполнением работ критического пути; Ø пересмотром топологии сети, изменением состава работ и структуры сети. Оптимизация сетевого графика в зависимости от полноты решаемых задач может быть условно разделена на частную и комплексную. Видами частной оптимизации сетевого графика являются: Ø минимизация времени выполнения комплекса работ при заданной его стоимости; Ø минимизация стоимости комплекса работ при заданном времени выполнения проекта. Комплексная оптимизация представляет нахождение оптимального соотношения величин стоимости и сроков выполнения проекта в зависимости от конкретных целей, ставящихся при его реализации.
Слайд 51
Слайд 52
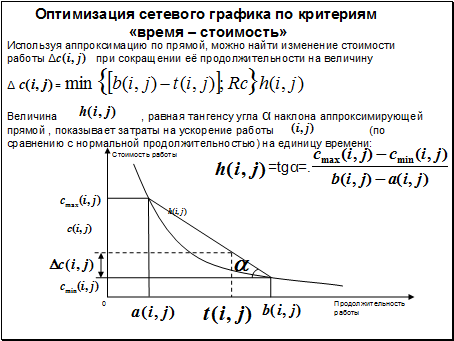
В реальных проектах каждая работа характеризуется не только временем, но и стоимостью выполнения. В этом случае полная стоимость проекта будет равна сумме стоимостей всех входящих в него работ. Могут быть поставлены и решены следующие две задачи оптимизации сетевого графика по критериям «время-стоимость»: 1. Минимизация стоимости проекта при сохранении времени его выполнения tkp. 2. Минимизация времени выполнения tkp при заданной стоимости проекта. При оптимизации сетевого графика предполагается: 1) уменьшение продолжительности работ ведет к увеличению их стоимости; 2) для каждой работы (i, j) ее продолжительность t(i, j) лежит в пределах a(i, j) ≤ t(i, j) ≤ b(i, j) , где а(i, j) – минимально возможная продолжительность работы; b(i, j)– максимально допустимая продолжительность выполнения работы; 3) стоимость С(i,j) работы заключена в пределах Cmax(i, j) и Cmin(i, j). При линейной зависимости стоимости работ от их продолжительности задача оптимизации сетевого графика может быть поставлена в виде задачи линейного программирования, в которой необходимо минимизировать стоимость проекта при двух группах ограничений. Первая группа ограничений- ограничения на время выполнения работ, вторая группа ограничений показывает, что продолжительность всех полных путей не должна превышать заданного времени выполнения проекта. Вопросы и задачи. Выберите какие формулы характеризуют: событие, работу или путь в сетевов графике?
Ответы:
|