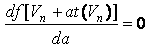ПОЗНАВАТЕЛЬНОЕ

Сила воли ведет к действию, а позитивные действия формируют позитивное отношение

Как определить диапазон голоса - ваш вокал

Игровые автоматы с быстрым выводом

Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими

Целительная привычка

Как самому избавиться от обидчивости

Противоречивые взгляды на качества, присущие мужчинам

Тренинг уверенности в себе

Вкуснейший "Салат из свеклы с чесноком"

Натюрморт и его изобразительные возможности

Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.

Как научиться брать на себя ответственность

Зачем нужны границы в отношениях с детьми?

Световозвращающие элементы на детской одежде

Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия

Как слышать голос Бога

Классификация ожирения по ИМТ (ВОЗ)

Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Способы градиентной оптимизации

Существует несколько модификаций метода градиентной оптимизации применительно к дискретным вычислениям.

Если подъем происходит поочередно по каждой отдельной координате v₁, v₂, … , v_k , то такой метод называют покоординатным подъемом или методом Гаусса – Зейделя. Движение осуществляется из некоторой точки по координате v₁ до тех пор, пока не станет равной нулю соответствующая производная ∆f(V)/ ∆v₁ = 0. Все остальные координаты (аргументы функции) сохраняют постоянное значение. После этого подъем начинается по другой координате. Порядок перебора координат не играет принципиальной роли, а влияет только на скорость поиска, поэтому обычно начинают с v₁, затем с v₂ и т.д. После того, как будет произведен подъем по всем координатам, начинают повторно с v₁. Процесс заканчивается, когда все частные производные будут равны нулю (будут меньше порога чувствительности).

Метод наискорейшего подъема предполагает определение градиента в исходной точке, далее подъем в этом направлении осуществляется до тех пор, пока производная df(V)/dV в этом направлении не обратится в нуль. После этого снова определяют градиент и осуществляют по нему подъем до нулевого значения производной и т.д. Модификация этого метода предусматривает вычисление градиента в каждой новой точке траектории перемещения.

Все сказанное о сущности методов поиска максимума функции легко транспонируется и для поиска минимума. Рассмотренные методы предполагают возможность движения по любому выбранному направлению, т. е. ограничений на область допустимых значений аргументов нет. В качестве начальной точки может быть взята любая точка пространства E_k. Равенство ∆f(V^*) = 0 является необходимым, но не достаточным условием экстремума функции в точке V^*, да и точек V^* может быть несколько. Поэтому требуются дополнительные исследования для установления, какая из точек действительно является оптимумом (а не точкой перегиба) и какая из них является глобальной.

Одна из основных проблем применения градиентного метода поиска заключается в выборе величины каждого дискретного шага. Шаги могут быть постоянными или переменными. Второй вариант в реализации алгоритма более сложный, но обычно требует меньшего количества итераций.

Поиск максимума функции включает следующие этапы.

1. Определение аналитических соотношений для вычисления градиента функции ∆f(V), длины вектора градиента |∆f(V)| и единичного вектора t(V).

2. Выбор исходной точки V_n при n = 0 (начальных значений аргументов функции).

3. Вычисление координат единичного вектора t(V_n) по формуле, полученной на шаге 1 и определение координат новой точки при движении по направлению единичного вектора.

4. Выбор шага a изменения координат текущей точки V_n. Осуществляется из условия предельного увеличения функции f[V_n + at(V_n)] одного аргумента a в соответствии с уравнением

Корень этого уравнения, максимизирующий функцию f(V), обозначим a_n. Следующее приближение V_n+1 вычисляется по формуле:

V_n+1 = V_n+а_n t(V_n).

Производится возврат к этапу 3.

В результате формируется последовательность приближений V₀, V₁, V₂, … . Вычислительный процесс заканчивается, когда будет достигнута точка V_n, в которой оценка градиента будет равна нулю (коэффициенты функции отклика становятся незначимыми).

Рассмотренный алгоритм применяют только для нелинейных функций. Если функция отклика является линейной, то выбор оптимального значения параметра a невозможен. В этом случае шаг выбирается исходя из эвристических предположений исследователя о виде функции отклика.