 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Понятие седловой точки. Теорема Куна-Таккера
Центральное место в теории нелинейного программирования занимает теорема Куна-Таккера. Пусть дана задача нелинейного программирования: найти максимальное значение функции Z=f(х1, х2, ..., хn) при ограничениях
Составим функцию Лагранжа для данной задачи:
Если выполняется условие регулярности (существует по крайней мере одна точкаX, для которой gi(X)>0 для всех i), то имеет место следующая теорема. Теорема.Вектор X(0) тогда и только тогда является оптимальным решением задачи (4.1), когда существует такой вектор Λ(0), что при
Точка (X(0),Λ(0)) называется седловой точкой для функции F(X,Λ), а теорема называется теоремой о седловой точке. Докажем достаточность условий (4.3). Доказательство. Пусть X(0)>0 и Λ(0)>0 - седловая точка функции F(X,Λ). Если в (4.3) вместо F(X,Λ) подставить ее значение (4.2), то получим
при Правое неравенство справедливо при любом
Тогда из левого неравенства получим
Так как при этом
то f(X(0))>f(X). Таким образом, точка X(0) удовлетворяет (4.1) и во всех других точках, удовлетворяющих (4.1), функция принимает значение меньшее, чем в X(0). Это утверждение приводит решение задачи НЛП к отысканию седловых точек функции Лагранжа F(X,Λ). Доказательство необходимости условий (4.3) ввиду его сложности не рассматривается. Если f(X) и gi(X)—дифференцируемые функции, то условия (4.3) эквивалентны следующим локальным условиям Куна-Таккера:
Выражение
означает, что значение частной производной функции Лагранжа берется в точке (X(0), Λ(0)), где X(0)=(х1(0), х2(0), ..., хn(0)), Λ(0)=(λ1(0), λ2(0), ..., λn(0)). Эти условия можно записать в векторной форме:
Пример. Найти maxZ=-x12-x22 при ограничениях
Покажем, что существует Λ(0)0, при котором в точке оптимума выполняются условия Куна-Таккера (4.4), (4.5) для функции F(X,Λ): F(X,Λ)=-x12-x22+λ1(2x1+x2-2)+λ2(8-2x1-x2)+λ3(6-x1-x2). Находим:
Согласно условиям (4.5) λ2 и λ3 должны принимать нулевые значения, так как, подставляя x1=0.8 и x2=0.4 в выражения
имеем значения, большие нуля, а по условию
Согласно условию λ1 может принимать ненулевое значение, так как
В соответствии с (2.16) производная
должна принимать нулевые значения, так как координаты вектора X(0) отличны от нуля. Находим λ1=0,8. Следовательно, в точке (X(0),Λ(0)) выполняются условия Куна-Таккера и она действительно является точкой экстремума. Рассмотрим условия Куна-Такера в несколько другом виде. Пусть имеем задачу оптимизации с ограничениями в виде равенств: z = f(x1, x2, …, xn) → min при условиях: g1(x1, x2, ... , xn) = 0, g2(x1, x2, ... , xn) = 0, . . . . . . gn(x1, x2, . . . , xn) = 0. Точка условного минимума функции f совпадает с седловой точкой функции Лагранжа:
При этом седловая точка должна обеспечивать минимум по своим переменным xi и максимум по переменным λj. Необходимые условия стационарной точки - равенство нулю частных производных первого порядка по всем переменным:
Отметим, что из второго уравнения следует, что только допустимые точки будут удовлетворять необходимым условиям. Для получения достаточного условия существования минимума необходимо добавить требование положительной определенности гессиана целевой функции. Рассмотрим общую задачу математического программирования: Z = f(X) → min, при условиях:
Ограничения в виде неравенств могут быть преобразованы в ограничения в виде равенств добавлением к каждому из них ослабляющих переменных
Сформируем функцию Лагранжа:
Тогда необходимые условия минимума принимают вид:
Второе уравнение можно преобразовать, отбросив ослабляющие переменные и переходя к ограничениям-неравенствам. Получим ограничения исходной задачи. Третье уравнение можно умножить на ui/2 и заменить ослабляющие переменные, выразив их из второго уравнения системы. Есть еще одно условие, которое должно выполняться в точке минимума. Это условие: λi = 0, которое является следствием анализа физического смысла коэффициентов функции Лагранжа. Можно показать, что
где:
f* - оптимальное значение функции.
Окончательно получаем необходимые условия для условного минимума:
Выражения во второй строке гарантируют, что оптимальная точка будет допустимой. Третья строка содержит следующую информацию: если ограничение активно (т.е. выражение в скобках равно нулю), то соответствующий коэффициент Лагранжа строго положителен. Положительность коэффициента Лагранжа означает активность соответствующего ограничения, т.е. то, что это ограничение является дефицитным, именно оно останавливает дальнейшее улучшение целевой функции. Если же ограничение не активно (т.е. выражение в скобках не равно нулю), то соответствующий коэффициент Лагранжа должен быть равен нулю, т.е. это ограничение не дефицитно, оно не оказывает влияния на дальнейшее улучшение целевой функции. Для точки условного максимума коэффициенты Лагранжа меняют знак на противоположный (т.к. оптимальное значение целевой функции в точке условного максимума должно возрастать). Приведенные условия эквивалентны теореме Куна-Такера и часто называются так же. Достаточным условием для минимума (максимума) является выпуклость (вогнутость) целевой функции в стационарной точке. Это значит, что гессиан должен быть положительно (отрицательно) определен. Конспективное представление материала этой главы можно посмотреть в двух презентациях: файл «Нелинейное программирование»; файл «Теорема Куна-Таккера». На слайдах 10-14 презентации «Теорема Куна-Таккера» показан пример решения задачи Куна-Таккера.
Слайд 10
Слайд 11
Слайд 12
Слайд 13
Слайд 14
4.5. Контрольные вопросы (Разработаны Афанасьевым М.Ю. и Суворовым Б.П. [2]) Вопрос 1. Дана действительная функция f(х), определенная на отрезке действительных чисел S = [0, 100]. Пусть х1 и х2 — точки этого отрезка и 0 £ l £ 1. Какое из нижеприведенных неравенств является условием выпуклости функции? Варианты ответов:
Вопрос 2. Дана действительная функция f(x), определенная на отрезке действительных чисел S=[0, 100]. Пусть x1 и x2 — точки этого отрезка и 0 £ l £ 1. Какое из нижеприведенных неравенств является условием строгой вогнутости функции? Варианты ответов:
Вопрос 3. Функция
1) выпуклая; 2) строго выпуклая; 3) вогнутая; 4) строго вогнутая; 5) выпуклая и вогнутая. Вопрос 4. Функция
1) выпуклая; 2) ни выпуклая, ни вогнутая; 3) вогнутая; 4) строго вогнутая; 5) выпуклая и вогнутая. Вопрос 5. Функция
всюду: 1) выпуклая; 2) ни выпуклая, ни вогнутая; 3) строго выпуклая; 4) вогнутая: 5) выпуклая и вогнутая. Вопрос 6. Новая модель скоростного мотоцикла «Улитка» продается предприятием по цене (30 – 2x) тыс. долл. за штуку, где х - количество проданных мотоциклов. Переменные производственные затраты составляют 6 тыс. долл. за штуку, фиксированные затраты — 30 тыс. долл. Максимизируйте прибыль предприятия за неделю. Предположим, что в результате изменения ставки налога с продаж последний (налог) составил дополнительно 4 тыс. долл. на каждый проданный мотоцикл. Как изменится оптимальный выпуск мотоциклов по сравнению с начальной ситуацией? (Решить, используя функцию Лагранжа.) Варианты ответов: 1) увеличитсяна 2; 2) уменьшится на 2; 3) не изменится; 4) увеличится на 1; 5) уменьшится на 1. Вопрос 7. Предположим, что у вас есть 2 недели (14 дней) отпуска, которые вы можете провести на Канарских островах и в Ницце. Пусть ваша функция полезности имеет вид 2KN – 3К2 – 4N2, где К и N — количество дней, которое вы проводите на Канарских островах и в Ницце соответственно. Сколько дней вы должны провести в Ницце, чтобы максимизировать свою функцию полезности? (Для решения использовать функцию Лагранжа. Результат округлить до ближайшего целого. Проверить, выполняются ли условия оптимальности Куна — Таккера.) Варианты ответов: 1) 3; 2) 4; 3) 5; 4) 6; 5) 7. Вопрос 8. Для задачи вопроса 7 найдите значение двойственной оценки ограничения. (Результат округлить до ближайшего целого.) Варианты ответов: 1) 41; 2) 34; 3) 29; 4) 39; 5) 44. Вопрос 9. Монополист планирует программу производства и реализации продукции на следующий период. Цены: р1 = 14 – 0,25x1 (на продукт 1); р2 = 14 – 0,5х2 (на продукт 2), где x1 и х2 — объемы реализации продуктов. Предположим, что вся произведенная продукция реализуется. Максимальный суммарный объем сбыта — 57. Каков оптимальный выпуск продукта 2? Варианты ответов: 1) 36,4; 2) 30,7; 3) 26,3; 4) 20,6; 5) 41,8. Вопрос 10. Владелец небольшого предприятия располагает на ближайший месяц 100 тыс. руб., которые он может потратить на увеличение основных фондов К (закупку оборудования) по цене 1 тыс. руб за единицу либо на покупку дополнительной рабочей силы L по цене 50 руб./ч. Увеличение готовой продукции, которая может быть продана по 10 тыс. руб. за единицу, определяется производственной функцией F(K, L)= L2/7 К2/5. Сколько средств следует потратить на увеличение основных фондов? Варианты ответов: 1) 74,36 тыс. руб.; 2) 58,33тыс. руб.; 3) 63,44 тыс. руб.; 4) 45,66 тыс. руб.; 5) 39,77 тыс. руб. Ответы на вопросы: 1—4,2 — 1,3—4,4 — 5, 5—2, 6—5,7—4,8—2,9—4,10—2. |



 (4.1)
(4.1) (4.2)
(4.2) для всех
для всех 
 (4.3)
(4.3)
 .
. , поэтому
, поэтому





 (4.4)
(4.4) (4.5)
(4.5)




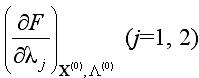








 - коэффициент Лагранжа в точке минимума;
- коэффициент Лагранжа в точке минимума; Очевидно, что при возрастании bi допустимая область расширяется, а это значит, что минимальное значение может только уменьшаться, то есть производная должна быть отрицательной (неположительной). Следовательно, в точке условного минимума
Очевидно, что при возрастании bi допустимая область расширяется, а это значит, что минимальное значение может только уменьшаться, то есть производная должна быть отрицательной (неположительной). Следовательно, в точке условного минимума









