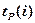ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Основные параметры сетевых графиков
В СПУ применяются связные, ориентированные графы без циклов, имеющие одну начальную и одну конечную вершину. Основные понятия сетевой модели: событие, работа, путь. Работа характеризует любое действие, требующее затрат времени или ресурсов. Работами считаются и процессы, не требующие затрат времени и ресурсов, а устанавливающие зависимости выполнения работ. Такие работы называются фиктивными. Работа обозначается парой чисел (i, j), где i – номер события, являющимся начальным для данной работы, j – номер события, являющимся конечным для данной работы, в которое она входит. Работа не может начаться раньше, чем свершится событие, являющееся для нее начальным. Каждая работа имеет свою продолжительность t(i, j). Работы на графах обозначаются дугами (стрелками), фиктивные работы обозначаются пунктирными стрелками. Событиями называются начало или завершение одной или нескольких работ. Они не имеют протяженности во времени. Событие совершается в тот момент, когда оканчивается последняя работа, входящая в него. На графе события изображаются кружками, внутри которых записывается номер события. В моделях СПУ имеется одно начальное событие (номер 0), одно конечное событие или завершающее (номер N) и промежуточные события (номер i). В графической интерпретации сетевой модели работы представляются дугами, а события – вершинами графа. Путь – цепочка следующих друг за другом работ (дуг), соединяющих начальную и конечную его вершины. Полный путь L – путь, начало которого совпадает с начальным событием сети, а конец – с завершающим. Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь, имеющий максимальную продолжительность, называют критическим (обозначение Lкр). Продолжительность критического пути обозначается как tкр.. Работы, принадлежащие критическому пути, называются критическими. Их несвоевременное выполнение ведет к срыву сроков всего комплекса работ. Сетевая модель должна удовлетворяет следующим требованиям: 1. Не должно быть событий с одинаковыми номерами. 2. Для каждой работы (i, j) должно выполняться условие i < j. 3. Должны быть только одно начальное и одно конечное события. 4. Должны отсутствовать циклы, т.е. замкнутые пути, соединяющие событие с ним же самим. При выполнении этих требований можно приступать к вычислениям числовых характеристик сетевых моделей (СМ). Исходные числовые данные СМ представляются в виде таблицы длительности выполнения каждой работы. При расчетах для сетевой модели определяются следующие характеристики ее элементов (табл. 7.1). Характеристики событий 1. Ранний срок свершения события tp(0) = 0, tp(j) = maxi{tp(i) + t(ij)}, j = 1 – N характеризует самый ранний срок завершения всех путей, в него входящих. Этот показатель определяется «прямым ходом» по графу модели, начиная с начального события сети. 2. Поздний срок свершения события tп(N) = tp(N), tп(i) = minj{tп(j) – t(ij)}, i = 1 – (N – 1) характеризует самый поздний срок, после которого остается ровно столько времени, сколько требуется для завершения всех путей, следующих за этим событием. Этот показатель определяется «обратным ходом» по графу модели, начиная с завершающего события сети.
Таблица 7.1.
3. Резерв времени события R(i) = tп(i) – tp(i) показывает, на какой максимальный срок можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения всего комплекса работ. Резервы времени для событий на критическом пути равны нулю, R(i) = 0. Графические формы отображения характеристик событий представлены на рисунках.
Характеристики работы (i, j) 1. Ранний срок начала работы: tpн(i, j) = tp(i). 2. Ранний срок окончания работы: tpo(i, j) = tpн(i, j) + tij = tp(i) + tij. 3. Поздний срок начала работы: tпн(i, j) = tп(j) – tij. 4. Поздний срок окончания работы: tпо(i, j) = tп(j). 5. Резервы времени работ: • полный резерв: Rп(i, j) = tп(j) – tp(i) – tij Максимальный запас времени, на который можно отсрочить начало или увеличить длительность работы без увеличения длительности критического пути. Работы на критическом пути не имеют полного резерва времени, для них Rп(i, j) = 0; • частный резерв: R1(i, j) = Rп(i, j) – R(i) = tп(j) – tп(i) – tij Часть полного резерва, на которую можно увеличить продолжительность работы, не изменив позднего срока ее начального события; • свободный резерв: Rс(i, j) = Rп(i, j) – R(j) = tp(j) – tp(i) – tij Максимальный запас времени, на который можно задержать начало работы или (если она началась в ранний срок) увеличит ее продолжительность, не изменяя ранних сроков начала последующих работ; • независимый резерв: Rн(i, j) = Rп(i, j) – R(i) – R(j) = tp(j) – tп(i) – tij Запас времени, при котором все предшествующие работы заканчиваются в поздние сроки, а все последующие – начинаются в ранние сроки. Использование этого резерва не влияет на величину резервов времени других работ. Работы, лежащие на критическом пути, резервов времени не имеют. Если на критическом пути Lкр лежит начальное событие i работы (i, j), то Rп(i, j) = R1(i, j). Если на Lкр лежит конечное событие j работы (i, j), то Rп(i, j) = Rc(i, j). Если на Lкр лежат и событие i, и событие j работы (i, j), а сама работа не принадлежит критическому пути, то Rп(i, j) = Rс(i, j) = Rн(i, j). Характеристики путей 1. Продолжительность пути равна сумме продолжительностей составляющих ее работ. 2. Резерв времени пути равен разности между длинами критического пути и рассматриваемого пути. Резерв времени пути показывает, на сколько может увеличиться продолжительность работ, составляющих данный путь, без изменения продолжительности срока выполнения всех работ. В сетевой модели можно выделить так называемый критический путь. Критический путь Lкр состоит из работ (i, j), у которых полный резерв времени равен нулю Rп(i, j) = 0, кроме этого, резерв времени R(i) всех событий i на критическом равен 0. Длина критического пути определяет величину наиболее длинного пути от начального до конечного события сети и равна tкр = tp(N) = tп(N). Заметим, что в проекте может быть несколько критических путей. 3. Коэффициент напряженности работ Для оценки трудности своевременного выполнения работ служит коэффициент напряженности работ: Кн(i, j) = (t(Lmax) – tкр) / (tкр – t'кр) = 1 – Rп(i, j) / (tкр – t'кр), где t(Lmax(i, j)) – продолжительность максимального пути Lmax(i, j), проходящего через работу (i, j); t'кр – продолжительность отрезка пути Lmax(i, j), совпадающего с критическим путем. Видно, что Кн(i, j) < 1. Чем ближе Кн(i, j) к 1, тем сложнее выполнить данную работу в установленный срок. Напряженность критических работ полагается равной 1. Все работы сетевой модели могут быть разделены на 3 группы: напряженные (Кн(i, j) > 0,8), надкритические (0,6 < Кн(i, j) < 0,8) и резервные (Кн(i, j) < 0,6). В результате перераспределения ресурсов стараются максимально уменьшить общую продолжительность работ, что возможно при переводе всех работ в первую группу. |