 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Принцип оптимальности Беллмана
Метод динамического программирования состоит в том, что оптимальное управление строится постепенно. На каждом шаге оптимизируется управление только этого шага. Вместе с тем на каждом шаге управление выбирается с учётом последствий, так как управление, оптимизирующее целевую функцию только для данного шага, может привести к неоптимальному эффекту всего процесса. Управление на каждом шаге должно быть оптимальным с точки зрения процесса в целом. Это основное правило динамического программирования, сформулированное Беллманом, называется принципом оптимальности. Итак, каково бы не было начальное состояние системы перед очередным шагом, управления на этом этапе выбирается так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был оптимальным. Так, если система в начале k - шага находится в состоянии Выбрав оптимальное управление Назовем величину
получившего название основного функционального уравнения динамического программирования, или основного рекуррентного уравнения Беллмана. Из уравнения (5.4) может быть получена функция
Решая уравнение (5.4) для определения условного максимума показателя эффективности за В результате последовательного решения п частных задач на условный максимум определяют две последовательности функций: Если начальное состояние
а затем - искомое безусловное оптимальное управление по цепочке
Если задано множество
откуда находят В рассмотренных рекуррентных соотношениях предписывают начинать вычисления с последнего этапа и затем передвигаться назад до этапа 1. Такой метод вычислений известен как алгоритм обратной прогонки. Если расчеты осуществляются в естественном порядке следования этапов, то такой метод вычислений известен как алгоритмпрямой прогонки. Приведем рекуррентные соотношения для этого случая. Уравнения состояний для прямого хода удобно записывать в виде
Введем в рассмотрение условные максимумы показателя эффективности за k шагов, от 1-го до k-говключительно, - величину
В результате решения этих уравнений получим последовательности
Далее определим безусловное оптимальное управление по цепочке
Существует два алгоритма решения задач: Алгоритм обратной прогонки: расчеты рекуррентных соотношений осуществляются с последнего этапа до первого. Алгоритм прямой прогонки: расчеты осуществляются в естественном порядке следования этапов. 1.Условная оптимизация. Определяются функция Беллмана и управления для всех возможных состояний на каждом шаге, начиная с последнего в соответствии с алгоритмом обратной прогонки. 1.1.На последнем, n-м шаге оптимальное управление определяется функцией Беллмана:
1.2.Дальнейшие вычисления производятся согласно рекуррентному соотношению, связывающему функцию Беллмана на каждом шаге с этой же функцией, но вычисленной на предыдущем шаге:
2. Безусловная оптимизация. Пользуясь тем, что на первом шаге (k = 1) состояние системы известно - это ее начальное состояние После применения этого управления система перейдет в другое состояние, зная которое, можно, пользуясь результатами условной оптимизации, найти оптимальное управление на втором шагеu2*, и так далее до последнего n-го шага. |



 и мы выбираем произвольное управление
и мы выбираем произвольное управление  , то она придет в новое состояние
, то она придет в новое состояние  , и последующие управления
, и последующие управления  должны выбираться оптимальными относительно состояния
должны выбираться оптимальными относительно состояния 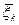 . Последнее, означает, что этими управлениями максимизируется величина
. Последнее, означает, что этими управлениями максимизируется величина  , то есть показатель эффективности на последующих до конца процесса шагах
, то есть показатель эффективности на последующих до конца процесса шагах  . Обозначим через
. Обозначим через  .
. на оставшихся
на оставшихся 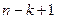 шагах, получим величину
шагах, получим величину  , которая зависит только от
, которая зависит только от  .
. условным максимумом.Еслимы теперь выберем на k-м шаге некоторое произвольное управление
условным максимумом.Еслимы теперь выберем на k-м шаге некоторое произвольное управление  , то система придет в состояние
, то система придет в состояние  так, чтобы оно в совокупности с оптимальным управлением на последующих шагах (начиная с (k+1)-го) приводило бы к общему показателю эффективности на
так, чтобы оно в совокупности с оптимальным управлением на последующих шагах (начиная с (k+1)-го) приводило бы к общему показателю эффективности на  ,
, , (5.4)
, (5.4) , если известно функция
, если известно функция  . Аналогично можно получить
. Аналогично можно получить  , если известно
, если известно 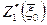 , представляющая по определению максимальное значение показателя эффективности процесса в целом:
, представляющая по определению максимальное значение показателя эффективности процесса в целом: .
. и называть условным оптимальным управлением на k-м шаге. Основное значение уравнения (5.4), в котором реализована идея динамического программирования, заключается в том, что решение исходной задачи определения максимума функции
и называть условным оптимальным управлением на k-м шаге. Основное значение уравнения (5.4), в котором реализована идея динамического программирования, заключается в том, что решение исходной задачи определения максимума функции  n переменных
n переменных  сводится к решению последовательности n задач, задаваемых соотношениями (5.4), каждое из которых является задачей максимизации функции одной переменной
сводится к решению последовательности n задач, задаваемых соотношениями (5.4), каждое из которых является задачей максимизации функции одной переменной  .
. - условные максимумы и соответствующие им
- условные максимумы и соответствующие им  - условные оптимальные управления. Указанные последовательности функций в дискретных задачах получают в табличной форме, а в непрерывных моделях - аналитически. После выполнения первого этапа (условной оптимизациии) приступают ко второму этапу - безусловной оптимизации.
- условные оптимальные управления. Указанные последовательности функций в дискретных задачах получают в табличной форме, а в непрерывных моделях - аналитически. После выполнения первого этапа (условной оптимизациии) приступают ко второму этапу - безусловной оптимизации. задано
задано  , то непосредственно определяют максимум целевой функции
, то непосредственно определяют максимум целевой функции ,
, . (5.5)
. (5.5) начальных состояний
начальных состояний 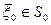 , то дополнительно решают еще одну задачу на максимум
, то дополнительно решают еще одну задачу на максимум ,
, .
.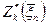 . Повторив приведенные рассуждения, придем к следующей системе уравнений Беллмана:
. Повторив приведенные рассуждения, придем к следующей системе уравнений Беллмана: ;
; .
. ;
;  .
. .
.

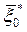 , можно найти оптимальный результат за все n шагов и оптимальное управление на первом шаге u1*, которое этот результат доставляет.
, можно найти оптимальный результат за все n шагов и оптимальное управление на первом шаге u1*, которое этот результат доставляет.