ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Метод ветвей и границ для задачи
календарного планирования Универсальность концепции метода ветвей и границ при решении практических задач предполагает необходимость разработки уникального способа ветвления дерева решений и вычисления соответствующих оценок нижней границы, которые зависят от специфики конкретной задачи. Рассмотрим применение метода ветвей и границ для решения задачи трех станков. Заданы п деталей di (i = 1, 2, ..., n), последовательно обрабатываемых на трех станках R1, R2, R3, причем технологические маршруты всех деталей одинаковы. Обозначим ai, bi, ci — длительность обработки деталей di на первом, втором и третьем станках соответственно. Определить такую очередность запуска деталей в обработку, при которой минимизируется суммарное время завершения всех работ Tц. Можно показать, что в задаче трех станков очередность выполнения первых, вторых и третьих операций в оптимальном решении может быть одинаковой (для четырех станков это свойство уже не выполняется). Поэтому достаточно определить очередность запуска только на одном станке (например, третьем). Обозначим sk = (i1, i2 , ..., ik) — некоторую последовательность очередности запуска длиной k (1 £ k £ п) и A (sk), В (sk), С (sk) — время окончания обработки последовательности деталей sk на первом, втором и третьем станках соответственно. Необходимо найти такую последовательность sопт, что С(sопт) = min С (s). Покажем, как можно рекуррентно вычислять A(sk), В(sk), С(sk). Пусть sk+1 = (sk ,ik+i), т. е. последовательность деталей sk+1получена из деталей sk с добавлением еще одной детали ik+1. Тогда: A (sk+1) = A (sk)+ В (sk+1) = max [A (sk+1); В (sk)]+ С (sk+1) = max [В (sk+1); С (sk)] + Для задачи трех станков можно использовать следующее правило доминирования: Если s— некоторая начальная последовательность, а А (s) £ А ( Причем хотя бы одно из них выполняется как строгое неравенство. Способ конструирования вариантов последовательностей s и вычисления оценок D(s) для каждого из них состоит в следующем: пусть имеется начальная подпоследовательность s. Тогда вычисляются величины: dC(s) = С(s) + dB(s) = В (s) + dA(s) = A (s) + где J (s) — множество символов, образующих последовательность s. За оценку критерия С (s) для варианта s можно принять величину D(s) = max {dA(s), dB (s), dC (s)}.(3.4) Тогда ход решения задачи трех станков можно представить следующей формальной схемой. Нулевой шаг. Задание множества G(0), образуется всеми возможными последовательностями (s = 0). Вычисление оценки для множества G0: Где D(0) = max {dA(0), dB (0), бC (0)},
Первый шаг. Образование множеств G1(1) U,G1(2)U... …G1(n). Подмножество Gk определяется всеми последовательностями с началом ik(k - 1, ...,n ). Вычисление оценок. Оценку для последовательности sk определяют из соотношения (3.4), т. е. D(sk) = max {dA(sk), dB (sk), dC (sk)}; k = 1, n. Выбор варианта для продолжения. Из всех подпоследовательностей, построенных на предыдущем шаге, выбирают наиболее перспективную последовательность sk с наименьшей оценкой, т. е. D(sk(1))=min D(sj(1)). Ветвление. Выбрав наиболее перспективный вариант последовательности sk(1), развивают его построением всех возможных подпоследовательностей длиной 2с началом sk(1) вида sk+1(2)= (sk(1), j), где j не входит в sk. Вычисление оценок производят в соответствии с соотношениями (3.1), (3.2), (3.3). k - шаг. Допустим, что уже проведено k шагов, в результате чего построены варианты s1(k), s2(k) ,…,svk(k), а именно подпоследовательности длиной k. Выбираем самый перспективный вариант sS(k) такой, что D(ss(k))=min D(sj(k)). Множество Gs(k) разбиваем на (п - k) подмножеств, каждое из которых образуется добавлением к последовательности ss(k) некоторого элемента ik+1 такого, что ik+1 Оценка В результате строим дерево вариантов следующего вида: вершина О отвечает s = 0, вершины первого уровня G1(1), G2(1)..., Gn(1) соответствуют последовательностям длиной 1, т. е. s1(1) = 1, s2(1) = 2,..., sn(1) = п и т. д. Каждая конечная вершина отвечает последовательности максимальной длины п. Признак оптимальности.Если sv(n) отвечает конечной вершине дерева, причем оценка Пример. Рассмотрим задачу трех станков, условия которой приведены в табл. 3.1: Таблица 3.1
Нулевой шаг. s = 0. dA(s = 0) = A(0) + dB(s = 0) = В(0) + dC(s = 0) = С(0) + Тогда: ∆ (s = 0) = max {17, 17,14} = 17. Первый шаг. Конструируем все возможные последовательности длиной 1 s1(1) = 1; s2(1) = 2; s3(1) = 3; s4(1) = 4; s5(1) = 5. Находим dA(1) = A1 + dB(1)(s = 0) = В1 + dC(1) = С1 + Откуда ∆ (1) = max {17, 19, 19} = 19. Аналогично определяем ∆ (2), ∆ (3), ∆ (4), ∆ (5). Второй шаг. Среди множества подпоследовательностей длиной 1 (s1(1) = 1, s2(1) = 2,..., s5(1) = 5) выбираем наиболее перспективную s = 1, для которой величина оценки-прогноза ∆ (s) оказывается наименьшей. Далее развиваем ее, конструируя возможные варианты длиной 2, т. е. (1.2), (1.3), (1.4), (1.5). Для каждого из этих вариантов вновь определяем оценки по формулам (3.1) — (3.4). Процесс вычислений продолжаем аналогично. Каждой конечной вершине дерева вариантов будет отвечать полная последовательность s = i1,i2,,.in. Если для некоторой такой вершины величина оценки ∆ (s) не превосходит величины оценок для всех остальных вершин, то эта оценка определяет искомый оптимальный вариант. В противном случае разбиваем более перспективный вариант с наилучшей оценкой. Конечная вершина определяет вариант (последовательность) Непосредственной проверкой убеждаемся, что время обработки всей последовательности деталей для этого варианта совпадает со значением оценки-прогноза и является минимальным:
3.6. Тест по теме «Метод ветвей и границ» |



 ,
, ,
,
 - подпоследовательность, образованная из s перестановкой некоторых символов, то вариант s доминирует над
- подпоследовательность, образованная из s перестановкой некоторых символов, то вариант s доминирует над  , (3.1)
, (3.1) + min cj , (3.2)
+ min cj , (3.2) +
+  (3.3)
(3.3) ;
;  ;
;  .
. .
. определяется в соответствии с соотношениями (3.1) - (3.4).
определяется в соответствии с соотношениями (3.1) - (3.4). наименьшая из оценок всех вершин, то sv(n) — искомый вариант, иначе переходим к продолжению варианта с наименьшей оценкой.
наименьшая из оценок всех вершин, то sv(n) — искомый вариант, иначе переходим к продолжению варианта с наименьшей оценкой. +
+  = 0 + 14 + 3 = 17;
= 0 + 14 + 3 = 17; + min cj = 0 + 15 + 2 = 17;
+ min cj = 0 + 15 + 2 = 17; =14 .
=14 . +
+  = 14 + 3 = 17;
= 14 + 3 = 17; +
+ 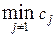 = 5 + 12 + 2 = 19;
= 5 + 12 + 2 = 19; = 9 + 10 = 19 .
= 9 + 10 = 19 .
 = 3, 1, 5, 2, 4 с наилучшей оценкой ∆ = 20. Поэтому данный вариант является оптимальным.
= 3, 1, 5, 2, 4 с наилучшей оценкой ∆ = 20. Поэтому данный вариант является оптимальным.