 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Общая постановка задачи исследования операций.
Исследование операций (ИО) (англ. Operations Research (OR)) — научный подход, основанный на разработке и применении методов нахождения оптимальных решений по результатам математического моделирования различных организационных систем. В процессе выбора решения R выделяются два потока исходных данных (Рис.1.1): А - постоянные (на которые нельзя оказать влияние); Х - переменные (например, потребности). При этом в выбранном решении рассогласование ∆А должно быть равно нулю, а моделирование вариантов допустимых решений осуществляется за счет варьирования величиной ∆Х. В связи с эти все факторы, учитываемые при моделировании систем методами исследования операций, делят на две группы: · постоянные факторы a1, a2,..., на которые нельзя оказать влияние; · зависимые факторы x1 ,x2,.., которые в известных пределах можно выбирать по своему усмотрению.
Рис. 1.1. Потоки информации, обеспечивающие процесс выбора решения. Критерий эффективности, выражаемый некоторой функцией, называемой целевой, зависит от факторов обеих групп, поэтому целевую функцию Z можно записать в виде: Z = f(x1 ,x2,.., a1, a2,...). Оптимизационную задачу можно сформулировать в общем виде: найти такие значения переменных x1 ,x2,.., xn, удовлетворяющие системе неравенств (уравнений) fi(x1 ,x2,.., xn)≤ bi ,i=1,2,...,m , которые обращают в максимум (или минимум) целевую функцию Z = f(x1 , x2,..,a1, a2,...)® max(min) Как правило, на переменные накладывается условие неотрицательности. Как известно, упорядоченная совокупность значений n переменных x1 ,x2,.., xn представляется точкой n - мерного пространства. В дальнейшем эту точку будем обозначать X = (x1 ,x2,.., xn), а само оптимальное решение X* = (x1*,x2*,.., xn*). К качестве примера рассмотрим характерную для исследования операций задачу – классическую задачу потребления, имеющую важное значение в экономическом анализе. Пусть имеется n видов товаров и услуг, количества которых (в натуральных единицах) x1 ,x2,.., xn по ценам соответственно p1 , p2,.., pn за единицу. Суммарная стоимость этих товаров и услуг составляет Уровень потребления Z может быть выражен некоторой функцией Z = f(x1 , x2,..,a1, a2,...), называемой функцией полезности. Необходимо найти такой набор товаров и услуг x1 ,x2,.., xn при данной величине доходов I, чтобы обеспечить максимальный уровень потребления, т.е. Z = f(x1 , x2,..,a1, a2,...)® max при условии
xi Решения этой задачи, зависящие от цен p1 ,p2,.., pn и величины дохода I, называются функцией спроса. Очевидно, что рассмотренная задача, так же как и многие другие, является частным случаем сформулированной выше общей задачи на определение экстремума функции n переменных при некоторых ограничениях, т.е. задачей на условный экстремум. В тех случаях, когда функции f,fi хотя бы дважды дифференцируемы, можно применять классические методы оптимизации. Однако применение этих методов в исследовании операций весьма ограничено, так как задача определения условного экстремума функции n переменных технически весьма трудна: метод дает возможность определить локальный экстремум, а из-за многомерности функции определение ее максимального (или минимального) значения (глобального экстремума) может оказаться весьма трудоемким – тем более, что этот экстремум возможен на границе области решений. Классические методы вовсе не работают, если множество допустимых значений аргумента дискретно или функция Z задана таблично. В этих случаях для решения задачи применяются методы математического программирования. Обычно выделяют три этапа экономико-математического моделирования. На первом этапе ставятся цели и задачи исследования, проводится качественное описание объекта в виде экономической модели. На втором этапе строится математическая модель объекта, осуществляется выбор существующих или разработка новых методов поиска оптимального решения. На третьем этапе проводятся расчеты, и осуществляется анализ полученных результатов. При построении модели операция, как правило, упрощается, а схема операции описывается с помощью того или иного математического аппарата. Модель операции – это достаточно точное описание операции с помощью математического аппарата (различного рода функций, уравнений, систем уравнений и неравенств и т.п.). Составление модели операции требует понимания сущности описываемого явления и знания математического аппарата. Эффективность операции – степень ее приспособленности к выполнению задачи – количественно выражается в виде критерия эффективности – целевой функции. Например, в задаче об использовании ресурсов критерий эффективности – прибыль от реализации произведенной продукции, которую нужно максимизировать, в транспортной задаче – суммарные затраты на перевозку грузов от поставщиков к потребителям, которые нужно минимизировать. Выбор критерия эффективности определяет практическую ценность исследования. Неправильно выбранный критерий может принести вред, ибо операции, организованные под углом зрения такого критерия эффективности, приводят порой к неоправданным затратам. В настоящее время в литературе насчитывается несколько десятков определений понятия “модель”, отличающиеся друг от друга. Под моделью в дальнейшем будем понимать условный образ какого-либо объекта, приближенно воссоздающий этот объект с помощью некоторого языка. В экономико-математических моделях таким объектом является экономический процесс (например, использование ресурсов, распределение деталей между различными типами оборудования и т.п.), а языком - классические и специально разработанные математические методы. Экономико-математическая модель – математическое описание исследуемого экономического процесса или объекта. Эта модель выражает закономерности экономического процесса в абстрактном виде с помощью математических соотношений. Использование математического моделирования в экономике позволяет углубить количественный экономический анализ, расширить область экономической информации, интенсифицировать экономические расчеты, принимать более обоснованные экономические решения. Процедура экономико-математического моделирования заменяет дорогостоящие и трудоемкие реальные эксперименты расчетами. Приведенные определения позволяют сформулировать основную задачу исследования операций – найти в рамках принятой модели такие решения, которым отвечают экстремальные значения критерияК. |




 .
.
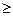 0 (i = 1,2,...n)
0 (i = 1,2,...n)