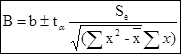ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Источник: учебник Вильямсона стр. 305
Следует отметить, кроме приведенных видов уравнений, которые предусматривает воздействие на результатирующий показатель только одного переменного, существуют и метод предусматривающее одновременного воздействия на целевую (зависимую функцию) множества факторов. Общий вид данного уравнения выглядит по следующему: у = а0 + а1 х1 + а2 х2 + а3 х3 + …+ аn хn ; Это связано в первую очередь Уравнение регрессии должна объяснить нам, почему у нас есть эта проблема:
Где ‘e’ это остаточный член …
111.Тесты на достоверность. Нам необходима оценить насколько достоверны полученные результаты в результате вычислении. Учитывая то обстоятельство, мы на основании фактических данных вычисляем теоретическую линию зависимостей для определения затрат при прогнозировании, анализе, обоснования управленческих решении и т.д. Здесь можно воспользоваться следующими тестами на достоверность. Таковыми тестами служат: ü Коэффициент смешанной корреляции; ü Среднеквадратические ошибки оценки; ü Среднеквадратические ошибки коэффициента. 1. Коэффициент смешанной корреляции. 1.1.Теретическая линия, если полностью совпадает с фактическим наблюдениями, она должна находится на теоретической линии, при их графическом отображении. 1.2. При несовпадении линии наблюдения с теоретически вычисленной линией, определяется размер этих отклонении при помощи квадратов разницы. 1.3.Среднее значение этих отклонении между фактическими и линией регрессии в статистике обозначается σи определяется;
Где, Υ- фактическое значение ; Υ1 – теоретическое значение ; Значение теоретического отклонения можно вычислить по следующей формуле: Σ (Y - Y')2 σ 2=------------------; где N- число наблюдении. N 1.4.Дисперсия (отклонение) фактических наблюдении от среднего значения, определяемый за исключением отклонения переменных вычисляется по следующей формуле: Σ (Y - ˉΥ)2 σ 2=------------------; где N- число наблюдении; ˉΥ – среднее значение фактического зависимого N показателя 1,5. Коэффициент смешанной корреляции: Σ (Y - Y')2 / N r 2 = 1 - --------------------- ; Σ (Y - ˉΥ)2 / N Коэффициент корреляции. степень связи или теснота связи между рассматриваемыми признаками (r) определяется : r = √¯ r 2¯ 2.Среднеквадратические ошибки оценки. Необходимость определения: - теоретическая линия определенная методом наименьших квадратов получена на основании конкретной выборки поэтому возможны отклонения от истинных линии. - Среднеквадратическая ошибка позволяет определить диапазон значений зависимой переменной (у), в рамках которой есть определенная степень достоверности, т.к. она является мерой отклонения относительно линии регрессии. - для определения t – распределения ( t –cстатистики), корректировочного значения падающего на недостающее значение тесноты связи. Абсолютное величина возможного отклонения от линии регрессии определяется с помощью показателя среднеквадратической ошибки ожидаемого значения, Se, с помощью следующей формулы: ___________ /Σ (Y - Y')2 Se= / ------------------; √ N -2 Величинаt – распределения ( t –cстатистики) определяется по таблице максимальных значении соответствующее доверительным интервалам с указанными вероятностями. Степень свободы: Количество наблюдении минус количество переменных в простой регрессии.
3. Среднеквадратические ошибки коэффициента. Для определения достоверности ожидаемого значения коэффициента регрессии переменных издержек, вычисляется среднеквадратическая ошибка коэффициента b, Sb, по следующей формуле:
Se Sb= -_--_--_--_--_--_-- ; где, Sb- среднеквадратическая ошибка коэффициента b; √ [Σ (х -ˉх)2 ] Упростив данную формулу получаем: Se Sb= -_--_--_--_--_--_ √ [Σ х2 -ˉх Σ х ) ] Например: Для решения можем воспользоваться формулами которые предложены в методических рекомендациях «КАРАНА» (1) и в книге Друри (ст,915) (2):a) Стандартная ошибка Теперь для примера воспользуемся данными задачи 24,8
Стандартная ошибка коэффициента 'b'
При подсчете доверительного интервала используйте:
|





 (2)
(2) (1)
(1) (2)
(2)