 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Электрлі магнитті рельстік тежегіштер
160 км/сағ жылдамдығы жететін поездар вагондарында электрлімагнитті рельстік тежегіштер орнатылады. Вагон арбашасына өзара байланыстырылған екі электрлімагнитті башмактар орнатылады. Башмактар цилиндрлер ішінде орналасқан серппелердің көмегімен жоғарғы жағдайда тұрады. Поездардың тежеу жүйесін қоректендіру кезінде магистральдан сығылған ауа дроссельді тесік арқылы және қайтымды клапан арқылы резервуарды толтырады. Жедел тежеу кезінде жеделдеткіш әрекеттке өтеді түйіспелер тұйықталады, көмегімен вентилдер қозатын блокты қосады және резервуа мен цилиндрді қосатын пневматикалық реле. Ауаның қысымынан цилиндр поршендері башмактарды рельстерге түсіреді, және осы мерзімде башмактардың катушкасына батарейалардан кернеу беріледі, нәтижесінде рельстерге 10 тс күшімен тақалады. Жылдамдықтың 15-10 км/сағ –дейін төмендегеннен соң электрлімагнитті тежегіш автоматты түрде қосылады. Дискалы тежегіштер Дискілі тежегіштер тежелу кезінде донғалақтың сырғанау беттерінің қызуын жою үшін жылдамдықты жолаушы поездар вагондарына орнатылады. Тежегіш төрт дисклерден тұрады арбашаға, донғалақтардың өстерінің ішкі бөлігінде қатырылған, және сегіз жұптастырылған ричагтар. Ричагтардың әрбір жұбы тежеу цилиндрлерімен және екі башмактармен шарнирлі байланыстырылған, көлденең балкалармен және кронштейндермен қосылған балкада орнатылған. Тежеу дискалары бүтіндей немесе жинақталатын болып шойыннан жасалынады. Олардың ішінде қабырғасы болады, олардың көмегімен ауа ағыны дискаларды суытады. Тежеу тоқтатылғанда башмактар дискалардан серппелердің көмегімен алып кетіледі.Дискілі тежегіштің әрекетін басқару колодкалы тежегіштермен бірге орындалады.
Тайғанауға қарсы құрылғылар 140 км/сағ және одан жоғары жылдамдықтағы жолаушы поездар донғалақтардың рельстермен ілінісу бойынша шектерінде тежеу күшін тудыруы қажет. Донғалақтардың қысылып қалмауын қамтамасыз ету барысында тайғанауға қарсы құралдар қолданылады. Бұл қондырғылар тайғанай бастаған донғалақты тежей бастайды. Тайғанауға қарсы қондырғыларда донғалақ жұбының лезде айналуының төмендеуінде босататын клапанға белгі беретін өстік датчиктер орналасқан, және босататын клапанның көмегімен тежеу цилиндрлеріндегі ауа тез арада атмосфераға жіберіледі. Тежелген донғалақ бірқалыпты айнала бастайды, және тежеу цилиндрлері қайтадан автоматты түрде сығылған ауамен толтырылады. Осындай түрдегі тайғанауға қарсы қондырғылар келесі негізгі техникалық шарттарға жауап беруі қажет: 2 м/с2 баяулауда қондырғы іске қосылмайды, 4 м/с2 баяулауда олар әрекетке келуі қажет. Инерциялық – механикалық датчиктерге қарағанда электрлік өстік датчиктер екі белгі беріледі. Біріншісі донғалақтың айналу жылдамдығының төмендеуінде, екіншісі донғалақтың айналу жылдамдығы бірқалыптанған соң тежеу цилиндрлерін толтыруға белгі беріледі. Вагонның барлық донғалақ жұптарының қысылуы кезінде шекті баяулаудың абсолютті шамасын реттейтін қондырғы іске қосылып, барлық тежеу цилиндрлерінен ауа жіберіледі.
№19-20 Лекция Тартым мен тартым есептерінің теориясының методологиялық негізі. 1.1 Жалпы түсінік Тартым теориясының негізгі мәселесі пойыз қозғалысының зертеу және есептеу болып табылады. Классикалық механикада және техникалық кибернитикада сондай-ақ жүйе мен дене қозғалысының есебін жүргізеді. Бірақта бөлімінің осы үш туыс салаларының мәселесінің мақсатымен оны шешу әдістерітек қана сабақтас байланысқа емесі сондай-ақ пойыз қозғалысын зерттеу кезіндеескерілетін кейбір ерекшеліктерге ие. Классикалық механикада екі фундаменталды мәселені шешеді: Берілген күштердің әсерімен механикалық жүйені ашатын қозғалысты анықтау (тікелей есеп), қозғалысы берілген жүйеге хабарлауға қабілетті күшті анықтау (кері мәселе). Қозғалысты анықтау - яғни, координатттарымен сипаттайтын, осы уақытта жүйенің күйін анықтау. Берілген мәселені шешуде үлгісі мен өлшемі белгісіз, механикалық жүйені материалдық нүкте немесе өзгертілмейтін жүйе деп аталады. Материалдық нүкте дененің құрылымын ескермец масса қасиетіне ие және механикалық қозғалысын есептеу үшін жеңілдетілген модель болып табылады. Материалдық нүктенің фазалық координата оның үш өлшемді кеңістіктегі орналасуын көрсетеді. Ағымдағы уақытта фазалық координаттың өзгеруін қарапайым дифференциаланды теңдеумен жазады. Егер есептік шарты бойынша күштің, жүйенің массасының мәндері және бастапқы жағдай – қозғалыс басындағы жылдамдықпен координата берілсе, онда диференциялды теңдеуді Коши есебін түрінде қайта интегралдап жүйе қозғалысының заңын ашамыз. Классикалық механикада қозғалысты нағыз түсінікте – уақыт ағымында евклидовтың кеңістіктегі жүйенің жағдайының өзгеруі ретінде түсінеді. Адам жағынан немесе автоматты құрылығы жоқ болғанда жасалынатын мұндай мақсатсыз бағытталған қозғалысты табиғи қозғалыс деп атайды. Техникалық кибернетикада басқарылмайтын қызметті оқытады. Сондықтан адамның тәжірибелік қызметі үшін барлық қызығушылық емес, тек қана мақсатта бағытталған қозғалыс қажет. Кез – келген ұйымдастырылған жүйенің әрқашан да өзі жоспарына жету үшін мақсатты болады. Мұндай жағдайда қозғалыс мақсатының категориясы заң күшіне ие және оны басқарылатын қозғалыс есептерінде қажет. Мақсат ұғымына жүйенің қол жеткізуге қажет арнайы соңғы күйіне немесе нәтижесіне жету үшін талпынысы жатады. Мысалы, машинистің мақсаты А-пункттен Б-пункттіне берілген уақыт кестесі бойынша поезды әкелу. Басқарушы күшті жылжымалы құрам сипатына және қозғалыс жағдайына сәйкес таңдау арқылы ол алдында тұрған мақсатқа жетуді қамтамасыз етеді. Мақсатқа жету талпынысы қозғалысты басқарудың қажеттігін тудырады. Жалпы жағдайда басқару деп, жүйенің бір жағдайдан екінші жағдайға өтуін қамтамассыз ететін жүйеге әсер етушілікті таңдауды айтады. Соның арқасында қойылған мақсатқа қол жетеді. Сырқы ортаның әсмер етуін және істеу сенімділігі мен тұрақтылығы бойынша жіберілген жүйенің күйін есептеу, мұндай іріктеудің міндетті шарты болып табылады. 1 .1 суретте басқарылатын әсер етудің u қайта түрленуінің құрылымдық сұлбасы көрсетілген және мұнда сырқы қоздырушы әсер етулерде ( поезд қозғалысына кеднргілер ) локомативтің тартым күші немесе поездың тежеу күші, жүйенің күйінің параметірлері ( жылдамдық, үдеу, жүрілген жол т.б. ) басқарылатын әсер етулер z. Жүйенің қозғалысы былай қорытындылады: u(t) және z(t) кіретін әсер етулердің ықпалы мен t уақыт ағымында x(t) жүйесінің шығу координатының өзгеру жүреді. Егер жүйе жұмыс істеу процессі түрлі физикалық табиғаттың заңдылығына бағынатын көптеген өзара әсер ететін элементтерден тұратын болса, қозғалысы кеңінен тарау қажет. Уақыт сайын өзара әсер ететін бір тұтас ретінде кибернетикада жүйеден өзара байланысатын элементтер тұтастығы түсінігі қабылданған. Ақпараттар айналымының көлеміне ие. Көптеген өзара байланысқан элементтерден тұратын, сыртқы ортаның кездейсоқ факторларды өткізетін және адамдардың әсер етуін басқаратын жүйені атайды. Жүйенің қозғалысы деп кең түсінікте жүйенің күйінің өзгеруі түсіндіреді: кеңістіктегі орын ауыстыру жүйенің жүрісін зерттеуге қызығушылық көрсететін жылу, ток және басқа параметрлерінің өзгеруі. Жүйенің ауыспалы күйінің ағымдағы уақытта өзгеруін жүйенің бағыты жүріс – тұрысы, бет алысы, мінез құлқы деп атайды.
1.1 -сурет. Баскарылатын әсер етудің (и, - иг) басқару объект /-дін (Х/ — х„) параметрлер күйіне, сыртқы өсерлердің кесірінен (т.\ -' 2т), кайта түрленуінің қүрылымдық сұлбасы.
Бұл жағдайда поездың фазалық координатының түсінігі кеңінен тарайды. Онымен әрбір уақыт сайын қозғалысты алдын – ала болжауға болатын әр түрлі физикалық табиғат күйінің параметрлер жиынын түсіну қажет. Көбіне мұндай параметірлер мыналар болып табылады: поездың тартым учаскесіндегі координаттарымен жылдамдығы, тартым қозғалтқыштарының жүктеме тоғы, тартым генераторының кернеуі, электірлі машина орамасының қызу темперетурасы, дизельдің айналу жиілігі, отын шығыны, доңғалақтың рельспен ілінісу тұрақтылығының көрсеткіштері. Поездың жүріс – түрысы басқарылатын жүйе сияқты анықталады: тасымалдау ТЕЕ (ПТР) бойынша процесінің және оның басқару мақсатымен, сырқы әсер етулермен, жылжымалы құрамның нормативті тартым және тежеу қасиеттерімен машинисттің немесе поездың авто жүргізу жүйесінің жағынан басқарылатын әсер етулермен қозғалыс туралы мәселені мақсат қоюдың, оны шешуге жүйелі қараудың модельдеу әдістерінің әрі қарай дамуының, натурды экспериментінің және қолданбалы математиканың жаңа әдістерін қолданудың арқасында күрделі жүйенің жүріс – тұрысын есептеу және зерттеуге мүмкіндік туды. Қозғалысты басқару теориясында екі негізгі есептер шешліледі – басқарылуы туралы және бақылауы туралы. Басқарылу туралы есепті шешу күштерді басқару анықтамасына сәйкес келеді. Жүйенің ресурстарын және белгіленген шектеулерді ескеріп берілген күйден соңғыға әкелуі мүмкін. Бақылану туралы есепті шығару ұозғалыстың дифференциялды теңдеуін интегралдаудың әрбір қадамында бақылауға болатын координаттар бойынша жүйенің күйінің фазалық координатын анықтауға сәйкес келеді. Қозғалысты және шектеу күйінің параметрлері болжау бақылануы туралы есепті көрсетеді. Бақылану әдісі поезд тартымы теориясында кең қолданылады. Поезд тартымы теориясында екі негізгі есептер шешіледі: 1) Сериясы берілген локоматив тартым мен қозғалыс жылдамдығының нормативті параметрлерін бақылау кезінде жолдың пішіні берілген учаскеде көтере алатын поезд массасын анықтау керек; 2) Берілген тартым учасксінде басқарылатын қозғалыс массасы берілген поезд үшін анықтау қажет, огымен нормативті және шектеулі жағдайды сақтауда қойылған мақсатқа қол жеткізуге мүмкіндік туғызар еді. Классикалық механиканың, кибернетиканың есебін және поездар тартымы теориясын зеттеу мен шешудің жалпы методологиялық амалы болып модельдеу табылады. Бұл олардың арасындағы ажырамас байланысты анықтайды. Олардың айырмашылығы құбылыстар мен процесстердің физикалық табиғатымен, жүйенің тағайындалуымен, оларды зерттеу мақсатымен, бастапқы және ағымдағы аппараттың болуымен, шектеу жағдайымен, матеметикалық формулануымен және болжаудың қажетті нақтылығымен анықталады. Классикалық механикада, қарапайым механикалық қозғалысты қарастырады; фазалық координаттар жылдамдықпен және уақыт сайын жүйенің орналасмуымен, демек, жүйе екі параметрлері; мұдай жүйеқозғалысының метеметикалық моделі материалды нүкте қозғалысының дифференциялды теңдеуін көрсетеді; күштер берілген, уақытқа тәкелді емес және басқарылатын болып саналмайды, қозғалыс – табиғи (естественное); жүйеге тек еркін дәреже санын анықтайтын түйіспе – механикалық байланыс әсер етеді; жүйенің жүріс – тұрысы энергияны сақтау және классикалық механика теоремасына бағынады. Басқарылатын қозғалыс теоремасмында және поездар тартымы теориясында қозғалыс кең өрісте қарастырылады; жүйе күйінің фазалық координаттары әрбір уақыт сайын көптеген параметрлермен анықталады, қозғалыс – басқарылатын; жүйенің жүріс – тұрысын жазуды бірнеше математикалық модельдермен жүргізіледі. Айтылғандардан былай қорытындылауға болады: жүйе қозғалысын есептеуге кіріспестен бұрын, зерттеуші мақсатты, есеп қоюды, қозғалыс моделін құру және зерттеу әдістерін нақты анықтау қажет. Техникалық кибернетика поезд тартымы теориясынаан біраз артта құрылғанына қарамастан есепті шешудің принциптерінде және тәсілінде олардың арасында көптеген ортақтық байқалады. Ғылыми – техникалық прогрессті айтарлықтай шамада анықтайтын басқару туралы фундаменталды ғаламмен кибернетика бекітілуіне байланысты, ал пойыздар қозғалысын басқару темір жол көлігін басқарудың автоматтандырылған жүйесінің құрамдық бөлігі болу қажет, негізін құрайтын принциптерді, кибернетика түсінігі мен әдістерін пойыздар тартымы курсында қолдану мақсатқа лайық. 1.2. Пойыздың басқарылатын қозғалысы туралы есепті қою және оны шешуге жүйелі қарау Пойыз қозғалысын есептеу үшін құрам массасы, локомотив сериясы, тежеу құралдар, жол пішіні, темір жол бойында станцияның орналасуы берілуі керек. Механикалық қозғалысты және жылжымалы құрам күйінің параметрлерінін анықтау қажет. Бұл параметрлер локомотив жұмысының сенімділігін және қауіпсіздік жағдайын сақтаудағы қойылған мақсатқа қол жеткізеді. Қойылған есепте белгілі бір мақсатпен жүретін күрделі жүйенің басқарылатын қозғалысы туралы айтылған. Күрднлі жүйе қолзғалысы есебінің мақсатын анықтау және әдісін тиаңдау үшін жүйелі қарау кеңінен қолданылады, жүйенің жүріс-тұрысын зерттеу үшін жүйенің әр түрлі элемнттерінің өзара байланысын ескеру жүйелі қараудың мәні болып табылады. Өзара байланыс элементтердің қарапайым механикалық тұтастығы сияқты емес, мақсатқа қол жеткізудегі олардың өзара әрекетінің бір тұтастығындай қарастырылуы керек. Демек, пойызды автономды жүйедей емес, темір жол жүйесіндей буын ретінде, ал оның қозғалысын тасымалдаудың технологиялық процессінің бір бөлігі ретінде қарастырамыз. Жүйелі қарауға сәйкес пойыз қозғалысының мақсаты жол мақсатты қызметінен анықталуы қажет, оған темір жолдың оң үлкен өткізгіштік және алып жүргізушілікті пойыз қозғалысының массасы мен жылдамдығын жоғарылату жолымен қамтамасыз етеді. Әлбетте, қозғалысты басқару және басқа есептер тізбектеліп жүруі мүмкін, бірақ, олардың барлығы негізгі мақсат шегінде шешілуі қажет. Жүйенің жүріс-тұрысын және күшін басқару жолымен мақсатқа қол жеткізуге болады. Осы жолмен пойыз қозғалысы табиғи қозғалыстан қароағанда мақсатқа бағытталған болып табылады. Пойыз теміржол жүйесіндегі элемент болғандықтан, оның қозғалысын басқару тұтас қызметке, тасымалдау технологиясына және қозғалысын график бойынша ұйымдастыруғабағынады. Мақсатқа жету жету дәрежесі болып пойыздың басқарылатын қозғалысының оңтайлығы шамасы қызмет етеді. Мұндай шама болып пойыз қозғалысының қабылданған ұйымдастыруда және берілген техникада теміржолдың және стансаның өткізгіштік пен алып жүрушілік қабілеті деңгейі табылады. Оңтайлы қозғалысқа жетуге ұмтылу локомотив пен вагонның жұмыс сенімділігі және қозғалыс қауіпсіздігінің жағдайы бойынша жіберілітіндерден және пойыз ресурсында мүмкін шектерден шықпауы керек. Ол үшін тартым есептеріне сенімділік бойынша шектеулердің, тежеулердің және тартымның нормативті параметрлері белгіленген. Объектінің күйі мен жүріс-тұрысы туралы ақпаратсыз кез келген басқару мүмкін емес болғандықтан, темір жолдың барлық торабында пойыз қозғалысын есептеу үшін нігізгі ақпарат ретінде жылжымалы құрамның біртұтас паспорттың сипаттамалары белгіленген. Әр түрлі жолдардың нақты пайдалану жағдайында натуралды эксперимент – сараптама пойыз қозғалысы параметрлері туралы ең құнды ақпарат беріледі, сондықтан реттеу үшін тартым есептері және интенсификациясы резервтері мен тартым үнемділігін іздеулер қолданылады. Физикалық табиғаты әр түрлі, өзара ететін көптеген элементтердің (дизель, тартым берілісі, экипаж, вагондар, жол, СЦБ және байланыс т.б) мақсатқа бағытталған қозғалысқа қатысуы, сондай-ақ, адамдарды қандайда бір физикалық заңда нігізделген, күрделі жүйенің қозғалысын матеметикалық жазу қиындатады. Мұндай күрделі есепті шығару үшін математикалық модельдеу қолданылады [25;28;38;]. Әр түрлі процесстегі математикалық модельді құруда және зерттеуде жеңілдететін болжамдар мен олардың арасындағы арнайы қатынастар мақсатқа бағытталған қозғалыстың есебін жалпы шешуді табуға мүмкіндік береді. Мақсат қызметі, жүйелі қарау және математикалық модельдеу пойыз қозғалысын зерттеуде, болжауда негіз қалаушыұстанымдар болып табылады. 1.3. Пойыз тартымы мен қозғалысын математикамен модельдеу Кез-келген процесстер кеңістікте және уақытпен жүреді сондықтан жүйенің жүріс-тұрысы ағымды уақыт қызметінде күйдің фазалық координатының өзгеруімен анықталады. Жүйенің жүріс тұрысы оның күйінің уақытына тарихи сияқты қарастырылады және қарапайым дифференциалды теңдеумен жазылады. Алты еркін дәрежелісі бар еркін дене үшін классикалық механикадағы алты дифференциялды тікте көрсетіледі. Егер жүйе өз ара байланысқан н денелерден түратын болса онда оның қозғалысын жазу үшін н есе үлкен теңдеу қазет. Егер поезд құрамындағы әрбір вагонның жүріс – тұрысын жазуға талпынса мұндай есеп ЭВМ – нің өзінде шешіле алмайды. Поездың жүріс – тұрысын жазу былай күрделінеді: механикалық, термодинамикалық, электромагниттік және басқа дифференциялды теңдеу оның параметрлері көптеген факторларға түзу емес тәуелділікке ие оны әрдайым өлшеу мүмкін емес, сондай – ақ оларды интегралдаудың белгісіздігін анықталмауын және мүмкін еместігін тудырады. Эксперименттер осы процеске мол сенімділікпен тек маңызды фокторларды есептеп шығаруға болатындығын көрсетті. Мұндай ыңғай модельдеу теориясына әкелді. Процесті түбегейлі талдап сипаттаудан оларды модельдеуге көшуі күрделі жүйенің жүріс – тұрысын зерттеу мен болжаудың ең жалпы әдісі болды. Қозғалысты басқару теориясында күрделі жүйенің жүріс – тұрысын зерттеудің методологиясын анықтайтын негізгі түсінік болып табылады. Математикалық модель деп шегінде зерттелетін процестер параметрлерінің есептеу процедурасы негізінде түп нұсқасының жүріс - тұрысы туралы қажетті ақпаратты беретін жуықтаудың алынған дәрежесі математикалық қатынастар жүйесін айтады. Математикалық қатынас бастапқы шарты дифференциялды теңдеуді және шектеуді көрсетеді. Есептеу процедурасына оңайлататын болжамдар мен теңдеулер жатады. Модель білімнің нақты саласы талабымен әрдайым байланысты болғандықтан, ол тен зерттеу мақсатына қызығушының тудыратын процестер мен ерекшеліктерді көрсету керек. Күрделі көп параметрлі жүйеде физикалық табиғаты әртүрлі және барлық жүйенің жүріс – тұрысына қатысы бар процестер бір уақытта жүруі мүмкін болғандықтан, біртұтас математикалық модельді құру мүмкін емес. Мұндай жағдайда жеке процестерді көрсететін бірнеше модельдерді құрады. Бір обьектінің мұндай модельдері өзара белгілі бір қатынаста болады. Бір модельді құру қорытындысының, екіншісін құру үшін қолданады. Мысалы алғашқы тартым есебінде механикалық қозғалыстың моделі құрылады V(S) оның негізінде жүрілген жолға қозғалыс уақытына тартым генераторының немесе электрлі қозғалтқышы жолына және олардың орамасының қызуына, механикалық жұмысқа, поезд тартымына кететін отын шығынына жылдамдықтың тәуелділік моделін құрайды және зерттейді. Математикалық модельдерді құру және түп нұсқасының жүріс – тұрысын сыртқы ортаны модельді шешу қорытындысы бойынша зерттеу процедураларын математикалық модельдеу деп атайды. Оның негізіне процесс сипаттайтын теңдеудің теңдігі (аналогия) және айнымалы түп нұсқа мен модель арасындағы қатынастың бір қатарлығы жатады. Математикалық модельдеу әдісінің дамуы ғылыми бағытты жасауға әкелді-теңестіру (идентификация) теориясы. Нақтылы жүйенің жүріс – тұрысы ретінде өзгеруін бақылай отырып жасауға болады. Тек кіру және шығу параметрлері бақылауға болатын, ал ішкі құрылысы мен процесстің белгісі болып қалатын шартты жүйе қара жәшәк атағын алуы (40,28,23). Қара жәшік әдісін қолдану жүйенің сыртқы параметрлерінің өзгеруі бойынша жүріс – тұрысын алдын ала болжауға болады. Бұл жағдайда қозғалыс есебі біршама жеңілдетіледі, сондықтан қара жәшік әдісі кеңестіру теориясыеда негізгі алынатындар табылуы және қызығушының жүйенің құрылыуына емес, оның жүріс – тұрысына туатын күрделі басқаратын жүйені модельдеу кеңінен таралды. Поездар тартымы теориясында қара жәшік әдісі кеңінен қолданылады. Мысалы, механикалық қозғалыцсты есептеу үшін тарту күшін немесе тежеу күшін есептеуге болады, ал сыртқы әсерлер деп – қозғалыс кедергілерін, ал шығу деп – жылдамдық пен жүрілген жол. Сонда ғана энергияның түрлену, дизель ішіндегі күштің тарт у берілісінің, тежеу жүйесінің көмекші агрегаттардың күшінің пайда болуы процестерінің модельдерін құру қажеттілігі жоқ. Пойыз тартымы мен қозғалысы процессін модельдеу келесі тізбектікпен жүргізіледі: 1) ауызша-жазбаша моделін қүру; 2) оның негізінде қозғалыс заңын аныктайтын математикалық модельді қүру; 3) пойыздың шекті күйі шегінде мақсатқа жетуге бағытталған модельді зерттеу; 4) туп нүсқаға барабар анықтайтын натурды эксеримент; 5) модельді зерттеу қорытындыларын реттеу және шешім қабылдау. 1.4 Пойыз тартым мен козғалысыныц ауызша-жазба модельдерін қүру Ауызша-жазба модель күрделі жүйенің қүрылымы, касиеті, күйі мен жүріс-түрысы туралы жеткілікті негізделген болжамдар зацы жинағын керсетеді. Бүл модель жүйенің күйін және жүріс-түрысын болжауға қажетті математикалық модельді қүрудың ақиараттық негізі болып табылады. Ауызша жазба моделін қүруда алдымен жүйенің жағайындалуын, күрылымын және зерттеу мақсатын, оның күйі мен жүріс-түрысын анықтайтын физикапық зацдарды, жүйе туралы негізгі ақпараттардың болуын жөне оның сыртқы ортамен өзара әсерін белгілейді. Одан кейін жүйе бөліктерінің өзара өрекетінің жоне сыртқы ортаның осершің ең маңызды парметрлерін ресурс сенімділігі жене байланыс үстайтын шектеулерді шығарады және сөзбен жазады; жүйенің жүріс-тұрысын математикалық түрде жазуға мүмкіндік тудыратын, жеңілдетілген болжамдарды делелдейді; есептін нақтылығымен дүрыстығы дәрежесін белгілейді. Жүйенің физикалық зацдарды мен оның белгіленуі өндірістік процесстің мағынасымен жөне табиғатымен анықталады. Темір жол көлігінін, өндірістік прцессінің маңызыдылыгьш К. Маркс аныктады: «Адамдар мен тауарлар арнайы көлік күрылымен бірге жүреді, қозғалыс келік күралымен, онын орын ауыструы өзі тудыратын ондіріс процессі болады». Сондықтан, пойыз козғалысы мен тартылатымының базалық моделін күру үшін классикалық механикалық заңдардын параметрлерді (тоқ, тартым машинасының кернеуі, олардың орамасыньщ қызу температурасы және т.б.) тиісті математикалық модельдерді күрумен аныктайды. Сонымен бірге тартым режимін анықтайтын базалық модель және осы модеьдердін физикалық заңдары қолданылады. Ауызша-жазба моделін қүру нөтежиесіиде алынатын (шығатын) болжамдар негіз болып табылады, оған сейкес жүйенің жүріс-түрысының математикалық сипатталуын жүргізеді. Пойыздар тартымы теориясында келесі болжамдар қабылданды: I болжам. Пойыздыц механикальщ цозгалысыи бір еркін дәрежесі бар математжалық түрде сипаттауга бопады. Жүйенің еркін дәреже саны байланысты үстайтындармен анықталуы. Пойыз үшін оның мақсатқа бағытталған қозғалысының еркін дөрежесін анықтайтын байланыстарды ғана ескерген жеткілікті. Байланыс болып авто ілінісу қүрылғысы мен рельстер табылады. Авто ілінісу қүрылғысы локомотивпен ваондарды бірқалыпты жылдамдықпен және удеумен жүргізуіп камтамасыз ететін ішкі байланыс үстау рөлін атқарады. Егер, мақсатка бағытталған қозғалысты ғана ескеріп, жылжымалы қүрамның тербелмелі қозгалысы мен өзара орын ауыстыруын ескермесек, онда, есепте пойыз өлшемін ескермеуге болады жөне оның қозғалысын өзгермейтін жүйенің үдемелі қозғалысы деп қарастырады. Классикалық механикада мүндай қозғалыс математикалық түрде жүйенің түтастай қозғалысы - деп сипатталады, яғни жүйенің барлык массасы оның орталығындағы материалдық шығарылған нүкте. Тартым есептерінде пойыз қозғалсын, пойыз ортасына ораласқан материалдык нүктенің қозғалысы ретінде сипаттайды. Рельстер сыртқы байланыс үстау релін атқарады. Бүл байланыс пойызды бір бағытга қозгалуын қамтамасыз етеді (рельс бойы); демек, пойыз еркін бір дәрежесі бар. Еркін бір дәрежесі бар материалды иүктенін қозғалысын сипаттау үшін бір дифферениналды теңдеу жеткілікті. Сондықтан, пойыздың мақсаты бағытталған қозғалысы бір еркін дережесі бар материалды нүктенің қозғалысы ретінде бір дифференциалды теңдеуменен жазуға болады. Бүл тартым есебін ондйлатады, бірақ кейбір қате жіберрушілік болады.II болжам. Пойыз қозгалысыи алдын-ала болжау үшін тек сырпщы күштерді есептеген жеткілікті, сыртқы куштер мацсапща багытталган қозгалысты аньщтаііды жоне оның багытымен сөйкес кечгді. Өзгермейтін жүйенің ішкі күштерінің жүмысы нөлге тең, себебі, күштер өзара теңеледі; демек оларды қозғалысты математикалық сипаттауда ескермеуге болады. Тартым есебінде тек пойыз қозғалысының бағытымен сөйкес келетін сыртқы күштері есептейді (коллинеарлы күштер). Егер, коллинеарлы күштер бір нүктеге түсіріген болса, онда оларды алгебралық қосуға және қозғалыс жылдамдығын қорытынды күштің әрекетімен карастыруға болады. Пойыз қозғалысын аыктайтын сыртқы күштер санына тартым күшті, козғалысқа келтірілетін кедергі күші және тежеу күші жатады. Есеп қолайлы болу үшін бүл күштерді локомотив пен вагондар донғалағының тығынына түсірілді. Қорытынды күшті пойыздың 1 т массасынына келтіреді жене оны меншікті деп айтады. Ш болжам. Жүйе ішіндегі процесстер динамикасыи есептемей, жүйеиің кіруі мен шыгуы бойынша цозгалысты алдын-ала болжау мүмкун, онымеи тартым, тежеу және цозгалыс кедергісі күштеріиің статикальщ сипатамаларын тартым есептерінде колдануга мүмкүядік береді. Күштердің сипатамасын қүрылғылық жүмысы түрақты болған жоне қозғалыстың жылдамдығы бір калыпты болған стационарлы жагдайда өткізілетін тожіребилер қорытындысы бойынша түрғызады. Басқару режимін нсмесе сыртқы жүктемені ауыстырғанда күпітің өзгерілуін белгіленген бір процесстен екіншісіне өткенде ескермейді. Мүндай сипаттаманы статикалық деп атайды. Пайдалануда динамикалық процесстер басым, сондықтан өту процесстерінін уақытын ескерген жөн. Бірақта типтік динамикалық сипаттамаларды жол желісі үшін күру оту процесстерінің күрделі физикалык табиғатынан және олардың ор жергілікті, әртүрлі жағдайда және пойыз қозғалысын үйымдастыруға төуелділігінен мүмкүн емес. Сондықтан тартым есебінде статикалық сипаттаманьі жалпы желілік априорды ақпарат ретінде колдануға тура келеді. Егер жүйе козғалысы есебінде қара жәшік өдісіп және кибернетика мен классикалық механикада қабылданған кдшыктан әсер ету принцибін қолдансак; онда динамикалық жүйенін, қозғалысын есешеуге статикалық сипаттамаларды кейбір қателіктермен қолдануға болады. Осы негізінде пойызды қара жөшік деті кабылдаймыз және кіру параметрлерінің езгеруін бакылап (қозғалыс кедсргісі. тартым жөне тежеу күштері), шығу параметрлерінің жүрілген жол мен қозғалыс жылдамдығы езгеруі бойынша оның жүріс-түрысын ету процессін есептемей анықтайтын боламыз. Қашықтықтан әсер ету принцибіне сөйкес былай болжауга болады: белгіленген бір қозғалыстан екіншісіне өтуде күштің ...езде езгеруі болады жөне станционарлы емес (түраксыз) жағдайда қозғалысты болжау үшін сгатикалық сипаттаманы қолдану мумкіндігі туады. Машинистің тежеу кранының түткасы мен бақылаушысы позициясын ауыстыруда немесе тіктігі әртүрлі пішін элементтерінің шегінен пойыздың орталык массасы еткенде бір қалыпты күштің бірқалыпсыз өзгеруін шартты түрде кабылдайды. IV болжам. Тартым есебін оңайлату үшін пойыз күшінің үздіксіз сызықты емес функцшсының тілімді қагідық - сызықты аппроксимацыясы жіберіпеді. Ол теңдеуді Коши есебі турінде шешуге мумкіндік береді. Егер, жүйеге әсер ететін күштердің бірі жылдамдыққа төуелді болса, онда оның козғалысы туралы есепті тек козғалыстың дсфференциалды суперпозиция принцибін қолдану мүмкіндігі туу үшін қозгалыс сызықты болу керек (жүйенің қорытындылайтын қозғалыс әрбір күштіц жеке өсерімен туатын қозғалыстар соншамасына тец). Біракта, жүйснің қозғалысын анықтайтын күш функциясы түзу емес, сондыктан күрделі сызықты емес дифференциалды теңдеуді шешуді кажет стеді жөне жүйенің қасиеті оньщ жүріс-түрысына төуелді, демек мүнда суперпозиция прицибін колдануға болмайды. Ол үшін шекті жерде жол берілген шекте сызықты емес фупкцияга сызыкты етуді (линеаризациялау) жүргізеді, суперпозиция принцибін қолданады жөне дифференциалды теңдеуді Коши есебі үлгісінде шешеді. Аз ауытқу принцибі бойынша кванттау әдісімен линеаризацияны жүргізеді. Тең әсер ету күштерінің үздіксіз сызықты емес функциясып қозкалыстың жылдамдығының аз интервалы бойьшша дискретті (үздікті) тілімді -сызықтымен ауыстырады. Сонда ғана, әрбір интервал шегінде күшті түрақты деп, және интервалды тиісті орташа жылдамдықты қабылдауға болады. Бүл физикалык көзқарасқа тең, яғни бір калыпсыз баяулатынған қозғалысты бір қалыпты үдеумен ауыстырады. Мүндай мүмкіндік есепте шамалы қателік жібереді, ойткені пойыз массасының түрақты уақыты локомотив пен қүрамнын қуатты энергиялы қүрылғысының түрақты уакытынан жоғары. ВНИИЖТ өдісімен уақыт интервалы бойынша тежеу есебін шешетін болсақ, уақыт факторын тежеу өсерінде біршама нақты " есептеуге болады. Үздікті - сызықты фуикциясы жылдамдық интервалы аз болган сайын, негізгіге жақын келеді. Оны күруды аппроксимация (жакындау) деп атайды. ТЕЕ (ПТР) нормативі бойынша апроксимация 10 км/сағ кем емес жылдамдық интервалымен шектеледі. Осыдан барып, пойыздың ауызша-жазба моделін күру үшін оны бір еркін дәрежесі бар өзгермейтін жүйе деп есептеуге болады. Бір дорежесі бар өзгермейтін жүйеге пойыз узындығы ортасындағы массасын келтіретін сыртқы күштср есер етеді және ол пойыз қозғалысының бағытымен сәйкес келеді (немесе оның бағытымен қарама-қарсы). Егер күштер жылдамдыққа төуелді болса, онда қозғалысты дифференциалды теңдеуді шешу жолымен ғана болжауға болады. Бүл еркін дөрежесі бар пойызға бір дифференциалды гендеудің озі жетеді. Күрделі жүйенің жүріс-түрысын есептеу үшін кара жөшік өдісін қолданады. Қара жәшік әдісі жылдамдығы аз интервалды априонды ақпарат ретінде статикалық сипаттамаларды қолдануга мүмкүндік береді. Күштер сызықты болмағандықтап, сызыкты емес дифференциялды теңдеуді шешү қиын. Пойыз моделін қүру үшін статикалык сипаттаманы үзінді-сызықты аппроксимациялауды жүргізуге жөне қозғалыстың дифференциялды теңдеудің Коши есебі үлгісінде шешуде суперпозиция принцибін қолдануға мүмкіндік беретін ауытқуы аз пршщипті қолданады. Жылдамдықтың өрбір интервалында қозғалыстың берілген режиміне және интервалда орташа арифметикалық жылдамдыкка сәйкес келетін мән бойьгнша түрақты тең өсер ететін күшті қабылдауға болады. Күштің байланысына қарай қозғалыс режимі келесідей бөлінеді: 1) Тартым - локомотивтің тартым күші Ғк және қозгалыс кедергісінің 2) Бос жүріс — бір күш әсер етеді 1¥к; 3) Тежеу - 1¥к күші мен тежеу күші Вт өсер етеді. Режимдер ауысқанда немесе сыртқы жүктемеде узақтан всер ету принцибіне сойкес тең әсер ететіп күштердің секірмелі (скачкообразный) езгеруі болуы мүмкін. Тең өсер етуді қүрайтын күштердің қатынасына қарай пойыз қозғалысының сипаты анықталады. Мысалы, үдемелі қозгалыс - егер, тартым күші қозғалыс кедергісі күшінен үлкен, баяулатылған - тартым күші кедергі күшінен аз, бірқалыпты олар езара тең. Пойыздың түрақтылық қасиеті бар, сондықтан ол өрқашанда кез-келген қозғалыс режимінде тең шамалы жылдамдыққа талпынады. 1.5. Пойыз қозғалысы мен тартымының математикалық моделін құру Пойыз қозғалысын дифференциалды теңдеудің ауызша-жазба моделі ескеріліген қорытындысы математикалық модельді құруды көрсетеді. Ол үшін жүйенің кинетикалық энергиясының өзгеруі туралы теореманы қолданамыз. Жүйенің кинетикалық энергиясы классикалық механикада келесі түрде қалыптасады: механикалық жүйенің кинетикалық энергиясының өзгеруі оның кейбір орын ауыстыруында осы орын ауыстырудағы ішкі және сыртқы күш жұмысының алгебралық қосындысына тең. 1 болжамға сәйкес, пойыздың ішкі күшінің жұмысы нөлге тең, сондықтан оны ескермейміз. Сонда, энергияны сақтау заңына сәйкес: dТ= (Ғк- мұндағы:T - пойыздың кинетикалық энергиясы, кг Жолдың және жылдамдығы аздап өсірілуі шегінде күшті тұрақты деп қабылдайды, сондықтан оларды дифференциалды түрде көрсетпеуге де болады. Вт жөне >Ғк күштерін теріс мәнімен қабылдайды, өйткені олар пойыз қозғалысына кері бағытталған. Пойыздың тек үдемелі козғалыстан басқа тартым электрлі қозғалтқыштың тісті берілісінің, жәкірдің және қос доңғалақтың айналмалы қозғалысына ие екендігін ескереміз. Сондықтан Кениг теоремасын қолданған жөн: өзгермейтін механикалық жүйенің кинетикалық энергиясы жүйенің орталықты массасы жылдамдығымен және инерция орталығы айналасындағы айналмалы козғалыстың кинетикалық энергиясымен бірге барлық массасымен үдемелі қозғалысының кинетикалық энергиясының қосындысына тең. Егер пойыз түзу бойымен қозғалса, онда оның инерция орталығы айналасындағы айналуын ескермеуге де болады. Тек жүйенің жеке бөліктері өздерінің инерция орталығының айналасындағы айналуын есептеу қажет. Пойызға Кениг теоремасын былай қалыптастыруға болады: пойыздың кинетикалық энергиясы пойыз ұзындығының ортасында орналасқан инерция орталығындағы пойыздың барлық массасының жылдамдықпен үдемелі қозғалысты кинетикалық энергиясының соммасына және тісті берілістің, қозғалтқыш жәкірінің және қос доңғалақтың өздерінің инерция орталығында айналуының кинетикалық энергиясының соммасына тең. Мұнда пойыздың кинетикалық энергиясы келесі формулаларымен анықталады: T=m мұндағы: т — пойыз массасы, v - пойыздың үдемелі қозғалысының жылдамдығы, км/сағ; Iкв, Іkl, Ія - вагон мен локомотивтің тартым қозғалтқышының жәкірінің тиісті инерциясының полярлы моменттері; wкв, wкl wя вагон мен локомотивтің тартым қозғалтқышы жәкірінің тиісті бұрыштық жылдамдығы. Тартым есебі ыңғайлы болу үшін айналмалы массаны үдемелі қозғалысқа келтіруді жүргіземіз. Қозғалысқа келтіру буын етіп пойыз доңғалағын қабылдаймыз. Жүйенің айналмалы массасының және келтірілген массаның эквиваленттілік шарты болып олардың кинетикалық энергиясының теңдігі табылатындығыны белгілі. Осы негізде былай жазамыз:
мұндағы: т пойыз массасы, ол үдемелі қозғалысқа келтірілген. Айналатын масса инерциясының полярлы моменттерін анықтаймыз:
мұндағы: ткв, mкl,, тя - вагонның, локомотивтің айналатын қос доңғалақтарының және тиісті берілісті тартым электрлі қозғалтқыш жәкірінің тиісті массалары. Локомотив пен вагонның доңғалақтар радиусын тиісті: Яkв, Якl, деп белгілейміз, ал қозғалтқыштың тиісті берілісінің беріліс санын Бұрыштық жылдамдықты үдемелі қозғалыстың жылдамдығы арқылы көрсетеміз: Онда, (1.3) өрнекке қойғаннан кейін келесі өрнекті табамыз:
Қысқартқанан кейін:
Айналатын бөліктердің келтірілген массасын твр белгісімен белгілейміз, сонда келтірілген масса тп = т + твр . Есепті оңайлату үшін твр /m = ү қатынасын жүргіземіз, сонда тn =т(1 + m(1+ ds = vdt m =
Алынған қатынастың физикалық шамасының өлшеміне көңіл аударайық. Өйткені физикалық шаманың өлшем бірлігі көлікте және халыкаралық жүйеде (СИ) кейбір ерекшеліктерге тән. Өлшем жүйесінде масса кг-мен өлшенеді, арақашықты - м-мен, уақыт-секундамен, жылдамдық — м/с-мен, үдеу - м/сг, күш - Н-мен, көлікте пойыз массасы - т; пойыз жүретін жол - км; уақыт - сағ; жылдамдық - км/сағ; үдеу - км/сағ2. Көгеренттік (сәйкес келуші) ережесін сақтау үшін өлшем бірлігін сандық сәйкес келуін жүргіземіз. Мынаны ескереміз: 1Н күші = 1кг*м/ ал ( 1000 саг
Белгілейік: 12,96/(1+
(1.6) тендеуі пойыздың механикалық қозғалыс заның әрбір уақытта, басқаратын және ауытқуатын күштер, айналайын масса инерциясы ескерілген үдеу мен масса арасында болатын қатынаста көрсетеді. Жол мен жылдамдықтың фазалық координаттарын берілгенде ол пойыздың механикалық күйін анықтайды және оның әрі қозғалуын білуге мүмкіндік береді. (1.6) теңдеу тартым режиміндегі пойыз қозғалысының математикалық моделін көрсетеді. Тежеу режимінде (1.6) теңдеуі былай өрнектеледі:
бос жүріс режимінде
4 параметрінің физикалық табиғатын білу үшін меншікті бірдей әсер ету күшін бірге теңестіреміз Егер Отандық жылжымалы құрам үшін анықталғандар: төрт ості жүктелген вагондарға Тартым есебін оңайлату үшін орта мәні қабылданған: Пойыз қозғалысының қорытынды теңдеуді жалпы түрде көрсетуге болады: Есеп қолайлы болу үшін (1.9) теңдеудің интегралдау арқылы пойыздың қозғалыс жылдамдығын, жүрген жолын және кеткен уақытты, тәжіребилік мақсатта қолданылатын сандық мәндерді анықтайды. Тәжіребилік мақсат - темір жолының тасымалдау процесін жоспарлауда, ұйымдастыруда және технологиясында бірінші роль атқаратын жол торабында пойыз қозғалысы кестесінің құрылуы мен қалыптастыру жоспарының әзірлемелері. Бұл теңдеуді интегралдау үшін пайдалану жағдайында пойыздың күші мен жүріс-тұрысын анықтайтын факторларды білу қажет. Осы мақсатпен қозғалысты анықтайтын -Fk, Вт, Wk күштердің тәуелділігін оқып білу қажет. №21-22 Лекция Локомотивтің тартым күші. Локомотив тартымының негізгі заңы 2.1. Локомотивтің тартым күші мен ілгермелі қозғалысын тудыру механизмі Пойыздың қозғалыс жылдамдыгы мен тартым күші - темір жол жұмысының маңызды параметрлері. Бұл параметрлермен тартым учаскесінің өткізгіштік және тасымалдаушылық қабілетін, локомотивтің өнімділіктігі мен үнемділігін анықтайды. Пойыз массасының нормасы және оның қозғалысының жылдамдығы локомотивтің жанама тартым күшінің, есептеме жылдамдығының ирнормативті - есептеме мәндерімен және тартым сипаттамасымен Ғk(v) анықталады. Бірақ, жанама тартым күшін тура өлшеумен анықтау қиын, сондықтан оны жанама өлшеу әдісімен анықтайды: локомотивке тіркелетін вагон-зертхана динамометрмен. Локомотив авто тіркемесіндегі пайдалы тартым күші
Ол үшін Ғп мен Ғъ күштерінің туу механизмі және схема бойынша тартым қозғалтқышынын айналу моментігінің тізбекте тәртіпте тартым электрлі қозғалтқышы - жетектің тісті берілісі - локомотивтің қозғалатын қос доңғалағы - локомотив рамасы - локомотивтің авто ілінісуі - локомотивке бірінші болып тіркелетін вагонның авто ілінісуі туралы ұғым қажет. Қорытындыны оңайлату үшін келесі пікірлерге (болжамдарға) сүйенеміз: пойыз тұрақты жылдамдықпен түзу көлденең жол бойымен қозғалады, доңғалақтың рельс бойымен тербелеуі материалдың деформациясыз және сырғанаусыз абсолютті қатты дене ретінде жүреді; тісті берілісі - түзу тісті; шестерня мен тісті доңғалақ тартым қозғалтқыш білігіне және қос доңғалақ осіне тегісінше қатты отырғызылған. Локомотивтің қозғалатын қос доңғалағының, тісті берілістің және қозғалтқыш жәкірінің инерциясын; қозғалатын осьтер арасындағы жүктемелі, рессорланған массасының тербелуінен болатын динамикалық жүктемені, энергияны диссипативті күштермен жойылу және т.б. қайта болуді ескермейміз. Бұл құбылыстарды теорияда ескеру күрделі, айқын емес және бұл жағдайда қажеті шамалы. Өйткені олар пайдалы тартым күші шамасына Ғп жиынтықпен бейнеленеді. Айталық берілгендер: қос доңғалақтан рельске түсетін жүктеменің тұрақты мәні П; тиісті берілістің беріліс саны µ; тартым қозғалтқыш білігіндегі айналу моменті индексті тісті доңғалақты шестерняның радиустары r; қозғалаты доңғалақтың радиусы Шестерня 1 тісті доңғалаққа 2 айналу моменті тістер арасындағы үйкеліс шығынын ескеріліп беріледі: Мі=Мdп, мұндағы п - тісті берілістің ПӘК (2.1, а сурет) Тістердің өзара әсер етуі ілінісу бойымен п -п жүреді, ілінісу шестерня радиусы rв1 мен тісті доңғалақ радиусының rв2 < |




 - Вт)ds (1.1)
- Вт)ds (1.1) ; Ғк - локомотивтің жанама тартым күші, Н;
; Ғк - локомотивтің жанама тартым күші, Н;  (1-2)
(1-2)


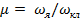 белгілейміз.
белгілейміз.




 ), ал пойыздың кинетикалық энергиясы: Т=m(1+
), ал пойыздың кинетикалық энергиясы: Т=m(1+  )
)  /2. 1 +
/2. 1 +  )ds (1.4)
)ds (1.4) ауыстыруды жүргіземіз. Мұндағы
ауыстыруды жүргіземіз. Мұндағы  ,- құрам мен локомотив массасы, т. Осыдан барып (
,- құрам мен локомотив массасы, т. Осыдан барып (  ) және қысқартқаннан кейін: (
) және қысқартқаннан кейін: (  ) немесе
) немесе (1.5)
(1.5)
 =12.96
=12.96 
 (
(  ) Н/т. Осыдан, дифференциалды теңдеу былай жазылады:
) Н/т. Осыдан, дифференциалды теңдеу былай жазылады: (1-6)
(1-6) (1.7)
(1.7) (1.8)
(1.8) , демек, пойыздың массасының әрбір тоннасына 1 Н үдету күші әсер ететін үдетуді
, демек, пойыздың массасының әрбір тоннасына 1 Н үдету күші әсер ететін үдетуді  көрсетеді.
көрсетеді. = 12,96 (1 +
= 12,96 (1 +  мәнін өлшейді және онымен жанама тартым күші мәнін есептейді.
мәнін өлшейді және онымен жанама тартым күші мәнін есептейді. және айналу жиілігі
және айналу жиілігі  ; I индексті және 2
; I индексті және 2 , (2.1 сурет).
, (2.1 сурет).