 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Основные числовые характеристики непрерывных сл. величин.
Мат. ожидание непр. сл. величины:
Дисперсия непрерывной случайной величины:
Среднее квадратическое отклонение непрерывной случайной величины: σ(X) = √D(X) Мода непрерывной случайной величины Mo(X) - значение с.в., имеющее наибольшую вероятность. Если в задаче требуется определить моду - находим экстремум (максимум) плотности вер-сти f(x). Асимметрия (коэффициент асимметрии) случайной величины As(X) - величина, характеризующая степень асимметрии распределения относительно математического ожидания.
Если коэффициент асимметрии отрицателен, то либо большая часть значений случайной величины, либо мода находятся левее математического ожидания, и наоборот, если As(X)>0, то правее. Эксцесс (коэффициент эксцесса) случайной величины Ex(X) - величина, характеризующая степень островершинности или плосковершинности распределения. Коэффициент эксцесса непрерывной случайной величины вычисляется по формуле:
Нормальный закон распределения (часто называемый законом Гаусса) на практике встречается чаще всего. В природе и различных областях человеческой деятельности весьма распространены случайные величины, которые представляют собой сумму большого числа независимых или слабо зависимых случайных величин. Распределения таких случайных величин большей частью бывают неизвестны и в то же время они хорошо аппроксимируются нормальным распределением. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.
Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т. д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному.
Нормальный закон распределения говорит о том, что случ. величина может принимать любые значения, и они появляются с различной частотой, но средние и близкие к ним встречаются наиболее часто. По мере удаления от среднего значения случ. величина встречается все реже (плотность распределения падает). График закона нормального распределения – имеет холмообразный вид, симметричен относительно прямой х = МХ.
Например, по нормальному распределению распределен рост людей, находящихся одновременно в большой аудитории. А именно: достаточно мало людей очень большого роста, и столь же мала вероятность встретить людей очень малого роста. В основном, легче встретить людей среднего роста — и вероятность этого велика. Нормальное распределение имеет плотность вероятности где a – мат.ожидание, σ - среднее квадратическое отклонение, т.е. σ2-дисперсия.
График нормального распределения имеет куполообразную форму, он симметричен относительно своего мат. ожидания, а на степень его островершинности влияет величина среднего квадратичного отклонения σ.
Асимметрия, эксцесс, мода и медиана нормального распределения равны: Поскольку интеграл от функции плотности вероятности
Геом.смысл ф-ции Лапласа – это площадь под куполообразной стандартной кривой нормального з-на распределения на промежутке [-х, х]. (как на предыд. рисунке)
Функция распределения сл.величины Х (распределенной по норм. з-ну) выражается через ф-ю Лапласа т.о.
Геом.смысл ф-ции распределения это площадь под куполообразной кривой нормального з-на распределения на промежутке (-∞, х).
Пример. Случайная величина Х имеет нормальное распределение с мат. ожиданием а=15 и средним квадр. отклонением σ=5. Найти вероятность того, что случайная величина Х примет значение, принадлежащее интервалу (10, 30).
Вероятность того, что нормально распределенная сл. величина Х примет значение, принадлежащее интервалу (α,β), равна: где а – мат. ожидание, σ – среднее квадратическое отклонение.
По условию α=15, β=30, а=15, σ=5. Следовательно,
«Правило трех сигм» Если случ.вел. Х имеет норм.з-н распр.с мат.ож. а и ср.-кв. отклон. σ2. то практически все ее значения заключены в промежутке (а - 3σ, а + 3σ).
Пример. Рост мужчин–величина нормально распределенная смат.ож. а=173 и ср-кв. отклон. σ2=36. Найти: 1)плотность вер-ти f(x) и ф-ю распред. F(x):
2) в выпуске доли костюмов роста 170-176 и 176-182: Р(170≤Х≤176) = Р(176≤Х≤182) = 3)правило трех сигм для сл. вел. Х: рост мужчин заключен в пределах (а - 3σ, а + 3σ), т.е. (173 - 3·6, 173 + 3·6) или (155, 191).
|



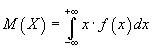



 ,
,
 , поскольку для нее составлены таблицы (Эти таблицы есть в учебниках в приложениях, в частности, в книге Крамера).
, поскольку для нее составлены таблицы (Эти таблицы есть в учебниках в приложениях, в частности, в книге Крамера). .
.

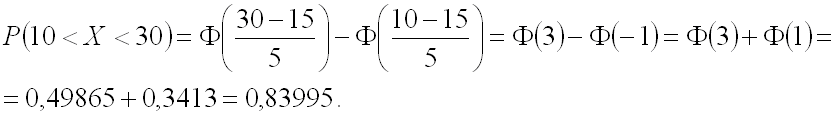


 .
. =
=  =
= 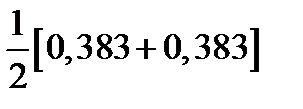 =0,383.
=0,383. =
=  =
=  =0,242.
=0,242.