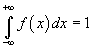 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Геометрическое распределение
Производится серия испытаний. Случайная величина - количество испытаний до появления первого успеха (например, бросание мяча в корзину до первого попадания). Закон распределения имеет вид:
Т.е. дискретная случ. величина Х имеет геом. распред. с параметром р и знаменателем q, если она принимает значения 1,2,3,… k, … с вероятностями Р(Х) = pqk-1, где q=1-р. Распределение называется геом., т.к. вер-ти р1, р2, … образуют геом.прогрессию, у которой первый член – р, а знаменатель – q. Если количество испытаний не ограничено, т.е. если случайная величина может принимать значения 1, 2, ..., ∞, то мат.ожидание и дисперсию геометр. распределения можно найти по формулам Mх = 1/p, Dх = q/p2 Пример. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель p = 0,6 при каждом выстреле. С.в. X - число возможных выстрелов до первого попадания. А) Составить ряд распределения, найти функцию распределения, построить её график и найти все числовые характеристики. б) Найти математическое ожидание и дисперсию для случая, если стрелок намеревается произвести не более трёх выстрелов.
а)Случайная величина может принимать значения 1, 2, 3, 4,..., ∞
Контроль: Σpi = 0,6/(1-0,4) = 1 (сумма геометрической прогрессии)
Ф-ция распределения - это вероятность того, что с.в. Х примет значение меньшее, чем конкретное числовое значение х. Значения функции распределения находим суммированием вероятностей. Если x ≤ 1, то F(x) = 0 Если 1 < x ≤ 2, то F(x) = 0,6 Mх = 1/p = 1/0,6 ≈ 1,667
б) Случайная величина может принимать значения 1, 2, 3.
Контроль: Σpi = 0,6 + 0,24 + 0,16 = 1 Если x ≤ 1, то F(x) = 0 Асимметрия и эксцесс Асимметрия – это свойство распределения выборки, которое характеризует несимметричность распределения случайной величины. На практике симметричные распределения встречаются редко и чтобы выявить и оценить степень асимметрии, вводят понятие асимметрии. В случае отрицательного коэффициента асимметрии более пологий «спуск» наблюдается слева, в противном случае – справа. В первом случае асимметрию называют левосторонней, а во втором – правосторонней.
Коэффициент асимметрии дискретной случайной величины вычисляется по формуле: σ3 Коэфф. асимметрии непрерывной сл.вел. вычисляется по формуле:
Эксцесс – это мера крутости кривой распределения. Коэффициент эксцесса дискретной случайной величины вычисляется по формуле: Ex(X) = [(x1- MX)4p1 + (x2- MX)4p2 + ... + (xn- MX)4pn] / σ4 - 3 Коэффициент эксцесса непрерывной случайной величины вычисляется по формуле:
Пример. Закон распределения дискретной случайной величины X – это перечень всех возможных значений сл.вел. X , которые она может принимать, и соответствующих вероятностей. Сумма всех вер-ей должна равняться 1. Проверка: 0,1 + 0,2 + 0,5 + 0,1 + 0,1 = 1.
Непрерывная случайная величина принимает не какие-либо конкретные числовые значения, а любые значения на числовом отрезке. Описание закона распределения в непрерывном случае существенно сложнее, чем в дискретном. Непрерывной называют случайную величину, которая может принимать любые значения из некоторого заданного интервала, например, время ожидания транспорта, температура воздуха в каком-либо месяце, отклонение фактического размера детали от номинального, и т.д. Интервал, на котором она задана, может быть бесконечным в одну или обе стороны.
Главное различие в задачах вычисления вероятностей для дискретного и непрерывного случаев состоит в следующем. В дискретном случае длясобытий типа х = с (случайная величина принимает определенное значение) ищется вероятность Р(с). В непрерывном случае вероятности такого типа равны нулю, поэтому интерес представляют вероятности событий типа «случайная величина принимает значения из некоторого отрезка», т.е. а ≤ х ≤ b. Или для событий типа х ≤ с ищется вероятность р(х ≤ с). Получили график функции распределения F(х ≤ с).
Итак, разнообразие случайных величин весьма велико. Число принимаемых ими значений может быть конечным, счетным или несчетным; значения могут быть расположены дискретно или заполнять интервалы сплошь. Для того чтобы задавать вероятности значений случайных величин, столь различных по своей природе, и притом задавать их одним и тем же способом, в теории вероятностей вводят понятие функции распределения случайной величины. Пусть
Резюмируем сказанное: случайной величиной называется величина, значения которой зависят от случая и для которой определена функция распределения вероятностей. Для непрерывных случайных величин (когда множество возможных значений случайной величины несчетно) закон распределения задается при помощи функции. Чаще всего это функция распределения: F(x) = P(X<х). Функция F(x) обладает следующими свойствами: 1. 0 ≤ F(x) ≤ 1 2. F(x) не убывает; 3. F(x) непрерывна слева; 4. F(-∞) = 0, F(∞) = 1.
С помощью функции распределения можно вычислять вероятности попадания случайной величины Х в различные промежутки вида х1<X<х2 P(х1<X<х2) = F(x2)- F(x1) Пример. Известно, что По определению Пример.Ф-я распред. сл.вел.Х имеет вид: Решение. P(1<X<3) = F(3)- F(1) = 1- ½= ½.
Производная от ф-ции распределения непр.сл.величины Х называется плотностью распределения вероятностей Х: f(x) = F/(x). Значит, ф-я распределения это интеграл:
Вер-ть попадания непр.случ.величины в [a; b]: Вер-ть попадания непр.случ.величины в (-∞; х]:
Для дискрет.сл.вел. мы находили мат. ожид., дисперсию, среднекв. отклонение. Их аналогами для непр.сл.вел. являются:
Пример.Случ.вел. Х задана плотностью распределения на отрезке [0; 1]: f(x) =1. Решение:
Плотность вероятности непрерывной случайной величины или функция распределения вероятностей - аналог закона распределения дискретной с.в. Но если закон распределения дискретной с.в. графически изображается в виде точек, соединённых для наглядности ломаной линией, то плотность вероятностей графически представляет собой непрерывную гладкую линию. Аналитически задаётся формулой.
Если закон распределения дискретной с.в. ставит каждому значению x в соответствие определённую вероятность, то про плотность распределения такого сказать нельзя. Для непрерывных с.в. можно найти только вероятность попадания в какой-либо интервал. Считается, что для каждого отдельного значения непрерывной с.в. вероятность равна нулю. Основное свойство плотности вероятности: несобственный интеграл от плотности вероятности в пределах от -∞ до +∞ равен единице (геометрически это выражается тем, что площадь фигуры, ограниченной сверху графиком плотности вероятности, снизу - осью OX, равна 1).
Функция распределения случайной величины - это функция, определяющая для каждого значения x вероятность того, что случайная величина (ξ) примет значение меньшее, чем x: F(x) = P(ξ < x). Численно функция распределения равна площади фигуры, ограниченной сверху графиком плотности вероятности, снизу осью ОХ, с боков - рассматриваемым интервалом. |
— случайная величина и х - произвольное действительное число. Вероятность того, что 
;
. Найти F(2).
. След, 
. 
.
. Найти вероятность того, что сл. вел. Х примет значение в промежутке [1, 3).
и 
.
