ПОЗНАВАТЕЛЬНОЕ

Сила воли ведет к действию, а позитивные действия формируют позитивное отношение

Как определить диапазон голоса - ваш вокал

Игровые автоматы с быстрым выводом

Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими

Целительная привычка

Как самому избавиться от обидчивости

Противоречивые взгляды на качества, присущие мужчинам

Тренинг уверенности в себе

Вкуснейший "Салат из свеклы с чесноком"

Натюрморт и его изобразительные возможности

Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.

Как научиться брать на себя ответственность

Зачем нужны границы в отношениях с детьми?

Световозвращающие элементы на детской одежде

Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия

Как слышать голос Бога

Классификация ожирения по ИМТ (ВОЗ)

Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Математическое ожидание дискретной случайной величины

Дискретные случайные величины

Для дискретной случайной величины закон распреде­ления может быть задан в виде таблицы, аналитически (в виде формулы) или графически.

Итак, пусть случайная величина Xможет принимать одно из п различных значений: х₁, х₂, … ,х_п.

При этом каждое из этих значений величина X принимает с опреде­ленной вероятностью — соответственно р₁, р₂, …, р_n.

Иначе, р₁— это вер. события "случайная величи­на Xприняла значение х₁илиХ=х₁",

р₂ — вер. случайного события X = х₂, и т.д…. р_п — вероятность случайного события X = х_п.

Сведем все эти значения в таблицу:

В первой строке - значения, принимаемые случайной величиной X, во второй строке — их вероятности. Она называется таблицей распределения случайной величины X. Обычно числа в первой строке таблицы распределения располагают в порядке воз­растания.

Замечание. Поскольку в результате испытания величина X наверняка примет одно из этих значений, то для таблицы распределения случайной величины спра­ведливо равенство р₁+ р₂ + …+ р_n = 1.

Итак, для того чтобы при решении конкретной задачи заполнить таблицу распределения заданной случайной величины, надо выпи­сать все принимаемые ею значения х₁, х₂, … , х_п и вычислить соот­ветствующие вероятности р₁, р₂, …, р_n.

Пример Будем кидать игральный кубик большое количество раз. Количество очков, которое выпадет на кубике при каждом броске, является случайной величиной и может принимать любые натуральные значения от 1 до 6. Для случайной величинывероятности принять любое из шести значений равны между собой. Таблица распределе­ния выглядит так:

Обратить внимание, что р₁+ р₂ + …+р₆ = 6 ·¹/₆ =1.

Пример с тремя монетами. В результате одновременного бросания трех монет возможно всего 8 равновероятных исходов: ГГГ, ГГР, ГРГ, ГРР, РГГ, РГР, РРГ, РРР.

При 1-м исходе величина Х (число гербов)принимает значение 3;

при 2-м, 3-м и 5-м — значение 2;

при 4-м, 6-м и 7-м — значение 1;

при 8-м — значение 0.

С учетом этого таблица распределения случайной величины Y:

Обратить внимание, что р₁+ р₂ + …+р₄ = 2 ·¹/₈ + 2 ·³/₈ =1.

Для более наглядного представления закона распределения ча­сто используется координатная плоскость. По оси Ох отмеча­ют значения, принимаемые случайной величиной, по оси Оу — вероятности. Затем на плоскости (х, р) отмечают точки и получают столбчатую диаграмму:

Математическое ожидание дискретной случайной величины

Будем кидать игральный кубик большое количество раз. Количество очков, которое выпадет на кубике при каждом броске, является случайной величиной и может принимать любые натуральные значения от 1 до 6. Среднее арифметическое выпавших очков, подсчитанных за все броски кубика, тоже является случайной величиной, однако при больших N оно стремится к вполне конкретному числу – математическому ожиданию Mx .

Мат. ожиданием или средним значением случайной величины называется число, обозначаемое Мх: это среднее ожидаемое значение, принимаемое случайной величиной в больших сериях испытаний.

Мат. ожидание дискретной случайной величины x, . Оно показывает, какое значение случайная величина примет в среднем при большом числе испытаний.

Мат. ожидание непрерывной случайной величины с плотностью вероятностей p(x) вычисляется с помощью интегралов и нами не рассматривается.

Пример. Будем кидать игральный кубик большое количество раз. Математическое ожидание Mх =3,5. Каким образом получилась эта величина? Пусть в N испытаниях n₁ раз выпало 1 очко, n₂ раз – 2 очка и так далее.

Тогда

При N → ∞, т.е. при очень большом количестве бросков, количество исходов, в которых выпало одно очко, или два, или три,… одинаково, т.е. .

Отсюда .

Пример. Лотерея. Разыгрываются две вещи стоимостью по 10 руб. и одна стоимостью 30 руб. Определить математическое ожидание чистого выигрыша для студента, если он приобрел 1 билет стоимостью 1 руб., а всего билетов 50.

Решение. Пусть Х - случайная величина, характеризующая сумму чистого выигрыша для студента.

Х может принять значение: -1, если студент ничего не выиграет;

9, если его выигрыш - 10 руб.;

29, если его выигрыш - 30 руб.

Чтобы определить математическое ожидание выигрыша, необходимо определить вероятность каждого выигрыша:

Закон распределения случайной величины Х имеет вид

X	-1
p

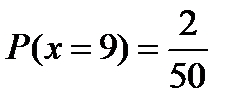
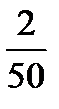
Причем, . Мат. ожидание .