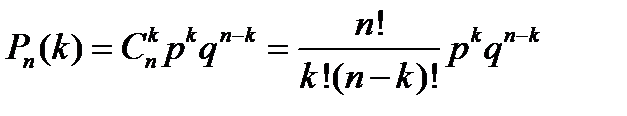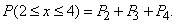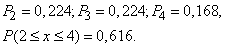ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Биномиальное распределение

1 234 5

Пусть производится п независимых испытаний, в каждом из которых некоторое событие А может появиться с вер-ю р. тогда вер-ть противоположного события (ненаступления А) равна q=1-р. Рассм. ситуацию, при котор. из п испытаний событие А произошло k раз и не произошло (п – k) раз. Вер-ть такого события дается формулой Бернулли:

Пример. Тест из 4 вопросов, на каждый из которых дано 4 ответа (только один - правильный). Найти вер-ть правильного ответа на 2, 3, и 4-й вопросы при ответе «наугад».

Решение. Вер-ть правильного ответа каждый раз р=0,25. Вер-ть неправильного ответа q=1-р=0,75.

Биномиальным называют закон распределения дискретной случайной величины X - числа появлений события в n независимых испытаниях, в каждом из которых вероятность наступления события постоянна. Вероятности p_i вычисляют по формуле Бернулли

Для биномиального распределения:

математическое ожидание Mх = np,
дисперсия Dх = npq,
мода np-q ≤ Mo ≤ np+p,
коэффициент асимметрии As = (q - p)/√npq,
коэффициент эксцесса Ex = (1 - 6pq)/npq

Пример. Построить закон распределения числа попаданий мячом в корзину при трех бросках, если вероятность попадания при одном броске равна 0,6. Найти среднее число попаданий и дисперсию.

Случайная величина Х – число попаданий в корзину при трёх бросках. Соответствующие вероятности найдём по формуле Бернулли.

Искомый закон распределения:

Мат. ожидание: М_Х = Σ х_ip_i = 0 · 0,064 + 1 · 0,288 + 2 · 0,432 + 3 · 0,216 = 1,8
Или: М_Х = np = 3 · 0,6 = 1,8
Дисперсия: D_Х = Σ х²_ip_i – (М_Х)² = 0² · 0,064 + 1² · 0,288 + 2² · 0,432 + 3² · 0,216 – 1,8² = 0,72
Или: D_Х = npq = 3 · 0,6 · 0,4 = 0,72
Сред.квадр. отклонение: σ = √Dх ≈ 0,85
Коэффициент асимметрии As = (q - p)/√npq = (0,4 - 0,6)/√3·0,6·0,4 ≈ -0,2357

Пример. Вычислить вероятность того, что событие, имеющее вероятность p = 0.5, в n = 10 испытаниях произойдет m = 1 раз.

C₁₀¹ = 10,

P₁ = 10 · 0.5¹ · (1 – 0.5)^{10 – 1} = 10 · 0.5¹⁰ = 0.0098.

Как видим, вер. наступления этого события достаточно мала. Объясняется это, во-первых, тем, что абсолютно не ясно, произойдет ли событие или нет, поскольку вероятность равна 0.5 и шансы здесь «50 на 50»; а во-вторых, требуется исчислить то, что событие произойдет именно один раз (не больше и не меньше) из десяти.

Пример. Вычислить вероятность того, что событие, имеющее вероятность p = 0.5, в n = 10 испытаниях произойдет m = 2 раза.

C₁₀² = 45,

P₂ = 45 · 0.5² · (1 – 0.5)^{10 – 2} = 45 · 0.5¹⁰ = 0.044. Вер-ть наступления этого события стала больше!

Пример. Увеличим вероятность наступления самого события. Вычислить вероятность того, что событие, имеющее вероятность p = 0.8, в n = 10 испытаниях произойдет m = 1 раз.

C₁₀¹ = 10,

P₁ = 10 · 0.8¹ · (1 – 0.8)^{10 – 1} = 10 · 0.8¹ · 0.2⁹ = 0.000004. Вероятность стала меньше, чем в первом примере! Ответ, на первый взгляд, кажется странным, но поскольку событие имеет достаточно большую вероятность, вряд ли оно произойдет только один раз. Более вероятно, что оно произойдет большее, чем один, количество раз. Действительно, подсчитывая P₀, P₁, P₂, P₃, …, P₁₀ (вероятность того, что событие в n = 10 испытаниях произойдет 0, 1, 2, 3, …, 10 раз), мы увидим:

C₁₀⁰ = 1, C₁₀¹ = 10, C₁₀² = 45, C₁₀³ = 120, C₁₀⁴ = 210, C₁₀⁵ = 252,
C₁₀⁶ = 210, C₁₀⁷ = 120, C₁₀⁸ = 45, C₁₀⁹ = 10, C₁₀¹⁰ = 1;

P₀ = 1 · 0.8⁰ · (1 – 0.8)^{10 – 0} = 1 · 1 · 0.2¹⁰ = 0.0000…;
P₁ = 10 · 0.8¹ · (1 – 0.8)^{10 – 1} = 10 · 0.8¹ · 0.2⁹ = 0.0000…;
P₂ = 45 · 0.8² · (1 – 0.8)^{10 – 2} = 45 · 0.8² · 0.2⁸ = 0.0000…;
P₃ = 120 · 0.8³ · (1 – 0.8)^{10 – 3} = 120 · 0.8³ · 0.2⁷ = 0.0008…;
P₄ = 210 · 0.8⁴ · (1 – 0.8)^{10 – 4} = 210 · 0.8⁴ · 0.2⁶ = 0.0055…;
P₅ = 252 · 0.8⁵ · (1 – 0.8)^{10 – 5} = 252 · 0.8⁵ · 0.2⁵ = 0.0264…;
P₆ = 210 · 0.8⁶ · (1 – 0.8)^{10 – 6} = 210 · 0.8⁶ · 0.2⁴ = 0.0881…;
P₇ = 120 · 0.8⁷ · (1 – 0.8)^{10 – 7} = 120 · 0.8⁷ · 0.2³ = 0.2013…;
P₈ = 45 · 0.8⁸ · (1 – 0.8)^{10 – 8} = 45 · 0.8⁸ · 0.2² = 0.3020… (самая большая вероятность!);
P₉ = 10 · 0.8⁹ · (1 – 0.8)^{10 – 9} = 10 · 0.8⁹ · 0.2¹ = 0.2684…;
P₁₀ = 1 · 0.8¹⁰ · (1 – 0.8)^{10 – 10} = 1 · 0.8¹⁰ · 0.2⁰ = 0.1074…

Разумеется, P₀ + P₁ + P₂ + P₃ + P₄ + P₅ + P₆ + P₇ + P₈ + P₉ + P₁₀ = 1.

Распределение Пуассона

Пусть имеется некоторая последовательность событий, наступающих в случайные моменты времени (будем называть это потоком событий). Интенсивность потока (среднее число событий, появляющихся в единицу времени) равна λ. Пусть этот поток событий - простейший (пуассоновский), т.е. обладает тремя свойствами:

1) вероятность появления k событий за определённый промежуток времени зависит только от длины этого промежутка, но не от точки отсчёта, другими словами, интенсивность потока есть постоянная величина (свойство стационарности);

2) вероятность появления k событий в любом промежутке времени не зависит от того, появлялись события в прошлом или нет (свойство «отсутствия последействия»);

3) появление более одного события за малый промежуток времени практически невозможно (свойство ординарности).

Вер. того, что за промежуток времени t событие произойдёт k раз, равна

Мат.ожидание и дисперсия случ.величины, распределенной по з-ну Пуассона равны М_х=D_x=λt

Распределение Пуассона имеют: поток входящих телефонных звонков на коммутатор, поломки оборудования, длительность исполнения ремонтных работ стабильно работающим сотрудником, ошибка печати, рост колонии бактерий, дефекты в длинной ленте, проводе или цепи.

Пример. Среднее число вызовов, поступающих на АТС за 1 мин, равно двум. Найти вероятность того, что за 4 мин. поступит: а) три вызова; б)менее трёх вызовов; в)не менее трёх вызовов. Поток вызовов - простейший.

Используем формулу Пуассона. λ = 2, t = 4.
P(0) = 8⁰·e^-8/0! = e^-8 ≈ 0,000335
P(1) = 8¹·e^-8/1! = 8e^-8 ≈ 0,002684
P(2) = 8²·e^-8/2! = 32e^-8 ≈ 0,010735
P(3) = 8³·e^-8/3! = 85,33e^-8 ≈ 0,014313
а) P(k=3) = 0,014313
б) P(k<3) = P(0) + P(1) + P(2) = 0,013754
в) P(k≥3) = 1 - P(k<3) = 1 - 0,013754 = 0,986246

Пример. На ткацком станке нить обрывается в среднем 0,375 раза в течение часа работы станка. Найти вероятность того, что за смену (8 часов) число обрывов нити будет заключено в границах 2 и 4 (не менее 2 и не более 4 обрывов).

λ = 0,375, t = 8. λt =0,375·8 = 3.

Пример. В ящике находится n = 100 деталей, как качественных, так и бракованных. Вероятность достать бракованное изделие составляет p = 0.01. Мы вынимаем изделие, определяем, бракованное оно или нет, и кладем его обратно. Какова вероятность, что из 100 изделий, которые мы перебрали, два оказались бракованными?

По распр. Пуассона:

Пример. По некоторой цели производится 50 независимых выстрелов. Вероятность попадания в цель при одном выстреле равна 0,04. Найти приближенно вероятность того, что в цель попадет: ни одного снаряда, один снаряд, два снаряда.

1 234 5