 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Дисперсия дискретной случайной величины
Математическое ожидание не может в достаточной степени характеризовать случайную величину. Например, при одинаковой средней величине осадков, выпадающих в двух местностях за год, нельзя сказать, что климат этих местностей одинаков. Например, пусть случайные величины X и Y заданы следующими законами распределения, представленными в таблицах.
Математические ожидания их одинаковы и равны нулю: Mх = –0.1·0.1–0.01·0.2+0·0.4+0.01·0.2+0.1·0.1 = 0; Mу = –20·0.3–10·0.1+0·0.2+10·0.1+20·0.3 = 0. Однако характер распределения их различный: Случайная величина Х может принимать значения, мало отличающиеся от математического ожидания (см. в таблице: для х значения близки к мат. ожиданию, т.е. к нулю). Случайная величина Y может принимать значения, значительно отклоняющиеся от математического ожидания (см. в таблице: для у значения сильно отличаются от мат. ожидания, т.е. от нуля). Иными словами, по математическому ожиданию нельзя судить о том, какие отклонения от него возможны. А тем не менее умение дать оценку рассеяния имеет важное значение. Самой используемой характеристикой разброса значений случайной величины является дисперсия. Дисперсия случайной величины характеризует меру разброса случайной величины около ее мат. ожидания или степень отклонения случайной величины от её среднего значения. Дисперсия случайной величины это число Dх = М(х-Мх)2 = М(х)2 - (Мх)2. Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны. Пример. Вычислить дисперсии для случайных величин X и Y, законы распределения которых приведены в предыдущей таблице. Решение Dх = (–0.1–0)2·0.1 + (–0.01–0)2·0.2 + (0–0)2·0.4 + (0.01–0)2·0.2+(0.1–0)2·0.1 =0.00204; Dу = (–20–0)2·0.3 + (–10–0)2·0.1 + (0–0)2·0.2 + (10–0)2·0.1 + (20–0)2·0.3 = 260. Таким образом, при одинаковых математических ожиданиях дисперсия величины Х очень мала (0.00204), а случайной величины Y значительная (260). В общем случае, если дисперсия случайной величины мала, то малы отклонения от мат. ожидания, а если существуют значения xi, сильно отклоняющиеся от мат. ожидания, то они маловероятны. Если же дисперсия велика, то это указывает на существование значений случайной величины, которые сильно отклоняются от её математического ожидания, причем не все они маловероятны. Пример. Найти дисперсию случайной величины Х, которая задана следующим законом распределения:
Решение. Найдем математическое ожидание: Mх= 1·0.3+2·0.5+5·0.2 = 2.3 Найдем Mх2= 12·0.3+22·0.5+52·0.2 = 7.3 Найдем Dх= 7.3 - 2.32 = 2.01 Пример. Найти дисперсию случайной величины Х, имеющей следующий закон распределения:
Решение:Mх= 1·0.1+2·0.2+3·0.3+4·0.3+5·0.1 = 3.1 Mх2= 12·0.1+22·0.2+32·0.3+42·0.3+52·0.1 = 10.9 Dх= 10.9 - 3.12 = 1.29 Пример. Найти дисперсию случайной величины Х, которая задана следующим законом распределения:
Среднеквадратическим отклонением дискретной случайной величины x называется корень квадратный из дисперсии этой величины:
Пример. Игральный кубик кидают большое количество раз. Дисперсия: Среднеквадратическое отклонение
Итак. Законом распределенияслучайной величины называется любое правило (таблица, функция), позволяющее находить вероятности всех возможных событий, связанных со случайной величиной. Вспомним, что случайная величина называется дискретной, если множество ее возможных значений конечно или счетно. Для дискретных случайных величинзакон распределения с конечным множеством значений задается при помощи таблицы.
(с помощью таблицы мы можем найти числовые х-ки дискрет. сл. величины: мат. ожид., дисперсию, среднекв. отклонение) Кроме мат. ожид., дисперсии и среднекв.отклонения используют другие числовые характеристики, отражающие особенности распределения. Идея этих х-к очень проста: вместо того чтобы рассматривать все значения переменной, а их может быть очень много (тысячи и миллионы), вначале стоит просмотреть описательные х-ки. Они дают общее представление о значениях, которые принимает переменная. Мода и медиана. Квантили. Модой Мо дискретной случайной величины называется ее наиболее вероятное значение, (модой Монепрерывной случайной величины – значение, в котором плотность вероятности максимальна.) показать на рис.2 Мода представляет собой наиболее часто встречающееся значение переменной (иными словами, наиболее «модное» значение переменной), например, популярная передача на телевидении, модный цвет платья или марка автомобиля и т. д. Пример.Если ряд распределения дискретной случайной величины Х имеет вид: то Мо = 2.
Медиана Ме случ. величины Х это такое ее значение, при котором Р(Х<Ме) =Р(Х>Ме)=½ Т.е. вер. того, что сл.вел. примет значение меньшее или большее медианы Ме одна и та же, равная ½.
Медиана разбивает всю выборку на две равные части. Половина значений переменной лежит ниже медианы, половина — выше. Медиана дает общее представление о том, где сосредоточены значения переменной, иными словами, где находится ее центр. В некоторых случаях, например, при описании доходов населения, медиана более удобна, чем среднее. При решении практических задач часто требуется найти значение x, при котором функция распределения F(x) случайной величины Х принимает заданное значение q, т.е. требуется решить уравнение F(xq) = Р(Х<xq) = q. Решения такого уравнения (соответствующие значения x) в теории вероятностей называются квантилями. Квантили представляют собой значения, которые делят две половины выборки (разбитые медианой) еще раз пополам. Таким образом, медиана и квартили делят диапазон значений переменной на четыре равные части. Для некоторых q уравнение F(xq) = q может иметь несколько решений, для некоторых - ни одного. Это означает, что для соответствующей случайной величины некоторые квантили определены неоднозначно, а некоторые квантили не существуют.
Различают верхнюю квартиль, которая больше медианы и делит пополам верхнюю часть выборки (значения переменной больше медианы), и нижнюю квартиль, которая меньше медианы и делит пополам нижнюю часть выборки. Нижнюю квартиль часто обозначают символом 25%, это означает, что 25% значений переменной меньше нижней квартили. Верхнюю квартиль часто обозначают символом 75%, это означает, что 75% значений переменной меньше верхней квартили.
Квантили, наиболее часто встречающиеся в практических задачах, имеют свои названия: медиана - квантиль уровня0.5; нижняя квартиль - квантиль уровня0.25; верхняя квартиль - квантиль уровня0.75; децили - квантили уровней0.1, 0.2, …, 0.9; процентили - квантили уровней 0.01, 0.02, …, 0.99. С понятием квантиля тесно связано понятие процентной точки. Под 100q% -ой точкой понимается квантиль х1-q. Т.е. такое значение сл.вел. Х, при котором Р(Х> х1-q) = q. Пример.Случ.вел. Х задана плотностью распределения на отрезке [0; 1]: f(x) =3х2. Найти моду, медиану, мат.ожид., квантиль х0,3 и 30% точку сл.вел. Х. 1. плотность вер-ти максимальна при х=1, след. мода Мо=1. 2. Медиану Ме=b найдем из условия: 3. Мат.ожидание 4. Функция распределения Из уравнения F(xq) = q найдем квантиль х0,3: (х0,3)3 = 0,3, х0,3= 5. Найдем 30% точку сл.вел. Х или квантиль х0,7 из уравнения (х0,7)3 = 0,7. х0,7= |





 . Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего.
. Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего.

 (площадь фигуры под кривой распределения делится пополам)
(площадь фигуры под кривой распределения делится пополам) решаем:
решаем:  . Отсюда находим b:
. Отсюда находим b:  . Ме=b
. Ме=b .
. .
. .
. .
.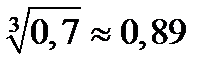 .
.