 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Электрический колебательный контур. Собственные колебания. Формула Томсона
Для наглядности воспользуемся методом аналогии и проанализируем по одной схеме механические и электрические колебания. Рассмотрим колебания груза массой m на пружине (рис. 21.1).
Рис. 21.1.
В таблице 21.1 представлены значения кинематических и энергетических величин, характеризующих процесс колебания груза массой m на пружине в различные моменты времени. Таблица 21.1.Процесс гармонического колебания
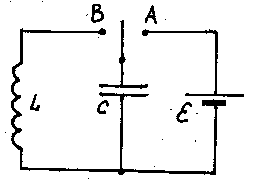
Рассмотрим электрические колебания в колебательном контуре. Колебательным контуром называется цепь, составленная из катушки индуктивности и конденсатора. Будем считать, что катушка индуктивности обладает только реактивным индуктивным сопротивлением. Такая катушка называется идеальной (рис. 21.2).
Рис. 21.2. Для вывода системы из состояния равновесия надо сообщить ей энергию. Если ключ перевести в положение А, то конденсатор будет заряжаться:
Если после этого ключ перевести в положение В, то в контуре возникнут гармонические колебания:
Коэффициент
где w0 – частота собственных колебаний контура. Между током и напряжением будет сдвиг фаз на половину периода. Таким образом, в электрической цепи возникают незатухающие колебания, которые характеризуются периодическими изменениями во времени величины тока, заряда и напряжения на обкладках конденсатора, а также взаимными превращениями энергии электрического поля конденсатора и энергии магнитного поля катушки индуктивности. В таблице 21.2 представлены значения электрических и энергетических величин, характеризующих процесс свободных незатухающих электрических колебаний в идеальном колебательном контуре в различные моменты времени.
Таблица 21.2.Электрические колебания в идеальном контуре.
Опыт 21.1.Электрические колебания в колебательном контуре Цель работы: Изучить электрические колебания в колебательном контуре Оборудование: 1. Конденсатор переменной емкости (от 0 до 60) 2. Катушка индуктивности 3. Осциллограф
Рис.21.3 Ход работы. Установка состоит из конденсатора переменной емкости от 0 до 60,5 мкФ и катушки индуктивности, в качестве которой служит дроссельная катушка с замкнутым железным сердечником от разборного трансформатора. В качестве индикатора электрических колебаний в контуре используется школьный демонстрационный осциллограф. С Помощью переключателя конденсатор подключается либо к источнику постоянного тока, либо к катушке индуктивности. 1. Введем максимальную емкость 60,5мкФ и максимальную индуктивность. Сердечник замкнут ярмом. Заряжаем конденсатор и переключаем его на катушку индуктивности. Луч осциллографа совершает затухающие колебания. При этом пятно на экране осциллографа перемещается медленно. 2. Уменьшим емкость конденсатора до 20мкФ и повторим опыт. Луч осциллографа колеблется с большей частотой. Можно уменьшить емкость конденсатора до 3-4мкФ. Частота колебания луча значительно возрастет. Таким образом, качественно подтверждается зависимость частоты или периода электрических колебаний в контуре от электроемкости конденсатора. Чем больше емкость конденсатора, тем меньше частота или больше период электрических колебаний в контуре. 3. Восстановим максимальную емкость конденсатора. Разомкнем сердечник. Индуктивность катушки уменьшилась. Зарядим конденсатор и замкнем его на катушку индуктивности. Частота электрический колебаний в контуре увеличится, период уменьшится. Вывод: Выполнив опыты, мы убедились, что при замыкании заряженного конденсатора на катушку индуктивности в контуре возникают электрические колебания. |




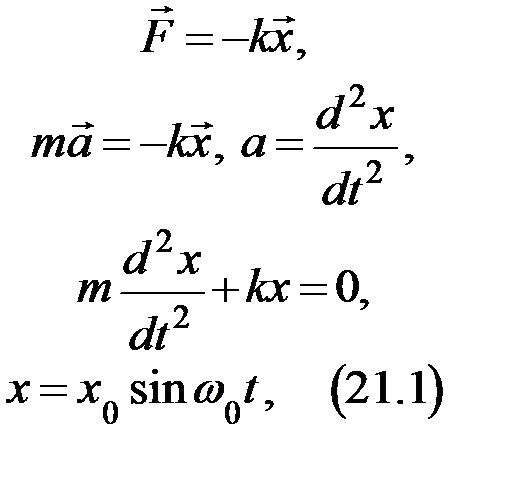
 – частота собственных колебаний.
– частота собственных колебаний.




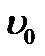




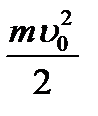
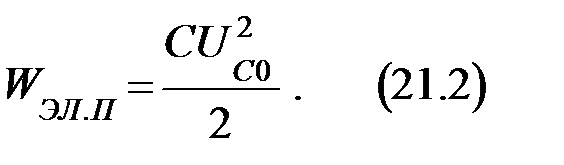

 можно обозначить как
можно обозначить как 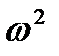 :
: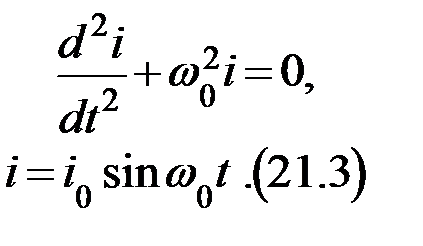










 в цепи пойдет ток за счет запасенной энергии. Запас энергии будет уменьшаться, и ток будет слабеть.
в цепи пойдет ток за счет запасенной энергии. Запас энергии будет уменьшаться, и ток будет слабеть. заряд на обкладках сменится на противоположный.
заряд на обкладках сменится на противоположный. по отношению к первоначальному току ток будет иметь противоположное направление.
по отношению к первоначальному току ток будет иметь противоположное направление. через период восстановится исходная картина.
через период восстановится исходная картина.