 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Закон Био - Савара - Лапласа. Магнитное поле прямого, кругового и соленоидального токов.
Значение магнитной индукции для любого проводника определяется законом Био - Савара - Лапласа.
Рис. 15.8.
Вектор Вывод формулы напряжённости магнитного поля прямого тока (рис. 15.9; рис. 15.10) . Применим формулу
Рис. 15.9.
Подставим эти значения в формулу магнитной индукции:
Угол
Таким образом, магнитная индукция поля прямого тока определяется формулой: Для того, чтобы получить напряженность магнитного поля, необходимо разделить правую часть формулы (15.8) на
Рис. 15.10
Вывод формулы напряжённости магнитного поля кругового тока (рис. 15.11). Рассмотрим поле, создаваемое током, текущим по тонкому проводу, имеющему форму окружности (круговой ток). Определим магнитную индукцию кругового тока
Рис. 15.11 Рассмотрим индукции Закон Био - Савара - Лапласа для двух элементов:
Выбрав dl1=dl2 и принимая, что r1=r2, получим:
Проинтегрируем это выражение по всему контуру и заменим r на
В частности, при x=0 имеем:
магнитная индукция в центре кругового тока Напряженность магнитного поля в центре кругового тока равна:
Формула для расчета напряженности магнитного поля кругового тока на его оси принимает вид:
Вывод формулы напряжённости магнитного поля соленоидального тока. Соленоид представляет собой тонкий провод, навитый плотно, виток к витку, на цилиндрический каркас. В отношении создаваемого им поля соленоид эквивалентен системе одинаковых круговых токов с общей прямой осью. Бесконечно длинный соленоид симметричен относительно любой перпендикулярной к его оси плоскости. Взятые попарно симметричные относительно такой плоскости витки создают поле, магнитная индукция которого перпендикулярна к плоскости. Следовательно, в любой точке внутри и вне соленоида вектор
Рис. 15.12.
Возьмем прямоугольный контур 1-2-3-4. Циркуляцию вектора
Из четырех интегралов, стоящих в правой части, второй и четвертый равны нулю, так как вектор Взяв участок 3-4 на большом расстоянии от соленоида(где поле заведомо должно быть очень слабым), третьим слагаемым можно пренебречь. Следовательно, можно утверждать, что :
Здесь В - магнитная индукция поля в тех точках, где располагается отрезок 1-2, Если отрезок 1-2 проходит внутри соленоида на любом расстоянии от его оси, контур охватывает суммарный ток
Откуда: а напряженность магнитного поля соленоидального тока равна:
Отметим, что полученный нами результат не зависит от того, на каком расстоянии от оси (но внутри соленоида) располагается отрезок 1-2. Если этот отрезок располагается вне соленоида, то охватываемый контуром ток равен нулю, вследствие чего:
Откуда В=0. Таким образом, вне бесконечного длинного соленоида магнитная индукция равна нулю, внутри - всюду одинакова и имеет величину, определяемую формулой (15.14). По этой причине в учении о магнетизме бесконечно длинный соленоид играет такую же роль, как плоский конденсатор в учении об электричестве. В обоих случаях поле однородно и полностью заключено внутри конденсатора (электрическое) и внутри соленоида(магнитное). Произведение Тесты к лекции №15 Тест 15.1.Магнитная индукция поля, создаваемого отрезком бесконечно тонкого прямолинейного проводника, вычисляется по формуле…
£ £ £ £
Тест 15.2.Магнитная индукция в центре кругового тока определяется по формуле… £ £ £ £
Тест 15.3.Форма существования материи, обладающая свойством передавать магнитное взаимодействие. £ магнитное поле £ магнитная индукция £ пробный контур £ магнитный момент Тест 15.4.Дайте определение пробного контура. £ контур, вносящий помехи в исходное поле. £ контур, усиливающий исходное поле. £ контур, ослабляющий исходное поле. £ контур, который не создает заметных искажений исходного поля.
Тест 15.5.Формула £ вектор магнитной индукции £ напряженность магнитного поля £ магнитную индукцию £ магнитный момент Вихревой характер магнитного поля. Циркуляция вектора индукции магнитного поля. Магнитный поток. Сила Ампера. Работа по перемещению проводника с током в магнитном поле. Сила Лоренца. Определение удельного заряда электрона[11] 16.1. Вихревой характер магнитного поля. Циркуляция вектора индукции магнитного поля. Магнитный поток 16.2. Сила Ампера 16.3. Работа по перемещению проводника с током в магнитном поле 16.4. Сила Лоренца 16.5. Определение удельного заряда электрона
|
-в векторной форме, (15.6)
- в скалярной форме. (15.7)
всегда перпендикулярен плоскости, построенной на векторах 
и 
. С помощью закона Био - Савара - Лапласа рассчитаем магнитную индукцию поля прямого, кругового и соленоидального токов.
для вычисления полей простейших токов. Рассмотрим поле, создаваемое током, текущим по бесконечному прямому проводу (Рис. 15.9) .Все dBв данной точке имеют одинаковое направление. Поэтому сложение векторов dBможно заменить сложением их модулей. Точка, для которой мы вычисляем магнитную индукцию, находится на расстоянии b от провода. Из рисунка 15.9 видно, что:
.
для всех элементов бесконечно прямого тока изменяется в пределах от 0 до 
. Следовательно:
.
. (15.8 )
:
, создаваемых двумя элементами контура dl1 и dl2. Т. к. угол между r и dl равен 90°, то sin 90°=1.
получим:
(15.10)
(15.11)
(15.12)
(15.13)
может иметь лишь направление, параллельное оси.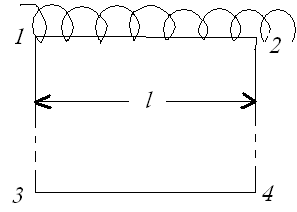
-длина этого отрезка.
, где 
- число витков соленоида, приходящееся на единицу его длинны, 
- сила тока в соленоиде. Поэтому согласно :
(15.14)
(15.15)
.
называется числом ампер - витков на метр.
выражает: