 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Работа по перемещению проводника с током в магнитном поле.
Введя понятие потока магнитной индукции, можно рассчитать работу по перемещению проводника с током в магнитном поле (рис 16.6). Пусть проводник CD под действием силы Ампера может перемещаться из начального положения в конечное положение C1D1. Тогда работа по его перемещению будет равна:
где DS=l×x – т.н. “покрытая” площадь, DF=ВDS – изменение магнитного потока.
Рис. 16.7. Сила Лоренца Рассчитаем силу, которая действует на один отдельно взятый движущийся заряд q (рис. 16.7)
Рис. 16.8.
Осуществим подстановки:
где Сила Лоренца, действующая на один отдельно взятый движущийся заряд:
или, в векторной форме:
Если движется положительный заряд (q>0), то Если движется отрицательный заряд (q<0), то Рассмотрим частные случаи движения заряженной частицы в магнитном поле. 1.
Рис. 16.9. Уравнение движения x=vt. 2.
Отсюда
Траектория движения – окружность.
Рис. 16.10. Период вращения по определению:
Подставив (16.15) в (16.16), получим :
3. Частица влетает под произвольным углом Выбираем систему координат и разложим вектор скорости на две составляющие. Применим принцип независимости движений Галилея:
OY: равномерное движение по окружности в плоскости, перпендикулярной силовым линиям.
Период обращения:
Траектория – винтовая линия. Параметры: радиус винта и шаг. Шаг винта – расстояние, которое проходит заряд вдоль оси винта за время Т.
Рис. 16.11.
Измерив экспериментально параметры траектории, можно определить величину удельного заряда частицы Опыт 16.2.Сила Лоренца. Цель работы: Изучить силу Лоренца Оборудование: 1. Осциллографическая трубка 2. Эбонитовая палочка, мех 3. Постоянный магнит
Рис. 16.12. Ход работы. 1. Пучок заряженных частиц электронов в осциллографической трубке изменяет направление движения при поднесении как отрицательно заряженной эбонитовой палки, так и постоянного магнита. Обратите внимание, что изменение полярности конца подносимого магнита приводит к изменению направления смещения электронного пучка на противоположное. Вывод: Сила Лоренца зависит от индукции магнитного поля.
16.5.Определение удельного заряда электрона Метод магнитной фокусировки Буш применил для определения удельного заряда электрона метод магнитной фокусировки. Суть этого метода заключается в следующем. Допустим, что в однородном магнитном поле вылетает из некоторой точки слегка расходящийся пучок электронов, имеющих одинаковую по величине скорость υ, Направления, по которым вылетают электроны, образуют с направлением В небольшие углы a. Электроны в этом случае движутся по спиральным траекториям, совершая за одинаковое время (16.18) полный оборот и смещаясь вдоль направления поля на расстояние (16.20). Вследствие малости углов a расстояния (16.20) для данных электронов оказываются практически одинаковыми и равными υT (для малых углов cosa»1). Следовательно, слегка расходящийся пучок сфокусируется в точке, отстоящей от точки вылета электронов на расстояние:
В опыте Буша электроны, испущенные раскаленным катодом К (рис. 16.11), ускоряются, проходя разность потенциалов U, приложенную между катодом и анодом А. В результате они приобретают скорость υ, значение которой может быть найдено из соотношения:
Рис. 16.13 [3]. Вылетев затем из отверстия в аноде, электроны образуют узкий пучок, направленный вдоль оси эвакуированной трубки, вставленной внутрь соленоида. На входе в соленоид помещается конденсатор, на который подается переменное напряжение. Поле, создаваемое конденсатором, отклоняет электроны пучка от оси прибора на небольшие изменяющиеся со временем углы a. Это приводит к “завихрению” пучка – электроны начинают двигаться по различным спиральным траекториям. На выходе из соленоида ставится флуоресцирующий экран. Если подобрать магнитную индукцию В так, чтобы расстояние h¢ от конденсатора до экрана удовлетворяло условию: h¢=nh (16.23) (h – шаг спирали, n – целое число), то точка пересечения траекторий электронов попадет на экран – электронный пучок окажется сфокусированным в этой точке и возбудит на экране резкое светящееся пятно. Если условие не соблюдается, светящееся пятно на экране будет размытым. Решив совместно уравнения (16.21),(16.22) и (16.23), можно найти e/m и υ. Наиболее точное значение удельного заряда электрона, установленное с учетом результатов, полученных разными методами, равно
Тесты к лекции №16 Тест 16.1.Отметьте формулу работы по перемещению проводника с током в магнитном поле: £ £ £ £
Тест 16.2.Формула силы Лоренца в векторной форме: £ £ £ £
Тест 16.3.Модуль силы Лоренца определяется по формуле… £ £ £ £
Тест 16.4.От чего зависит направление силы Лоренца и вызываемое отклонение заряженной частицы в магнитном поле? £ среды, в которой происходит взаимодействие £ знака заряда q £ от скорости частицы £ нет правильных вариантов ответа Тест 16.5.Какова траектория заряженной частицы, движущейся под произвольным острым углом к вектору магнитной индукции поля? £ винтовая линия, ось которая совпадает с линией индукции магнитного поля. £ окружность, плоскость которой перпендикулярна индукции магнитного поля. £ прямая, параллельная линии индукции магнитного поля. £ прямая, перпендикулярная линии индукции магнитного поля.
Магнетики. Намагниченность. Связь индукции и напряженности магнитного поля в магнетике. Магнитная проницаемость и восприимчивость. Магнитомеханические явления[11] 17.1. Магнетики. Намагниченность. Связь индукции и напряженности магнитного поля в магнетике. Магнитная проницаемость и восприимчивость 17.2. Магнитомеханические явления При рассмотрении магнитного поля в вакууме, естественно, не учитывался характер взаимодействия магнитного поля с веществом (ввиду отсутствия последнего). Если же в магнитное поле, создаваемое свободными движущимися зарядами, попадает кусок вещества, возникает взаимодействие поля свободных зарядов с молекулами данного вещества. Для описания этого взаимодействия каждой молекуле вещества стали приписывать некоторый магнитный момент, а реакция совокупности молекул вещества на внешнее магнитное поле характеризуется вектором намагниченности:
Рис. 17.1 [3]. Вектор намагниченности – физическая величина, численно равная суммарному магнитному моменту всех молекул, заключенных в единице объема. Под действием внешнего магнитного поля, магнитные моменты молекул вещества будут в той или иной степени изменятся и поворачиваться, подобно тому, как ориентируется виток с током во внешнем магнитном поле. Тогда по принципу суперпозиции результирующее поле в веществе будет складываться из внешнего магнитного поля
где
Эксперименты свидетельствуют о том, что для большинства веществ намагниченность
где
где |
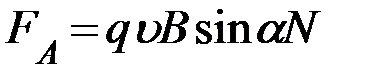, (16.11)
.
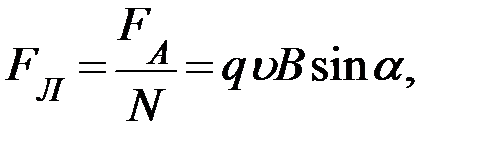(16.12)
(16.13)
.
.
Движение прямолинейное и равномерное, т.е. 
, где 
.
.(16.15)
.
,
,
. (16.18)
. (16.19)
.
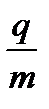(16.21)
(16.22)
, созданного свободными движущимися зарядами или токами вне вещества, и собственного (наведенного) магнитного поля 
, возникающего как реакция вещества на внешнее магнитное поле:
, (17.2)
- индукция магнитного поля в вакууме.
, (17.3)
- магнитная проницаемость вещества.
– магнитная восприимчивость вещества.