 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Двухмассовая колебательная система
Следует отметить, что любую вибрационную строительно-дорожную машину в первом приближении можно представить в виде двухмассовой колебательной системы с двумя степенями свободы. Мi – колеблющиеся массы, ki – коэффициенты упругого сопротивления, bi – коэффициент вязкого трения. Результаты анализа динамических моделей машин представили в виде таблицы, где «плюс» означает наличие данного элемента модели, «минус» - его отсутствие
Уравнение движения масс такой системы известно и представляется в виде
Общим решением этой системы является сумма общего решения системы однородных уравнений и частного решения системы. В общее решение будет входить слагаемое, соответствующее свободным колебаниям с собственной частотой системы, и слагаемое, описывающее только вынужденные колебания масс системы с частотой вынуждающей силы. Собственные колебания системы зависят от начальных условий и с течением времени быстро затухают, поэтому рассматривается решение только для установившихся вынужденных колебаний. Учитывается также, что во всех машинах, согласно приведенной таблице всегда присутствует только одна вынуждающая сила. В случае глубинного вибратора Р1=Р2, b2=0, k2=0 и система распадается на 2 независимые одномассовые колебательные системы. Частное решение уравнений движения системы следует искать в виде x1=a1cosj1coswt+a1sinj1sinwt x2=a2cosj2coswt+a2sinj2sinwt ai – амплитуда колебаний масс ji – углы сдвига фаз перемещений относительно вынуждающей силы. Если взять первые и вторые производные от x1 и x2 по времени и принять сначала wt=0, то для двух угловых частот колебаний получится система восьми алгебраических уравнений. В результате анализа можно сделать вывод о следующем виде АЧХ и ФЧХ для двухмассовой колебательной системы.
М – масса вибросистемы b – коэффициент сопротивления
k, r – коэффициенты линейной и нелинейной упругости F(t) – периодическая вынуждающая сила
Распространение колебаний Колеблющееся материальное тело, помещенное в упругую среду, будет увлекать за собой и приводить в колебательное движение прилегающее к нему частицы среды. Последние в свою очередь, будут воздействовать на соседние частицы и приводить их также в колебательное движение и т.д. При этом существенно, что увлекаемые частицы среды будут несколько отставать по фазе от ранее приходивших в движение частиц, т.к. передача колебания от точки к точке всегда осуществляется с конечной скоростью, характерной для данной среды. Таким образом, колеблющееся материальное тело, помещенное в упругую среду, становится источником колебаний, распространяющихся от него во все стороны. Этот процесс распространения колебаний в упругой среде называется волной. Камень, брошенный в воду, вызывает распространение от места падения однократно не периодической поверхностной волны. Тело, гармонически колеблющееся на поверхности воды, вызывает распространяющиеся, периодически повторяющиеся поверхностные волны. Волна, проходящая через данную точку среды, характеризуется определенным направлением распространения. Область пространства, внутри которой колеблются все частицы среды, называется волновым полем. Граница, отделяющая колеблющиеся частицы от частиц, еще не начавших колебаться, носит название фронта волны. В однородной среде направление распространения перпендикулярно к фронту волны. Частица среды, до которой дошел фронт волны, приходит в колебательное движение, амплитуда, частота и направление которого в пространстве зависят от амплитуды, частоты и направлении колебаний предшествующих частиц. Направление движения колеблющихся точек может не совпадать с направлением распространения волны. На рисунке изображена длинная проволочная спираль, витки которой упруго связаны друг с другом. Возбудим колебания крайнего витка в точке 0. Волна начнет Скорость движения каждой колеблющейся точки непрерывно меняется по величине и зависит, как мы установили выше, от амплитуды, частоты и фазы колебаний. В противоположность этому скорость перемещения фронта данной волны в однородной среде постоянна. Она зависит только от свойств среды и характера колебания. Для выяснения основных характеристик распространяющейся волны, напишем уровнение называемое уравнением луча.
x – расстояние от 0 до М u - скорость волны в рассматриваемой упругой среде. Точки в которых смещение y достигает своего максимального значения ymax=+А называют гребнями волны, а точки в которых y принимает минимальное значение ymin= -А, – впадинами. Расстояние между двумя соседними гребнями или впадинами носит название длинны волны. Скорость волны равна ее частоте (т.е. число волн, испускаемых источником в секунду), умноженной на длину волны. За время Т волна перемещается на расстояние l. u=l/Т=nl Подставляя это выражение получаем уравнение луча в следующем виде
|





 Существуют другие динамические модели вибрационных машин. Их движение описывается другими уравнениями. Например
Существуют другие динамические модели вибрационных машин. Их движение описывается другими уравнениями. Например
 - сила трения
- сила трения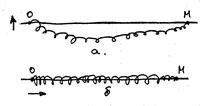 распространяться вдоль спирали по направлению ОМ. На рисунке (а) изображен случай, когда мы заставляем крайний виток колебаться в направлении перпендикулярном к ОМ. В этом случае и для всех последующих витков направление колебаний будет перпендикулярным к направлению их распространения. Подобные волны называют поперечными. На рисунке (б) изображен иной случай, когда направление колебаний параллельно направлению распространения. Подобные волны называют продольными.
распространяться вдоль спирали по направлению ОМ. На рисунке (а) изображен случай, когда мы заставляем крайний виток колебаться в направлении перпендикулярном к ОМ. В этом случае и для всех последующих витков направление колебаний будет перпендикулярным к направлению их распространения. Подобные волны называют поперечными. На рисунке (б) изображен иной случай, когда направление колебаний параллельно направлению распространения. Подобные волны называют продольными.
 - промежуток времени на который отстает начало колебаний произвольной точки М от начальной точки.
- промежуток времени на который отстает начало колебаний произвольной точки М от начальной точки.