 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Упругие и квазиупругие силы
Выясним какими силами вызываются гармонические колебания, воспользовавшись законами динамики. По второму закону динамики сила F, действующая на материальную точку численно равна произведению массы точки m на ее ускорение w. Подставляя в это соотношение найденное ранее выражение w для гармонического колебания, определим значение силы
Рассмотрим движение материальной точки массы m под действием упругой пружины массой которой пренебрежем. Точка движется вдоль вертикальной оси x так, что сила тяжести не оказывает влияния на ее движение. Точка 0 на оси x отвечает положению равновесия материальной точки, т.е. положению при котором пружина не деформирована. При смещении точки вверх на величину x на нее будет действовать сила F упругости растянутой пружины равная закону Гука: Fупр=-kx<0. Эта сила направлена вниз т.е. к положению равновесия точки 0. При смещении материальной точки вниз от 0 на величину x на нее будет действовать сила Fупр=-kx>0 направленная вверх, т.к. x<0. Следовательно, при любых смещениях от положения, равновесия т.е. от точки 0, материальная точка будет находиться под действием силы, направленной к 0 и равной Fупр=-kx. Сравнивая F=-kx и Fупр=-kx видим, что материальная точка m, будучи выведена из состояния равновесия, начнет совершать гармонические колебания. Коэффициент k есть коэффициент упругости, или жесткости пружины. Численно он равен силе, которую нужно приложить к пружине, чтобы растянуть (или сжать) пружину на единицу длины. Частоту колебаний материальной точки М под действием пружины (массой которой мы пренебрегаем) с коэффициентом упругости k можно получить из mw2=k Эта частота колебаний называется частотой собственных колебаний системы и обозначается w0, это частота колебаний системы за счет внутренних сил.
Частота и период не зависят от амплитуды колебаний и определяются только величинами m и k. Амплитуда и фаза колебаний (или начальная фаза j0) определяются из начальных условий, при которых возникло движение. Аналогичное гармоническое движение возникает и при движении груза m, подвешенного на пружине с учетом действия ускорения свободного падения. Отличие от рассмотренного выше случая состоит в том, что положение равновесия будет иметь место при несколько растянутой пружине. Упругая сила растяжения в положении равновесия в точности ровна силе тяжести и будет направлена вверх. Уравновешивает ее: Чтобы материальная точка m совершала гармонические колебания не обязательно, чтобы на нее действовали именно упругие силы. Достаточно, чтобы сила при смещении от положения равновесия менялось согласно закону F=-kx. Если сила, не являющаяся по своей природе упругой, подчиняется закону F=-mw2x=-kx, то она называется «квазиупругой» силой (по латыни «quasi» означает «как-бы»). Рассмотрим пример гармонического колебательного движения под действием квазиупругих сил.
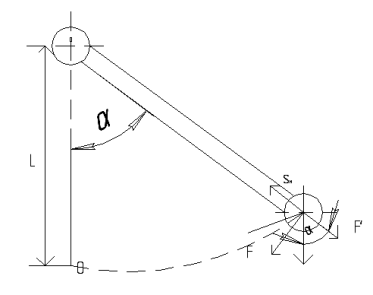
Математический маятник Маятник настенных часов представляет собой настенный груз, который укреплен на длинном тонком стержне, подвешенном шарнирно на горизонтальной оси C перпендикулярно стержню. В первом приближении пренебрежем массой стержня и будем считать всю массу груза m сосредоточенной в его центре М. Подобная система, состоящая из материальной точки m, подвешенная на невесомом твердом стержне или нерастяжимой нити длинны СМ=L, называется математическим маятником.
Отклоним стержень на некоторый угол a от вертикали и разложим мысленно силу веса P=mg, действующую на точку М на 2 составляющие F¢ и F, направленные соответственно вдоль стержня и перпендикулярно к нему. Сила F¢=Pcosa будет растягивать стержень и уравновесится реакцией стержня S. Неуравновешенной останется составляющая силы F=Psina. Таким образом на точку М будет действовать 2 силы P и S, направленные под углом p-a друг к другу. Равнодействующая этих сил по правилу параллелограмма будет сила F=Psina, направленная по касательной к дуге ОМ в сторону точки 0. Когда груз придет в наинизшее положение, т.е. в точку 0, силы P и S полностью уравновесится. Таким образом точка 0 есть положение равновесия груза m. Обозначим отрезок дуги ОМ, характеризующий путь, пройденный точкой М из положения равновесия, через x и будем считать угол a и величину x положительными при отклонении стержня с грузом вправо от вертикали и отрицательными – при отклонении влево. Угол a измеряемый в радианах численно равен отношению длинны дуги x, на которую он опирается к радиусу окружности l, тогда (с учетом направления) сила F, действующая на точку М, может быть выражена в виде
Для малых углов отклонения от вертикали не превышающих 5-6°, т.е. при a<0,1 с достаточной степенью точности можно заменить sina углом a (в радианах). Тогда сила, действующая на точку М будет равна Сравнивая это выражение с F=-kx видим, что результирующая сила F, действующая на математический маятник, находящийся в поле земного тяготения, является квазиупругой силой с коэффициентом k=mg/l.Поэтому математический маятник будет совершать гармоническое колебательное движение с периодом
Амплитуда колебаний А и начальная фаза колебаний j0 будут зависеть от начального смещения и начальной скорости точки М. Реальный, так называемый физический маятник при малых углах отклонения от вертикали будет также совершать гармонические колебания. Из соотношения Поэтому передвижением груза относительно маятника можно регулировать ход часов с маятником. Если часы отстают, то надо передвигать груз ближе к оси и наоборот. Лекция 3 |
действующей на точку в каждый момент времени. Сравнивая это уравнение с 
замечаем, что 
, где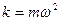 
, т.е. сила, вызывающая гармонические колебания, обладает двумя важными свойствами:
Кроме того из F=-kx следует, что при x=0 и F=0, т.е. в центре колебания 0 на точку М сила не действует. Иными словами, центр колебаний является положением равновесия точки М.
тогда период 
.
следует, что период колебаний математического маятника не зависит от его массы m, а определяется лишь его длинной l и ускорением силы тяжести g в данной точке земного шара. Период колебаний физического маятника зависит также не от массы маятника m, а от распределения масс в нем и характеризуется отношением I/m, где I – момент инерции системы относительно центра колебаний, а m – масса всей системы. В последнем случае можно ввести понятие приведенной длины физического маятника 
, тогда период колебаний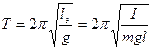 
.