 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Энергия гармонических колебаний.
При гармоническом колебательном движении кинетическая энергия колеблющейся материальной точки непрерывно меняется. Меняется и потенциальная энергия взаимодействия между точкой и окружающими телами, приводящего к появления квазиупругих сил. Мы не буде интересоваться природой возникновения сил взаимодействия, главное, что она квазиупруга и нам известен коэффициент k. Как сила, так и потенциальная энергия при этом определяются положением колеблющейся точки М, т.е. ее координатой x. Полная энергия механического движения есть сумма кинетической и потенциальной энергий. Согласно
Пользуясь известным тригонометрическим выражением Уравнение для Екин принимает выражение
Таким образом Екин меняется со временем также по гармоническому закону, но по сравнению с координатой x с удвоенной частотой. Кроме того значение Екин колеблется не около 0, а около
При вычислении потенциальной энергии квазиупругих сил условимся отсчитывать ее от положения равновесия, т.е. при x=0 и Епот=0. Тогда потенциальная энергии в точке x будет численно равна работе квазиупругой силы, совершенной при перемещении из положения равновесия в данную точку взятую с обратным знаком
Подставляя вместо x его значение получаем
Следовательно, потенциальная энергия Епот меняется частотой 2w и в тех пределах, что и Екин, но со сдвигом фазы на p. Найдем теперь полную энергию Е материальной точки M, совершающей гармонические колебания с частотой w и амплитудой А
Таким образом, полная энергия гармонически колеблющейся точки есть величина постоянная и пропорциональна квадрату амплитуды А2. В процессе движения происходит переход кинетической энергии в потенциальную и обратно, но сумма их остается постоянной. Когда точка проходит через положение равновесия x=0, то потенциальная энергия обращается в нуль, а кинетическая максимальной и равна полной. Когда же точка доходит до одного из своих крайних положений x=±А, то u=0, то кинетическая энергия обращается в ноль, потенциальная максимальна и равна полной. Затухающие колебания В условиях, когда на тело действует только одна квазиупругая сила, оно будет совершать незатухающие гармонические колебания с постоянной амплитудой А=const. На реально же движущиеся тела всегда будут действовать со стороны окружающей среды силы трения, препятствующие их движению. На преодоление сопротивления среды, на трение в опорах, на создание волн, на возникновение не упругих деформаций и т.п. будет затрачиваться энергия. Вследствие этого механическая энергия колеблющегося тела будет непрерывно уменьшаться переходя в другие формы энергии и рассеиваясь в окружающую среду. Согласно с тем что
Полная сила F, действующая на колеблющуюся точку будет тогда суммой квазиупругой силы Fкв.упр и силы трения Fтр. При малых скоростях движения сопротивление обычно пропорционально первой степени скорости и направлено противоположно ей т.е. Fтр=-bu, где b – коэффициент трения, зависящий от свойств среды, формы и размеров движущегося тела. Чтобы решить задачу о колебательном движении при наличии трения, вернемся к уже разработанной задаче о гармоническом колебательном движении и найдем строгое математическое ее решение. Заменяя во втором законе динамики ускорение w второй производной от смещения по времени, получим основное дифференциальное уравнение одномерного движения При наличии только одной квазиупругой силы равной –kx это уравнение принимает вид Mx¢¢=-kx Это и есть дифференциальное уравнение движения материальной точки массы М под действием квазиупрогой силы с коэффициентом жесткости k. Неизвестная функция x(t) в этом выражении встречается в чистом виде и виде второй производной. Для решения этого уравнения вспомним, что функциями которые при двукратном дифференцировании превращаются сами в себя являются sin и cos. Поэтому решать будем в виде x=Acos(wt+j0) c с произвольными значениями постоянных А, j0, w. Введение j0 необходимо для объединения sin и cos в одну функцию. Выполняя двукратное дифференцирование этого выражения по t и подставив x и x¢¢ в диф. Уравнение движения получаем
Если сократить на Аcos(wt+j0), то получаем Mw2=k или Таким образом мы математически подтвердили правильность уравнения частоты собственных колебаний системы. Разберем аналогичным образом затухающие колебания при наличии сил трения F=Fк.у.+Fтр=-kx-bu=-kx-bx получаем диф. уравнение движения Mx¢¢=-bx’-kx’ Mx¢¢+bx’+kx=0 Это диф. уравнение движения системы под действием квазиупругих сил и сил трения. Решение такого диф. уравнения ищется в виде
Решение довольно трудоемкое. Можно отметить, что в результате получается система из двух уравнений Решив эти уравнения находим что
Это частота собственных колебаний системы на которую действуют силы трения.
Отличительной особенностью амплитуды является то, что если раньше она была постоянной, то теперь изменяется по экспоненциальному закону А(t)=A0e-at который является затухающей функцией. Амплитуда затухающих колебаний за каждый период убывает в одно и то же количество раз. И скорость этого затухания определяется логарифмическим декрементом затухания Вынужденные колебания (одномассовая колебательная система)
Для получения не затухающих колебаний необходимо воздействие дополнительной переменной внешней силы, которая подталкивала бы точку то в одну, то в другую сторону и работа которой непрерывно восполняла бы убыль энергии, затрачиваемой на преодоление трения. Подобная переменная сила называется вынуждающей Fвын, а возникшие под ее действием не затухающие колебания называются вынужденными. Разберем простейший случай вынуждающей силы, меняющейся по закону синуса или косинуса Fвын=F0coswt, где F0 – амплитуда вынуждающей силы, т.е. ее максимальное значение. Полная сила действующая на колеблющуюся точку будет алгебраической суммой квазиупругой силы, силы трения и вынуждающей силы. Диф. уравнение движения примет вид Mx¢¢=-kx-bx¢+F0coswt Mx²+bx+kx=F0coswt Как известно из курса высшей систематики, решение этого уравнения x(t)=xсвоб(t)+xвын(t) представляет собой сумму свободных колебаний и вынуждающих колебаний. Свободные колебания будут происходить с собственной угловой частотой Поэтому пренебрегая собственными колебаниями системы, будем искать решение уравнения в виде: x=xвын(t)=Acos(wt+j), с неизвестными заранее амплитудой А и сдвигом фазы j - между силой и направлением движения . Решив данное диф. уравнение получаем
1. w<w0 j»0 Точка следует за направлением силы. В измерительной технике, для регистрации быстропеременных усилий 2. w>w0 j»p Движение точки противоположно направлению действия сил. Устойчивый режим работы всех виброприборов. 3. w=w0 Резонанс – резкое увеличение амплитуды колебаний системы при совпадении частот вынуждающей и собственной. Отрицательные и положительные проявления. Усиление слабых колебаний. Лекция 4 |
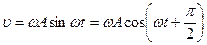
меняясь от 0 до 
. Удвоение частоты Екин объясняется тем, что за один период скорость точки дважды обращается в ноль.
с уменьшением энергии колебаний будет уменьшаться его амплитуда и колебания станут затухающими.
.
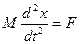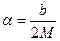
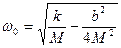
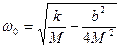и довольно быстро затухнут. Таким образом частота вынужденных колебаний должна совпадать с частотой колебаний вынуждающей силы. Амплитуда этих колебаний должна быть постоянной, т.к. постоянна амплитуда вынуждающей силы.
