 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Уравнения односторонних реакций 0-го, 1-го и 2-ого порядка
Рассмотрим зависимость концентрации реагирующих веществ С от времени t для необратимых (односторонних) реакций нулевого, первого и второго порядков. Для получения зависимости С от t для реакций всех порядков надо проинтегрировать соответствующее дифференциальное уравнение (2.1.5-2.1.10) при начальном условии: С = С0 при t = 0.
Реакции нулевого порядка
Подставим в уравнение (2.1.5) выражение (2.1.2), с учетом того, что расчет ведется по исходному веществу А (что обусловливает выбор знака «минус»):
После разделения переменных и интегрирования в пределах времени от 0 до t и концентраций – от С0 до С получаем:
или
Отсюда видно, что концентрация реагирующего вещества линейно убывает со временем. Размерность константы скорости равна размерности скорости реакции. Подставляя в это выражение C = C0/2, найдем время, за которое прореагирует половина исходного вещества,t1/2 (время полупревращения):
Реакции первого порядка
Подставим в уравнение (2.1.6) выражение (2.1.2):
Интегрирование дает:
Видно, что константа скорости первого порядка имеет размерность, обратную времени (с-1). Подставляя C = C0/2, найдем время полупревращения:
T.е., время полупревращения для реакций первого порядка не зависит от исходной концентрации реагирующего вещества. Из уравнения (2.1.13) следует линейная зависимость логарифма концентрации от времени. Отсюда можно определить константу скорости, используя экспериментальные данные.
Рис. 2.1.3. Зависимость логарифма концентрации от времени для реакций первого порядка.
Т.о., логарифм концентрации для реакции первого порядка линейно зависит от времени (рис. 2.1.3, уравнение (2.1.13)) и константа скорости численно равна тангенсу угла наклона прямой к оси времени:
Реакции второго порядка
Рассмотрим простейший случай, когда кинетическое уравнение имеет вид (2.1.7). В этом случае с учетом (2.1.2) можно записать:
После разделения переменных и интегрирования при граничных условиях времени от 0 до t и концентраций – от С0 до С получаем:
или
Подставляя C = C0/2, найдем время полупревращения:
Таким образом, время полупревращения для реакций второго порядка обратно пропорционально исходной концентрации реагирующего вещества С0. Для реакций второго порядка, характерна линейная зависимость обратной концентрации от времени (рис. 2.1.4) и константа скорости равна тангенсу угла наклона прямой к оси времени:
Рис. 2.1.4. Зависимость обратной концентрации от времени для реакций второго порядка
Порядок химической реакции есть формальное понятие; физический смысл порядка реакции для элементарных (одностадийных) реакций заключается в следующем: порядок реакции равен числу одновременно изменяющихся концентраций. В случае элементарных реакций, как уже отмечалось ранее, порядок реакции равен сумме коэффициентов в стехиометрическом уравнении реакции; однако в общем случае порядок реакции определяется только из экспериментальных данных и зависит от условий проведения реакции. Рассмотрим в качестве примера элементарную реакцию гидролиза этилового эфира уксусной кислоты (этилацетата):
СН3СООС2Н5 + Н2О ––> СН3СООН + С2Н5ОН
Если проводить эту реакцию при близких концентрациях этилацетата и воды, то общий порядок реакции равен двум и кинетическое уравнение имеет следующий вид:
При проведении этой же реакции в условиях большого избытка одного из реагентов (воды или этилацетата) концентрация вещества, находящегося в избытке, практически не изменяется и может быть включена в константу скорости; кинетическое уравнение для двух возможных случаев принимает следующий вид: 1) Избыток воды:
здесь
2) Избыток этилацетата:
В этих случаях мы имеем дело с реакцией псевдопервого порядка. Проведение реакции при большом избытке одного из исходных веществ используется для определения частных порядков реакции.
|




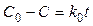
 (2.1.11)
(2.1.11) (2.1.12)
(2.1.12)
 (2.1.13)
(2.1.13) (2.1.14)
(2.1.14)



 (2.1.15)
(2.1.15) (2.1.16)
(2.1.16)





