 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Докажем, что, если остаток от деления числа на 9 есть 2, 3, 5, 6, 8, то это число не может быть квадратом целого числа.
Решение: Рассмотрим классы чисел, на которые разбивается множество целых чисел при делении на 9. 9k±1 (9k±1) 9k±2 (9k±2) 9k±3 (9k±3) 9k±4 (9k±4) 9k (9k) При делении на 9 целые числа, являющиеся полными квадратами дают в остатке числа 0, 1, 4, 7. Следовательно, числа, дающие в остатке 2, 3, 5, 6, 8 не могут являться квадратами целых чисел.
Делимость При решении задач на делимость следует знать основную теорему арифметики:натуральное число раскладывается на произведение простых множителей единственным образом, с точностью до порядка множителей, а так же признаки делимости. Признак делимости на 2. Число n делится на 2 в том и только в том случае, если его последняя цифра делится на 2. Признак делимости на 4.Число n делится на 4 в том и только в том случае, если на 4 делится число, образованное из двух последних цифр числа n. Признак делимости на 8.Число n делится на 8 в том и только в том случае, если на 8 делится трёхзначное число, образованное из трёх последних цифр числа n. Если внимательно рассмотреть признаки делимости на 2,4,8, то можно найти признак делимости на 2m(m=1,2,3,…): число n делится на 2m в том и только в том случае, если на 2m делится m-значное число, которое образуют m последних цифр числа n. Признак делимости на 5.Число n делится на 5 в том и только в том случае, если его последняя цифра 0 или 5. Признак делимости на 5m схож с признаком делимости числа n на 2m. Признак делимости на 3. Число n делится на 3 в том и только в том случае, если сумма его цифр делится на 3. Признак делимости на 9. Число n делится на 9 в том и только в том случае, если сумма его цифр делится на 9. Признак делимости на 7.Число n делится на 7 в том и только в том случае, если на 7 делится число p=n Признак делимости на 11.Число n делится на 11 в том и только в том случае, если сумма его цифр, стоящих на нечётных местах, отличается от суммы его цифр, стоящих на чётных местах, на величину кратную 11. (n Признак делимости на 13.Число n делится на 13 в том и только в том случае, если на 13 делится число l, полученное из n зачёркиванием последней цифры и прибавлением к получённому числу учетверённое значения зачеркнутой цифры. Комбинируя уже известные признаки делимости, можно узнать, делится ли данное число на 6, 10, 12, 14, 15 и так далее.
Пример1. Докажите, что произведение любых трех последовательных чисел делится на 6. Решение. Среди трех последовательных чисел есть как минимум одно четное и одно, делящееся на 3. Значит, их произведение разделится на 6.
Пример 2. Каково наименьшее натуральное N такое, что N! делится на 770? Решение. 770=7·11·10, значит N! делится на 11. Наименьшее выражение, содержащее множитель 11, будет 11!, в это произведение будут входить и 7, и 10.
Принцип Дирихле Разговор об олимпиадных задачах мы начинали с решения занимательных задач. Для учащихся 5-6 классов очень важен этот «занимательный» подход. Начнем с рассмотрения забавного перевода С. Я. Маршака одного шутливого английского стихотворения: Их было десять чудаков, Тех путников усталых, Что в дверь решили постучать Таверны «Славный малый». — Пусти, хозяин, ночевать, Не будешь ты в убытке, Нам только ночку переспать, Промокли мы до нитки. Хозяин тем гостям был рад, Да вот беда некстати: Лишь девять комнат у него, И девять лишь кроватей. — Восьми гостям я предложу Постели честь по чести, А двум придется ночь проспать В одной кровати вместе. Лишь он сказал, и сразу крик, От гнева красны лица: Никто из всех десятерых Не хочет потесниться. Как охладить страстей тех пыл, Умерить те волненья? Но старый плут хозяин был И разрешил сомненья. Двух первых путников пока, Чтоб не судили строго, Просил пройти он в номер «А» И подождать немного. Спал третий в «Б», четвертый в «В», В «Г» спал всю ночь наш пятый, В «Д», «Е», «Ж», «3» нашли ночлег С шестого по девятый. Потом, вернувшись снова в «А», Где ждали его двое, Он ключ от «И» вручить был рад Десятому герою. Хоть много лет прошло с тех пор, Неясно никому, Как смог хозяин разместить Гостей по одному. Иль арифметика стара, Иль чудо перед нами, Понять, что, как и почему, Вы постарайтесь сами. Внимательный читатель сразу заметит, что первого и второго путников в тексте сначала поместили в комнату «А», а потом одного из них невольно перебросили в десятую комнату, одного и того же человека подсчитали два раза. Гораздо проще задача может быть пояснена при помощи принципа Дирихле (Дирихле Петер Лежен (1805-1859) - немецкий математик, иностранный член многих иностранных академий наук). Представим этот принцип в такой шутливой форме: «Если в N клетках сидят не менее N+ I кроликов, то в какой-то из клеток сидит не менее двух кроликов». Обратим внимание на расплывчатость выводов - «в какой-то из клеток», «не менее». Это является, пожалуй, отличительной чертой принципа Дирихле, которая иногда приводит к возможности неожиданных выводов на основе, казалось бы, совершенно недостаточных сведений. Доказательство самого принципа чрезвычайно просто, в нем используется тривиальный подсчет кроликов в клетках. Если бы в каждой клетке сидело не более одного кролика, то всего в наших N клетках сидело бы не более N кроликов, что противоречило бы условиям. Таким образом, мы доказали принцип Дирихле методом «от противного». Задача 1. В мешке лежат шарики двух цветов: черного и белого. Какое наименьшее число шариков нужно достать из мешка вслепую, чтобы среди них заведомо оказались два шарика одного цвета? Решение. Достаем из мешка 3 шарика. Если среди этих шариков было не более одного шарика каждого из цветов - это очевидно, и противоречит тому, что мы достали три шарика. С другой стороны, понятно, что двух шариков может и не хватить. Ясно, что кроликами в этой задаче являются шарики, а клетками — цвета: черный и белый. Задача 2. Доказать, что среди п + 1 целого числа можно выбрать два, разность которых делится на п. Решение. При делении на п любое число дает в остатке одно из чисел 0, 1,2, 3, ..., п, т. е. существует всего п различных остатков. Поэтому среди п +1 числа найдутся два, дающие одинаковые остатки при делении на п. Разность этих чисел делится на п. Обобщенный принцип Дирихле Если в N клетках сидят не менее kN + 1 кроликов, то в какой-то из клеток сидит по крайней мере к + 1 кролик. Задача 3. В магазин привезли 25 ящиков с тремя разными сортами яблок (в каждом ящике яблоки только одного сорта). Доказать, что среди них есть по крайней мере 9 ящиков с яблоками одного и того же сорта. Решение. 25 ящиков-«кроликов» рассадим по трем клеткам-сортам. Так как 25 = 3 х 8 + 1, то применим «обобщенный принцип Дирихле» для N= 3, к = 8 и получим, что в какой-то клетке-сорте не менее 9 ящиков. Задача 4. Дано 8 различных натуральных чисел, каждое из которых не больше 15. Докажите, что среди их положительных попарных разностей есть три одинаковых. Решение. При решении этой задачи встречается, казалось бы, непреодолимое препятствие. Различных разностей может быть 14 — от 1 до 14 — это те же 14 клеток, в которые мы будем сажать кроликов. Кто же будет нашими кроликами? Ими, конечно, должны быть разности между парами данных нам натуральных чисел. Однако имеется 28 пар и их можно рассадить по 14 клеткам так, что в каждой клетке будет сидеть ровно два «кролика» (и значит, в каждом меньше трех). Здесь необходимо использовать дополнительное соображение: в клетке с номером 14 может сидеть не более одного кролика, ведь число 14 может быть записано только как разность двух натуральных чисел, не превосходящих 15, лишь одним способом: 14 = 15 — 1. Значит, в оставшихся 13 клетках сидят не менее 27 «кроликов» и применение обобщенного принципа Дирихле дает нам желаемый результат. Примечание. Заметим, что у нас в основе принципа Дирихле лежала идея сложения неравенств. Следствие. Если сумма п чисел равна S, то среди них есть как число, не большее S/ п, так и число, не меньшее S / п . Графы Определение. Под графом мы будем понимать картинку, адекватно описывающую задачу. При этом элементы множеств, как правило, показываются точками. Желательно, чтобы при решении точки не лежали на одной или паре прямых. Точки при этом называются вершинами графа, а линии, соединяющие эти точки, — ребрами. Отметим, что точки могут соединяться произвольными (не обязательно прямыми) линиями. Поясним понятие графа на примере нескольких задач. Пример 1. Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля — Меркурий, Плутон — Венера, Земля — Плутон, Плутон - Меркурий, Меркурий - Венера, Уран - Нептун, Нептун - Сатурн, Сатурн — Юпитер, Юпитер — Марс и Марс — Уран. Можно ли добраться (возможны пересадки) с Земли до Марса? Решение. Нарисуем схему: планетам будут соответствовать точки, а соединяющим их маршрутам - непересекающиеся между собой линии. Сделав набросок рисунка маршрутов, мы нарисовали граф, соответствующий условию задачи. Видно, что все планеты Солнечной системы разделились на две не связанных между собой группы. Земля принадлежит одной группе, а Марс - второй. Долететь с Земли до Марса нельзя.
Пример 2. В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией тогда и только тогда, когда двузначное число, составленное из цифр-названий этих городов, делится на 3. Можно ли из города 1 добраться в город 9? Решение. Покажем возможные маршруты, нарисовав граф
И в этой задаче 1 и 9 попали в две разных части графа. Ясно, что в правой части графа сгруппировались города-цифры нацело делящиеся на 3, а в левой части графа ребра соединяют две цифры: одну — делящуюся на 3 с остатком 1, а другую — делящуюся на 3 с остатком 2. Примечание. Отметим, что один и тот же граф можно нарисовать по-разному. Если учащиеся одного класса нарисуют графы к одной задаче, то мы можем получить столько графов, сколько учащихся их рисовали. Нарисованные по-разному графы (если они нарисованы без ошибок) принято называть изоморфными. Любой читатель может нарисовать бесконечное множество изоморфных графов.
Правило. Для подсчета числа ребер графа необходимо просуммировать степени вершин и полученный результат разделить на два. Следствие. Сумма степеней всех вершин графа должна быть четной (иначе ее нельзя было бы разделить на 2 нацело). Определение. Вершина графа, имеющая нечетную степень называется нечетной, а имеющая четную степень — четной. Теорема. Число нечетных вершин любого графа — четно. Для доказательства этой теоремы остается заметить, что сумма нескольких целых чисел четна тогда и только тогда, когда количество нечетных слагаемых четно. Примечание. Теорема о четности числа нечетных вершин - одно из центральных мест теории графов.
|



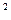 =81 k
=81 k 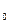 +3n
+3n  +2n
+2n 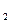 -(n
-(n  +3n
+3n 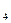 +n
+n 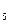 )+…,где n
)+…,где n 
