 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Какие остатки могут получиться при делении квадрата целого числа на 3?
Общие приемы решения Олимпиадных задач
Содержание
1. Инварианты и их применение при решении задач (четность, деление с остатком). 2. Делимость. 3. Принцип Дирихле и его применение при решении задач 4. Графы 5. Метод математической индукции 6. Игры ( игры шутки, симметрия, выигрышные позиции) 7. Олимпиадные задачи по геометрии
1.Инварианты и их применение при решении задач Инвариантом некоторого преобразования называется величина или свойство, не изменяющееся при этом преобразовании. В качестве инварианта чаще всего рассматриваются четность и остаток от деления. Причем, применение четности - одна из наиболее часто встречающихся идей при решении олимпиадных задач. Четность. Сформулируем свойства четности: 1. Сумма четных чисел четна 2. Сумма 2-х нечетных чисел четна. 3. Сумма четного и нечетного чисел нечетна. 4. Произведение любого числа на четное – четно. 5. Если произведение нечетно, то все сомножители нечетны. 6. Сумма четного количества нечетных чисел четна. 7. Сумма нечетного количества нечетных чисел нечетна. 8. Разность и сумма двух данных чисел – числа одной четности. 9. Если объекты можно разбить на пары, то их количество четно.
Лемма1. Четность суммы нескольких целых чисел совпадает с четностью количества нечетных слагаемых. Примеры: 1.Число 1+2+…+10- нечетное, так как в сумме 5 нечетных слагаемых. 2.Число 3+5+7+9+11+13- четное, так как в сумме 6 нечетных слагаемых. Лемма2. Знак произведения нескольких ( отличных от нуля) чисел определяется четностью количества отрицательных сомножителей. Примеры: 1. Число (-1)·(-2)·(-3)·(-4) положительно, так как в произведении четное число отрицательных сомножителей. 2. Число (-1) ·2·(-3)·4·(-5) отрицательно, так как в произведении нечетное число отрицательных сомножителей.
Пример1 Могут ли десять игрушек ценой в 3, 5 или 7 рублей стоить в сумме 53 рубля? Решение. Сумма четного количества нечетных чисел четна. У нас есть 10 игрушек, цена каждой игрушки - нечетное число, значит, их сумма должна быть четна. Но 53-число нечетное. Поэтому получить его в виде суммы 10 нечетных чисел нельзя. Пример2 Можно ли 7 телефонов соединить между собой попарно так, чтобы каждый был соединен ровно с тремя другими. Решение. При решении этой задачи используется такое соображение: если мы рассматриваем объекты типа веревки – провода, дороги, рукопожатия, знакомства и т.д., то при любом количестве объектов число концов должно быть четным. Предположим, что мы соединили 7 телефонов между собой попарно так, чтобы каждый был соединен ровно с тремя другими. Посчитаем количество концов проводов, соединяющих эти телефоны. Понятно, что их число должно быть четным. От каждого из 7 телефонов отходит 3 конца, всего 7·3=21 конец, число нечетное. Значит, нельзя 7 телефонов соединить между собой попарно так, чтобы каждый был соединен ровно с тремя другими. Пример3 Команд играют однокруговой турнир. Докажите, что в любой момент есть команда, сыгравшая четное число матчей. (однокруговой турнир – когда каждая команда играет с каждой ровно один раз). Указание. В общей сумме всех игр каждая игра учитывается два раза, если же подсчитать сумму игр 13 команд, сыгравших по нечетному числу матчей, результат будет нечетный. Чтобы общая сумма игр получилась четной, хотя бы одна команда должна сыграть четное число матчей.
Деление с остатком. Определение. Разделить целое число a на целое число b с остатком – это значит представить его в виде a=bq + r, где q и r целые числа, 0£r<ïbï. Основную роль во всей арифметике целых чисел играет теорема о делении с остатком. Теорема. Для любых целых a и b существует единственная пара чисел q и r, удовлетворяющих условиям, a=bq + r, 0£r<ïbï. Замечание. В частности, если Замечание. Если Из теоремы о делении с остатком следует, что при фиксированном целом m>0 любое целое число а можно представить в одном из следующих видов:
При этом если
Например, любое целое число можно представить в виде Любое целое число можно представить в виде Примеры: 1. Какой цифрой заканчивается число 3 Решение: Так как число 3
Какие остатки могут получиться при делении квадрата целого числа на 3? Решение: Всякое число a в соответствии с остатками от деления его на 3 может быть представлено в одном из видов: a=3k, a=3k+1, a=3k+2 (k–целое число). Соответственно получаем a Мы видим, что число a |
, то 
и 
делится на 
.
то q называется неполным частным, а r – остатком от деления a на b.
то будем иметь 
, если 
и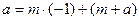
, если 
.
или 
.
, 
или 
.
?
оканчивается цифрой 1, то и любая его степень вида (3 
оканчивается цифрой 1. Найдём остаток от деления числа 1995 на 4. Имеем 1995=4×498+3. Значит, 3 
×3 
. Первый множитель оканчивается цифрой 1, а второй – цифрой 7. Значит, произведение оканчивается цифрой 7, то есть число 3 
=9k