 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Общая постановка двойственной задачи
Предположим, что некоторая организация решила закупить ресурсы Р1 , Р2 ,…, Рm фирмы; необходимо определить цены на ресурсы у1, у2,…, уm. Естественно, что покупающая организация заинтересована в том, чтобы затраты на покупку ресурсов в объеме b1, b2,…, bm по ценам у1, у2,…, уm были минимальны, то есть Z = b1y1 + b2y2 + … + bmym ® min. Предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная выручка была не меньше той суммы, которую предприятие может получить при переработке ресурсов в готовую продукцию. На изготовление единицы продукции j-го вида расходуется сырье Р1 в объеме а1j, сырье Р2 – в объеме а2j, сырье Рm – в объеме аmj по цене у1, у2,…, уm соответственно, то есть затраты на изготовление продукции Пj должны быть не меньше, чем цена ее реализации. Приходим к ограничениям следующего вида: а1jу1 + а2jу2 + … + аmjуm ≥ сj , j=1,2,...,n. С учетом условия неотрицательности цены единицы i-го ресурса приходим к нижеследующей задаче. Найти такой вектор У = (у1, у2 ,..., уm) цен ресурсов, удовлетворяющий системе неравенств
a12y1 + a22y2 + … + am2ym ≥ c2, … … … … … … … a1jy1 + a2jy2 + … + amjym ≥ cj, … … … … … … … a1ny1 + a2ny2 + … + amnym ≥ cn, yi ³ 0, i = 1, 2, …, m, при котором функция Z = b1y1 + b2y2 + …+ bmym принимает минимальное значение. Цены ресурсов в экономической литературе имеют различные названия: учетные, неявные, теневые, объективно-обусловленные оценки (о-о оценки) [11]. Это условные, ненастоящие цены; их называют оценками ресурсов и определяют в ходе решения задачи. Сопоставим общие представления прямой и двойственной задач в табл. 3, причем прямая задача – это задача модели распределения ограниченных ресурсов. Таблица 3
При сравнении рассмотренных примеров видно, что двойственная задача по отношению к исходной составляется согласно следующим правилам: 1. Если первая задача имеет размеры 2. Матрицы из коэффициентов при переменных в левых частях ограничений обеих задач являются взаимно транспонированными. З. В правых частях ограничений в каждой задаче стоят коэффициенты при переменных в целевой функции другой задачи. 4. В прямой задаче все ограничения представляют собой неравенства типа « Графически эти правила представлены в табл. 4.
Таблица 4
Экономическое содержание основной теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадение значений целевых функций для соответствующих планов пары двойственных задач достаточно для того, чтобы эти планы были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки отличаются тем, что гарантируют рентабельность оптимального плана, то есть равенство общей оценки продукции и ресурсов, и показывают убыточность всякого другого плана, отличного от оптимального. Из приведенных соотношений видно, что для всех допустимых решений прямой и двойственной задач значения целевой функции задачи минимизации всегда будет верхним пределом значения целевой функции задачи максимизации. Таким образом, итерационное решение задачи максимизации ведет к возрастанию значения целевой функции, а итерационное решение задач минимизации – к ее убыванию. В итоге при успешном завершении процессов вычисления прямой и двойственной задач приходят к точке «равновесия», где значения целевых функций задач максимизации и минимизации становятся равными. Имеет место следующая теорема равновесия, используя которую, можно находить решение одной из двойственных задач, зная решение другой задачи. Теорема равновесия. Пусть Х* – какое-нибудь допустимое решение прямой задачи, а Y* – какое-нибудь допустимое решение двойственной задачи. Для одновременной оптимальности этих решений необходимо и достаточно выполнение равенств
Величины, стоящие в скобках сформулированной теоремы, равны разности между левой и правой частями ограничения одной из двойственных задач на соответствующую переменную другой задачи. С учетом условий неотрицательности переменных и знаков сомножителей в произведениях можно получить следующее: если какое-либо ограничение одной задачи на оптимальном плане выполняется как строгое неравенство, то соответствующая координата оптимального плана другой задачи равна нулю: Если ai1 x1* + ai2 x2*+ ... + ain xn* < bi , то yi* = 0 . Если a1j y1* + a2j y2*+ … + amj ym* > cj , то xj* = 0 . Если какая-либо координата оптимального плана одной задачи положительна, то соответствующее ограничение другой задачи обращается в равенство: Если yi* > 0 , то ai1 x1* + ai2 x2*+ ... + ain xn* = bi . Если xj* > 0 , то a1j y1* + a2j y2*+ … + amj ym* = cj . Экономическое содержание теоремы равновесия означает, что если по некоторому оптимальному плану Х* производства расход i-го ресурса строго меньше его запаса bi, то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равно нулю. Если же в некотором оптимальном плане оценок его i-я координата больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда следует, что двойственные оценки служат мерой дефицитности ресурсов. Дефицитный ресурс, который полностью используется по оптимальному плану производства, имеет положительную оценку, а избыточный ресурс, не используемый полностью, имеет нулевую оценку. Пример 3.Используя теорему равновесия, решить пару двойственных задач (табл.5). Таблица 5
Решим прямую задачу графическим методом.
Рис. 6
Аналогично примеру 1 строим область допустимых решений, которая представляет собой выпуклый многоугольник ОАВСD. Нормаль линии уровня Определяем координаты точки С как пересечение прямых p1 и p2. Для этого решаем систему
Получаем:
Следовательно, координаты точки По основной теореме двойственности Z(Y*) = F(Х*) = 3. Подставим Х* = (4;1) в систему ограничений прямой задачи:
Первое ограничение прямой задачи на оптимальном плане выполняется как строгое неравенство, следовательно, соответствующая переменная двойственной задачи равна нулю: y1*= 0. Второе и третье ограничения прямой задачи обращаются в точное равенство, следовательно, соответствующие переменные двойственной задачи положительны: y2* > 0 и y3* > 0. Условия равновесия можно записать в виде равенств:
Следовательно
Подставляя y1*= 0 в последнюю систему уравнений, получим систему:
Откуда y2* = Оптимальное решение двойственной задачи Y*= (0; Графический способ решения задач показывает, что оптимальное решение задач, сводящихся к линейным моделям, всегда ассоциируется с угловой точкой области допустимых решений. Переход от геометрического способа решения задач к симплекс-методу лежит через алгебраическое описание угловых точек области допустимых решений. Для реализации этого перехода сначала надо привести задачу к канонической форме, преобразовав неравенства ограничений в равенства путем введения дополнительных переменных. Каноническаяформа задачи необходима, потому что позволяет получить базисное решение, которое полностью определяет все (геометрические) крайние точки пространства решений. Симплекс-метод дает возможность найти оптимальное решение среди всех базисных.
|



 a11у1 + a21у2 + … + am1уm ≥ c1,
a11у1 + a21у2 + … + am1уm ≥ c1, при ограничениях
при ограничениях  ; i=1, 2, ..., m xj ³ 0, j = 1, 2, …, n
; i=1, 2, ..., m xj ³ 0, j = 1, 2, …, n при ограничениях
при ограничениях 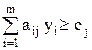 ; j = 1, 2, …, n yi ³ 0, i=1, 2, ..., m
; j = 1, 2, …, n yi ³ 0, i=1, 2, ..., m (m–ограничений с n переменными), то вторая – размеры
(m–ограничений с n переменными), то вторая – размеры  .
.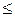 », причем в этой задаче требуется достичь
», причем в этой задаче требуется достичь  . Напротив, в двойственной задаче все ограничения суть неравенства типа «
. Напротив, в двойственной задаче все ограничения суть неравенства типа «  », причем требуется достичь
», причем требуется достичь 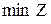 .
.
 при ограничениях
при ограничениях 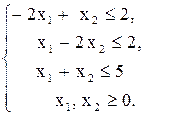
 при ограничениях
при ограничениях 













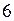



 (рис. 6).
(рис. 6).


 . Оптимальное решение х1* = 4, х2* = 1. Вычисляем максимум целевой функции прямой задачи:
. Оптимальное решение х1* = 4, х2* = 1. Вычисляем максимум целевой функции прямой задачи: 
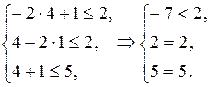



 , y3* =
, y3* =  .
.