ПОЗНАВАТЕЛЬНОЕ

Сила воли ведет к действию, а позитивные действия формируют позитивное отношение

Как определить диапазон голоса - ваш вокал

Игровые автоматы с быстрым выводом

Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими

Целительная привычка

Как самому избавиться от обидчивости

Противоречивые взгляды на качества, присущие мужчинам

Тренинг уверенности в себе

Вкуснейший "Салат из свеклы с чесноком"

Натюрморт и его изобразительные возможности

Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.

Как научиться брать на себя ответственность

Зачем нужны границы в отношениях с детьми?

Световозвращающие элементы на детской одежде

Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия

Как слышать голос Бога

Классификация ожирения по ИМТ (ВОЗ)

Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Классификация математических моделей

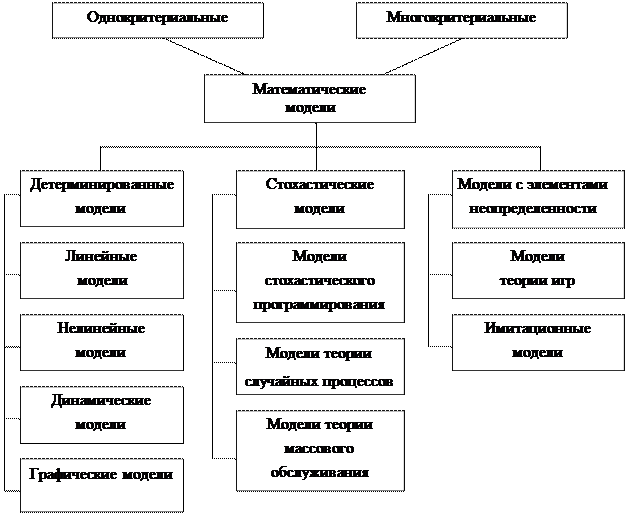
По числу критериев эффективности математические модели делятся на однокритериальные и многокритериальные (рис. 1). Многокритериальные матема-тические модели содержат два и более критерия.

По учету неизвестных факторов математические модели делятся на де­терминированные, стохастические и модели с элементами неопределен­ности.

Рис. 1

В стохастических моделях неизвестные факторы – это случайные величины, для которых известны функции распределения и различные статистические характеристики (математическое ожидание, дисперсия, среднеквадратическое отклонение и т. п.). Среди стохастических можно выделить:

· модели стохастического программирования,в которых либо в целе­вую функцию, либо в ограничения входят случайные величины;

· модели теории случайных процессов,предназначенные для изучения процессов, состояние которых в каждый момент времени является слу­чайной величиной;

· модели теории массового обслуживания,в которой изучаются много­канальные системы, занятые обслуживанием требований. К стохас­тическим моделям можно также отнести модели теории полезности, поиска и принятия решении.

Для моделирования ситуаций, зависящих от факторов, для которых не­возможно собрать статистические данные либо значения которых не опреде­лены, используются модели с элементами неопределенности. Вмоделях теории игрзадача представляется в виде игры, в которой участвуют несколько игроков, преследующих разные цели, например организацию предприятия в условиях конкуренции.

Вимитационных моделяхреальный процесс разворачивается в ма­шинном времени и прослеживаются результаты случайных воздействий на него, например организация производственного процесса.

В детерминированных моделях неизвестные факторы не учитываются. Несмотря на кажущуюся простоту этих моделей, к ним сводятся многие практические задачи, в том числе большинство социально-экономических задач. По виду целевой функции и ограничений детерминированные модели де­лятся на линейные, нелинейные, динамические и графические.

Влинейных моделяхцелевая функция и ограничения линейны по управляющим переменным. Построение и расчет линейных моделей яв­ляются наиболее развитым разделом математического моделирования, поэтому часто к ним стараются свести и другие задачи либо на этапе по­становки, либо в процессе решения. Для линейных моделей любого вида и достаточно большой размерности известны стандартные методы решения.

Нелинейные модели– это модели, в которых либо целевая функция, либо какое-нибудь из ограничений (либо все ограничения) не линейны по управляющим переменным. Для нелинейных моделей нет единого мето­да расчета. В зависимости от вида нелинейности, свойств функции и ог­раничений можно предложить различные способы решения. Однако мо­жет случиться и так, что для поставленной нелинейной задачи вообще не существует метода. В этом случае задачу следует упростить, либо сведя ее к из­вестным линейным моделям, либо просто линеаризовав модель.

В динамических моделяхв отличие от статических линейных и нели­нейных моделей учитывается фактор времени. Критерий оптимальности в динамических моделях может быть самого общего вида (и даже вообще не быть функцией), однако для него должны выполняться определенные свойства. Расчет динамических моделей сложен, и для каждой конкрет­ной задачи необходимо разрабатывать специальный алгоритм решения.

Графические моделииспользуются тогда, когда задачу удобно пред­ставить в виде графической структуры.

Основные этапы построения модели:

1. Определение цели, т.е. чего хотят добиться, решая поставленную задачу.

2. Определение параметров модели, т.е. заранее известных фикси­рованных факторов, на значения которых исследователь не влияет.

3. Формирование управляющих переменных, изменяя значение которых можно приближаться к поставленной цели. Значения управляющих переменных являются решениями задачи.

4. Определение области допустимых решений, т.е. тех ограничений, которым должны удовлетворять управляющие переменные.

5. Выявление неизвестных факторов, т.е. величин, которые могут изменяться случайным или неопределенным образом.

6. Выражение цели через управляющие переменные, параметры и неизвестные факторы, т.е. формирование целевой функции, на­зываемой также критерием эффективности или критерием оп­тимальности задачи.

Линейные модели

Линейные модели имеют широкое применение при решении экономических задач, возникающих в производстве, управлении финансами, торговле, транспортной отрасли и т.д. Построение линейных моделей является наиболее развитым разделом математического моделирования.

Широкое применение линейных моделей любого вида и достаточно большой размерности подкрепляется высокоэффективными компьютерными алгоритмами.