 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Двойственность и основные соотношения двойственности
К моделям линейной оптимизации относятся задачи на максимум или минимум линейной целевой функции многих переменных при ограничениях на них в форме линейных равенств и неравенств. С любой экономико-математической задачей, для которой можно построить линейную модель, либо свести к построению линейной модели, связана двойственная задача. Прямая и двойственная задачи тесно взаимосвязаны, так как оптимальное решение одной задачи можно получить непосредственно, зная оптимальное решение другой задачи. Совместное изучение прямой задачи и двойственной к ней дает, как правило, значительно больше информации. Рассмотрим решения прямой и двойственной задач графическим методом, с помощью которого легко иллюстрируются основные соотношения теории двойственности. Пример 1. Решить графическим методом прямую и двойственную задачи (табл. 1). Таблица 1
Решение прямой задачи.Строим область допустимых решений задачи. Для этого нумеруем ограничения задачи
В прямоугольной декартовой системе координат (рис. 2) строим прямую
Находим общую часть полуплоскостей решений, учитывая при этом условия неотрицательности переменных. Полученная область допустимых решений на рисунке заштрихована и представляет собой ограниченный выпуклый многоугольник ОАВС. Строим нормаль линий уровня Определяем координаты точки В как пересечение прямых p1 и p2. Для этого решаем систему
Получаем:
Следовательно, координаты точки Решение двойственной задачи. Для построения области допустимых решений занумеруем ограничения задачи:
Строим прямые p3 и p4, уравнения которых: – 2у1 + у2 = 2 и 3у1 + у2 = 7. Учитывая условия неотрицательности переменных, определяем область допустимых решений. Полученная область представляет собой неограниченный сверху выпуклый многоугольник (рис. 3). Нормаль линии уровня
В данной задаче необходимо найти минимум целевой функции, поэтому линию уровня перемещаем в направлении, противоположном направлению нормали до опорной прямой. Эта прямая проходит через точку D пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (3) и (4), перпендикулярно нормали. Определяем координаты точки D как пересечение прямых p3 и p4. Для этого решаем систему
Получаем, что точка D имеет координаты
Как видно из приведенных решений прямой и двойственной задач, значения целевых функций равны: При любом допустимом решении прямой задачи значение целевой функции « Например, при допустимом решении прямой задачи
Пример 2. Решить графическим методом прямую и двойственную задачи (табл. 2). Таблица 2
Для решения прямой задачи вводим нумерацию ограничений задачи:
Аналогично примеру 1 строим область допустимых решений, которая представляет собой выпуклый многоугольник, не ограниченный сверху. Нормаль линии уровня В данной задаче необходимо найти минимум целевой функции, поэтому линию уровня перемещаем в направлении, противоположном направлению нормали, которая уходит в бесконечность. Задача не имеет оптимального решения из-за неограниченности снизу целевой функции
Решение двойственной задачи:
Область допустимых решений для данной задачи представляет собой пустое множество, что означает противоречивость системы ограничений (рис. 5). Следовательно, и двойственная задача так же, как и прямая задача, не имеет решения.
Взаимозависимость оптимальных решений пары двойственных задач определена следующими соотношениями: Теорема (основное неравенство). Пусть Х – какое-нибудь допустимое решение прямой задачи, а Y – какое-нибудь допустимое решение двойственной задачи. Тогда справедливо неравенство
Следствие 1 (достаточный признак оптимальности). Если для каких-то допустимых решений
то Следствие 2. Если в одной из пары двойственных задач целевая функция не ограничена с соответствующей стороны (т.е. Основная теорема. Если разрешима одна из пары двойственных задач, то разрешима и другая задача, причем Остальные теоремы двойственности будут сформулированы в следующих разделах данного пособия. Для понимания экономической интерпретации основных соотношений двойственности рассмотрим модель распределения ограниченных ресурсов, в которой целевая функция, отображающая прибыль или доход от производственной деятельности, подлежит максимизации.
|



 при ограничениях
при ограничениях 
 при ограничениях
при ограничениях 

 (p1), соответствующую ограничению (1) по двум точкам, например, (– 7; 0) и (– 4; 2). Находим, какая из полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая p1 не проходит через начало координат, подставляем координаты точки
(p1), соответствующую ограничению (1) по двум точкам, например, (– 7; 0) и (– 4; 2). Находим, какая из полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая p1 не проходит через начало координат, подставляем координаты точки  в первое ограничение
в первое ограничение 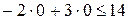 . Получаем строгое неравенство
. Получаем строгое неравенство  . Следовательно, точка О лежит в полуплоскости решений. Штриховкой отмечаем полуплоскость, содержащую точку О. Аналогично строим прямую
. Следовательно, точка О лежит в полуплоскости решений. Штриховкой отмечаем полуплоскость, содержащую точку О. Аналогично строим прямую  (p2) по двум точкам (0; 8) и (8; 0) и определяем область решений ограничения (2).
(p2) по двум точкам (0; 8) и (8; 0) и определяем область решений ограничения (2).



















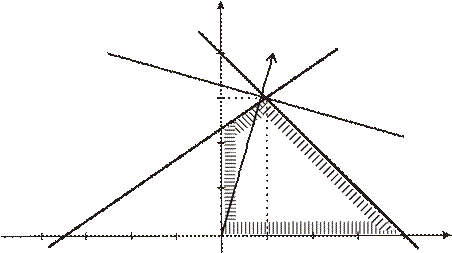
 . Так как решается задача на отыскание максимума целевой функции, то линию уровня
. Так как решается задача на отыскание максимума целевой функции, то линию уровня  перемещаем в направлении нормали до угловой точки В, которая расположена на прямой, называемой опорной. Эта опорная прямая проходит через точку В пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (1) и (2), перпендикулярно нормали.
перемещаем в направлении нормали до угловой точки В, которая расположена на прямой, называемой опорной. Эта опорная прямая проходит через точку В пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (1) и (2), перпендикулярно нормали.


 . Оптимальное решение х1* = 2, х2* = 6. Вычисляем максимум целевой функции:
. Оптимальное решение х1* = 2, х2* = 6. Вычисляем максимум целевой функции:  Уравнение опорной прямой имеет вид
Уравнение опорной прямой имеет вид  .
.
 .
.
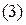


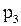






 . Оптимальное решение у1* = 1, у2* = 4. Вычисляем минимум целевой функции:
. Оптимальное решение у1* = 1, у2* = 4. Вычисляем минимум целевой функции:  Уравнение опорной прямой имеет вид
Уравнение опорной прямой имеет вид  .
.
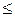 » (не превосходят) значений целевой функции двойственной задачи при ее допустимом произвольном решении.
» (не превосходят) значений целевой функции двойственной задачи при ее допустимом произвольном решении. значение целевой функции
значение целевой функции  , а при допустимом двойственной задачи
, а при допустимом двойственной задачи  значение целевой функции
значение целевой функции  , т.е.
, т.е.  .
. при ограничениях
при ограничениях 
 при ограничениях
при ограничениях 

 (рис. 4).
(рис. 4). на множестве допустимых решений.
на множестве допустимых решений.
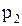



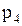

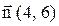

 .
. и
и  соответственно прямой и двойственной задач выполняется равенство
соответственно прямой и двойственной задач выполняется равенство ,
, в прямой задаче или
в прямой задаче или  в двойственной задаче), то другая задача не имеет допустимых решений.
в двойственной задаче), то другая задача не имеет допустимых решений. .
.