 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Угол между прямыми. Расстояние от точки до прямой.
Углом между прямыми называется наименьший из смежных углов, образованных при пересечении прямых.
Расстояние от точки до прямой: Линии второго порядка на плоскости: окружность, эллипс, гипербола, парабола; их канонические уравнения, характеристики. Общее уравнение линии второго порядка имеет следующий вид: Ax2 + By2 + Cxy + Dx + Ey + F = 0. 1) Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. Уравнение эллипса в каноническом виде: Форма эллипса зависит от отношения Окружностью радиуса R с центром в точке M0 называется множество всех точек Μ плоскости, удовлетворяющих условию М0М = R.
Характеристики: Эксцентриситет: 2a – большая полуось 2b – меньшая полуось Фокусы: (с,0); (-с,0) 2) Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами. Уравнение гиперболы в каноническом виде: Характеристики:
Асимптоты: 3) Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через p (p > 0).
Уравнение параболы в каноническом виде: Виды парабол:
Характеристики: Директриса: Эксцентриситет: всегда равен 1
Общее уравнение линий второго порядка: уравнение кривых, оси симметрии которых параллельны осям координат; общее уравнение второго порядка.
Эллипс
с большой полуосью «а», малой полуосью «бэ» и центром симметрии в точке Гипербола
с действительной полуосью «а», мнимой полуосью «бэ» и центром в точке Порабола
Порабола со смещенным центром. Если перед 2р стоит «-», то порабола перевернутая
Поверхность и её уравнение. Уравнение линий в пространстве. Общее уравнение плоскости
Плоскость в пространстве и её уравнение: уравнения плоскости, проходящеё через данную точку перпендикулярно данному вектору; общее уравнение плоскости; уравнение плоскости, проходящеё через три точки; уравнение плоскости в отрезках. Общее уравнение плоскости
проходящей через точку Уравнение плоскости, проходящей через три точки
Уравнение плоскости в отрезках
Угол между плоскостями; расстояние от точки до плоскости. · Углом между плоскостями называется наименьший из двугранных углов, образованных при пересечении плоскостей.
Расстояние от точки до плоскости
Так как точка Тогда В частности: |



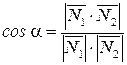 .
. .
.
 . При
. При  эллипс превращается в окружность
эллипс превращается в окружность







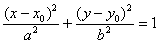

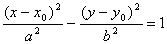








 , перпендикулярно вектору
, перпендикулярно вектору 
 .
.
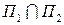
 или
или  ,
,  .
.
 :
:  ,
,  .
. 

 , то
, то  , т.е.
, т.е. 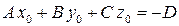 .
.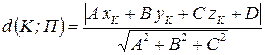 .
. .
.