 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Скалярное произведение векторов, его свойства. Выражение скалярного произведения через координаты перемножаемых векторов.
· Скалярным произведением векторов
Свойства скалярного произведения (следуют из определения): 1) 2) 3) 4) 5) 6) 4. Векторное произведение двух векторов, его свойства. Выражение векторного произведения через координаты перемножаемых векторов. · Векторным произведением векторов
1) длина которого равна площади параллелограмма, построенного на векторах 2) направлен он перпендикулярно плоскости этого параллелограмма так, что вектора Свойства векторного произведения (следуют из определения): 1) 2) 3) 2. 3. 4) 5) 6) Замечание. 1) Если
2) Если
Координатная форма векторного произведения:
Или 5. Смешанное произведение векторов, его геометрический смысл, свойства. Смешанное произведение в координатной форме. · Смешанным произведением трёх векторов
Свойства смешанного произведения. (следуют из определения и свойств скалярного и векторного произведений). 1) При перестановке двух векторов смешанное произведение меняет свой знак:
2) При циклической перестановке трёх векторов смешанное произведение сохраняет свой знак: 3) 4) Координатная форма смешанного произведения:
Теорема (критерий компланарности векторов) Векторы ►1) Если среди компланарных векторов есть коллинеарные, то их координаты пропорциональны. Следовательно, определитель, составленный из координат векторов, будет равен нулю. Если среди компланарных векторов, принадлежащих плоскости Т. е. 2) Пусть Т. к. при этом 6. Приложения скалярного, векторного и смешанного произведения векторов. Приложения скалярного произведения: 1. Определение косинуса угла между векторами:
2. Нахождение проекции вектора на заданное направление:
Приложения векторного произведения: 1. Установление коллинеарности векторов: (
2. Нахождение площади параллелограмма и треугольника:
Приложения смешанного произведения: 1. Определение взаимной ориентации векторов в пространстве. Если 2. Установление компланарности векторов:
(
3. Определение объема параллелепипеда и треугольной пирамиды (тетраэдра):
Элементы аналитической геометрии на плоскости и в пространстве Линии на плоскости. Уравнения прямой на плоскости: с угловым коэффициентом; общее уравнение прямой; уравнение прямой, проходящей через точку в данном направлении, через две точки; уравнение прямой в отрезках; полярное уравнение прямой; нормальное уравнение прямой. Линией на плоскости называется ГМТ плоскости, координаты которых удовлетворяют уравнению связи двух переменных. Способы задания уравнения линии: − неявно − явно − параметрически − в полярных координатах Уравнение прямой на плоскости: 1) с угловым коэффициентом: 2) 3) Уравнение прямой, проходящей через точку в данном направлении: 4) Уравнение прямой, проходящей через две точки: 5) Уравнение прямой в отрезках: 6) Полярное уравнение прямой: 7) |



 и
и  называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними: .
.


 − коммутативность.
− коммутативность. −дистрибутивность.
−дистрибутивность. .
. и
и  называется вектор
называется вектор ,
, образуют правую тройку векторов.
образуют правую тройку векторов. .
.
 В частности: 1.
В частности: 1. 


 − антикоммутативность.
− антикоммутативность. − дистрибутивность.
− дистрибутивность. .
. и
и  , то
, то .
. ,
,  ,
,  , то
, то .
.





 .
. .
. .
. − антикоммутативность.
− антикоммутативность. .
. .
. .
.


 .
. – компланарны
– компланарны 
 .
.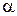 , нет коллинеарных, то
, нет коллинеарных, то  .
. .
.
 .
. , то векторы
, то векторы 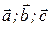 параллельны одной и той же плоскости, т. е. компланарны.
параллельны одной и той же плоскости, т. е. компланарны. .
. ,
, 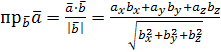 .
. (
(  ), т.е.
), т.е.
 ,
, 
 ,
,  и
и  – правая тройка, если
– правая тройка, если 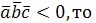 левая.
левая. Þ (
Þ (  ,
, 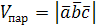 ,
,  .
. ;
;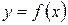 ;
;
 .
.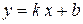
 − общее уравнение прямой, проходящей через точку
− общее уравнение прямой, проходящей через точку  , перпендикулярно вектору
, перпендикулярно вектору  .
. .
. .
. .
.
 − каноническое уравнение прямой, проходящей через точку
− каноническое уравнение прямой, проходящей через точку  .
.