 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Вычисление определителя n-ого порядка
Примеры. 1. Найти произведения матриц Решение:
2. Даны матрицы Решение:
2. Определители, их свойства. Миноры и алгебраические дополнения. Вычисление определителя порядков 2, 3, «n». Определитель квадратной матрицы · Определителем (детерминантом) матрицы Обозначение: Размерность матрицы определяет порядок определителя.
Свойства: 1. При транспонировании матрицы её определитель не изменяется:
2. При перестановке двух строк (столбцов) определитель меняет знак:
3. При умножении элементов строки (столбца) определителя на некоторое число весь определитель умножается на это число: Следствие: Общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя. 4. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число: 5. Определитель, имеющий нулевую строку (столбец), равен 0: Следствие: Определитель, имеющий две равные строки (столбца) или две пропорциональные строки (столбца), равен 0: 6. 7. 8. Если для элементов какой-либо строки или столбца матрицы верно соотношение:
Доказательства этих свойств следуют из правил вычисления определителя и справедливы для определителей любого порядка. Например докажем свойство №3 для определителя 2-ого порядка:
Вычисление определителя n-ого порядка · Минором элемента Пример: Для элемента
· Алгебраическим дополнением элемента Обозначение: Пример: Для элемента
Теорема 1 Определитель равен сумме произведений элементов любой его строки или столбца на соответствующие им алгебраические дополнения:
► Докажем теорему для определителя 3-ого порядка. Для матрицы
Теорема 2. Сумма произведений элементов строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю. ►Алгебраические дополнения Например, алгебраические дополнения
− элементы 1-ой строки заменились элементами 2-ой строки. Т. о. полученный определитель будет иметь две одинаковые (i-ые) строки. По свойствам значение такого определителя равно нулю. ■ Вывод: Замечание. Для разложения определителя обычно выбирают ту строку или тот столбец, где есть нулевые элементы, так как соответствующие им слагаемые в разложении будут равны нулю.
|



 и
и  .
. ×
×  =
= 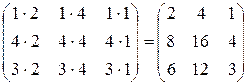 .
. ×
×  = (2×1 + 4×4 + 1×3) = (21).
= (2×1 + 4×4 + 1×3) = (21). ,
,  ,
,  . Найти
. Найти 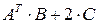 .
. ;
;  ;
;
 ×
×  =
=  =
=  ;
;
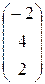 =
= 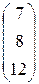 .
. называется число, равное значению алгебраического выражения, составленного по определённому правилу для элементов данной матрицы.
называется число, равное значению алгебраического выражения, составленного по определённому правилу для элементов данной матрицы. .
.
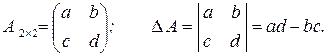



 «правило треугольников»:
«правило треугольников»:  –
–  Пример:
Пример: .
. .
. .
. .
.
 .
.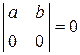
 ,
,  .
. .
. .
. ,
,  ,
,  , то верно:
, то верно: .
. .
. определителя
определителя  -ого порядка называется определитель
-ого порядка называется определитель  -ого порядка, полученный из исходного путем вычеркивания
-ого порядка, полученный из исходного путем вычеркивания  -ой строки и
-ой строки и  -ого столбца (на пересечении которых находится выбранный элемент). Обозначение:
-ого столбца (на пересечении которых находится выбранный элемент). Обозначение:  .
. определителя
определителя  имеем
имеем 
 », если сумма
», если сумма  – четна, в противном случае со знаком «–».
– четна, в противном случае со знаком «–». .
.
 (по
(по  (по
(по  составим и преобразуем сумму произведений элементов 1-ой его строки на соответствующие им алгебраические дополнения:
составим и преобразуем сумму произведений элементов 1-ой его строки на соответствующие им алгебраические дополнения:




 . ■
. ■ элементов квадратной таблицы чисел содержат все строки (в том числе и i-ую строку) исходной таблицы чисел, кроме k-ой строки. Суммирование
элементов квадратной таблицы чисел содержат все строки (в том числе и i-ую строку) исходной таблицы чисел, кроме k-ой строки. Суммирование 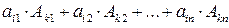 определяет значение определителя квадратной таблицы чисел, полученной из исходной заменой элементов k-ой строки соответствующими элементами i-ой строки.
определяет значение определителя квадратной таблицы чисел, полученной из исходной заменой элементов k-ой строки соответствующими элементами i-ой строки. элементов квадратной таблицы чисел размерности
элементов квадратной таблицы чисел размерности  содержат элементы 2-ой и 3-ей строк. Тогда:
содержат элементы 2-ой и 3-ей строк. Тогда: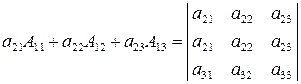 −
−
 .
.