 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Условие существования обратной матрицы
· Квадратнаяматрица называется невырожденной, если её определитель не равен нулю. В противном случае матрица называется вырожденной. · Матрицей, союзной к матрице А, называется транспонированная матрица алгебраических дополнений элементов аij данной матрицы:
Теорема. Всякая невырожденная матрица имеет обратную, при этом ►Проведем доказательство для случая матрицы 3-го порядка. Пусть
Умножая слева обе части равенства на матрицу
Для элементов невырожденной матрицы
Тогда
| ||
Обратная матрица · Матрица B называется обратной к матрице 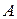 , если справедливо равенство: , если справедливо равенство:  . Обозначение: . Обозначение:  − Только квадратная матрица может иметь обратную матрицу. − Не всякая квадратная матрица имеет обратную матрицу. Свойства: 1. − Только квадратная матрица может иметь обратную матрицу. − Не всякая квадратная матрица имеет обратную матрицу. Свойства: 1.  ; 2. ; 2.  ; 3. ; 3.  , где матрицы , где матрицы  −квадратные, одинаковой размерности. Вообще говоря, если для не квадратных матриц −квадратные, одинаковой размерности. Вообще говоря, если для не квадратных матриц  возможно произведение возможно произведение  , которое будет являться квадратной матрицей, то возможно существование и обратной матрицы , которое будет являться квадратной матрицей, то возможно существование и обратной матрицы  ,хотя 3-свойство при этом нарушается. Для нахождения обратной матрицы можно использовать метод элементарных преобразований строк: 1. Составляют расширенную матрицу, приписывая справа от исходной матрицы единичную матрицу соответствующей размерности: ,хотя 3-свойство при этом нарушается. Для нахождения обратной матрицы можно использовать метод элементарных преобразований строк: 1. Составляют расширенную матрицу, приписывая справа от исходной матрицы единичную матрицу соответствующей размерности:  . 2. Элементарными преобразованиями строк матрицу Г приводят к виду: . 2. Элементарными преобразованиями строк матрицу Г приводят к виду:  . .  − искомая Ранг матрицы · Минором k-ого порядка матрицы − искомая Ранг матрицы · Минором k-ого порядка матрицы  называется определитель, составленный из элементов исходной матрицы, стоящих на пересечении любых k строк и k столбцов ( называется определитель, составленный из элементов исходной матрицы, стоящих на пересечении любых k строк и k столбцов (  ). Замечание. Каждый элемент матрицы является ее минором 1-го порядка. Теорема. Если в матрице все миноры k-ого порядка равны нулю, то равны нулю все миноры большего порядка. ►Разложим минор (определитель) (k+1)-ого порядка через элементы 1-ой строки: ). Замечание. Каждый элемент матрицы является ее минором 1-го порядка. Теорема. Если в матрице все миноры k-ого порядка равны нулю, то равны нулю все миноры большего порядка. ►Разложим минор (определитель) (k+1)-ого порядка через элементы 1-ой строки:  . Алгебраические дополнения по сути являются минорами k-ого порядка, которые по условию теоремы равны нулю. Следовательно, . Алгебраические дополнения по сути являются минорами k-ого порядка, которые по условию теоремы равны нулю. Следовательно,  . · В матрице порядка . · В матрице порядка  минор порядка минор порядка  называется базисным, если он не равен нулю, а все миноры порядка называется базисным, если он не равен нулю, а все миноры порядка  и выше равны нулю, или не существуют вовсе, т.е. и выше равны нулю, или не существуют вовсе, т.е.  совпадает с меньшим из чисел совпадает с меньшим из чисел  или или  . Столбцы и строки матрицы, из которых стоит базисный минор, называются базисными. В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок. · Порядок базисного минора матрицы называется рангом матрицыи обозначается: . Столбцы и строки матрицы, из которых стоит базисный минор, называются базисными. В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок. · Порядок базисного минора матрицы называется рангом матрицыи обозначается:  , ,  . Очевидно, что . Очевидно, что  . Например. 1. . Например. 1. 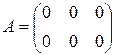 , ,  . 2. . 2.  . Матрица В содержит единственный ненулевой элемент . Матрица В содержит единственный ненулевой элемент  являющийся минором 1-го порядка. Все определители более высоких порядков будут содержать 0-ю строку и поэтому равны 0. Следовательно, являющийся минором 1-го порядка. Все определители более высоких порядков будут содержать 0-ю строку и поэтому равны 0. Следовательно, 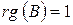 . обратная матрица . обратная матрица  4. Системы линейных уравнений. Основные понятия. Система линейных алгебраических уравнений (линейная система, также употребляются аббревиатуры СЛАУ, СЛУ) — система уравнений, каждое уравнение в котором является линейным — алгебраическим уравнением первой степени. Общий вид системы линейных алгебраических уравнений: 4. Системы линейных уравнений. Основные понятия. Система линейных алгебраических уравнений (линейная система, также употребляются аббревиатуры СЛАУ, СЛУ) — система уравнений, каждое уравнение в котором является линейным — алгебраическим уравнением первой степени. Общий вид системы линейных алгебраических уравнений:  Здесь Здесь  — количество уравнений, а — количество уравнений, а  — количество переменных, — количество переменных,  — неизвестные, которые надо определить, коэффициенты — неизвестные, которые надо определить, коэффициенты  и свободные члены и свободные члены  предполагаются известными. Система называется однородной, если все её свободные члены равны нулю ( предполагаются известными. Система называется однородной, если все её свободные члены равны нулю (  ), иначе — неоднородной. Решение системы линейных алгебраических уравнений — совокупность ), иначе — неоднородной. Решение системы линейных алгебраических уравнений — совокупность  чисел чисел  , таких что из соответствующая подстановка вместо , таких что из соответствующая подстановка вместо  в систему обращает все её уравнения в тождества. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. Решения считаются различными, если хотя бы одно из значений переменных не совпадает. Совместная система с единственным решением называется определённой, при наличии более одного решения — недоопределённой. Матричная форма Система линейных алгебраических уравнений может быть представлена в матричной форме как: в систему обращает все её уравнения в тождества. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. Решения считаются различными, если хотя бы одно из значений переменных не совпадает. Совместная система с единственным решением называется определённой, при наличии более одного решения — недоопределённой. Матричная форма Система линейных алгебраических уравнений может быть представлена в матричной форме как:  или: или:  . Здесь . Здесь  — это матрица — это матрица  системы, системы, 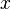 — столбец неизвестных, а — столбец неизвестных, а  — столбец свободных членов. Если к матрице приписать справа столбец свободных членов, то получившаяся матрица называется расширенной. Теорема Кронекера — Капелли Теорема Кронекера — Капелли устанавливает необходимое и достаточное условие совместности системы линейных алгебраических уравнений посредством свойств матричных представлений: система совместна тогда и только тогда, когда ранг её матрицы совпадает с рангом расширенной матрицы. Методы решения систем линейных уравнений. Матричный метод Пусть дана система линейных уравнений с — столбец свободных членов. Если к матрице приписать справа столбец свободных членов, то получившаяся матрица называется расширенной. Теорема Кронекера — Капелли Теорема Кронекера — Капелли устанавливает необходимое и достаточное условие совместности системы линейных алгебраических уравнений посредством свойств матричных представлений: система совместна тогда и только тогда, когда ранг её матрицы совпадает с рангом расширенной матрицы. Методы решения систем линейных уравнений. Матричный метод Пусть дана система линейных уравнений с  неизвестными (над произвольным полем): неизвестными (над произвольным полем):  Перепишем в матричной форме: Перепишем в матричной форме:  Решение системы найдем по формуле Решение системы найдем по формуле  Обратную матрицу найдем по формуле: Обратную матрицу найдем по формуле:  , где , где  – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  . Если . Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом Гаусса. Метод Крамера Ме́тод Крамера (правило Крамера) — способ решения СЛАУ с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы. Для системы , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом Гаусса. Метод Крамера Ме́тод Крамера (правило Крамера) — способ решения СЛАУ с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы. Для системы  линейных уравнений с линейных уравнений с  неизвестными неизвестными  Заменяем i-тый столбец матрицы столбцом свободных членов b Пример: Система линейных уравнений с вещественными коэффициентами: Заменяем i-тый столбец матрицы столбцом свободных членов b Пример: Система линейных уравнений с вещественными коэффициентами:  Определители: Определители:  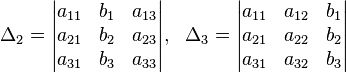 В определителях столбец коэффициентов при соответствующей неизвестной заменяется столбцом свободных членов системы. Решение: В определителях столбец коэффициентов при соответствующей неизвестной заменяется столбцом свободных членов системы. Решение:  5. Метод Гаусса Алгоритм решения: 1. Запишем расширенную матрицу 2. Приведем к ступенчатому виду путем элементарных преобразований 3. Обратный ход, в ходе которого выражаем базисные члены через свободные. Расширенная матрица получается путем добавления к матрице столбца свободных членов. Существуют следующие элементарные преобразования: 1. Строки матрицы можно переставлять местами. 2. Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. 3. Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить. 4. Строку матрицы можно умножить (разделить)на любое число, отличное от нуля. 5. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Элементарные преобразования не меняют решение системы уравнений Обратный ход: Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на "ступеньках". Далее выражаются базисные члены через свободные. Идем “снизу в вверх” попутно выражая базисные члены и подставляя результаты в вышестоящее уравнение. Пример: 5. Метод Гаусса Алгоритм решения: 1. Запишем расширенную матрицу 2. Приведем к ступенчатому виду путем элементарных преобразований 3. Обратный ход, в ходе которого выражаем базисные члены через свободные. Расширенная матрица получается путем добавления к матрице столбца свободных членов. Существуют следующие элементарные преобразования: 1. Строки матрицы можно переставлять местами. 2. Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. 3. Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить. 4. Строку матрицы можно умножить (разделить)на любое число, отличное от нуля. 5. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Элементарные преобразования не меняют решение системы уравнений Обратный ход: Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на "ступеньках". Далее выражаются базисные члены через свободные. Идем “снизу в вверх” попутно выражая базисные члены и подставляя результаты в вышестоящее уравнение. Пример:  Базисные переменные всегда «сидят» строго на ступеньках матрицы. В данном примере базисными переменными являются Базисные переменные всегда «сидят» строго на ступеньках матрицы. В данном примере базисными переменными являются  и и  Свободные переменные – это все оставшиеся переменные, которым не досталось ступеньки. В нашем случае их две: Свободные переменные – это все оставшиеся переменные, которым не досталось ступеньки. В нашем случае их две:  – свободные переменные. Теперь нужно все базисные переменные выразить только через свободные переменные. Обратный ход алгоритма Гаусса традиционно работает снизу вверх. Из второго уравнения системы выражаем базисную переменную – свободные переменные. Теперь нужно все базисные переменные выразить только через свободные переменные. Обратный ход алгоритма Гаусса традиционно работает снизу вверх. Из второго уравнения системы выражаем базисную переменную  : :  Теперь смотрим на первое уравнение: Теперь смотрим на первое уравнение:  . Сначала в него подставляем найденное выражение . Сначала в него подставляем найденное выражение  : :  Осталось выразить базисную переменную Осталось выразить базисную переменную  через свободные переменные через свободные переменные  : :  В итоге получилось то, что нужно – все базисные переменные ( В итоге получилось то, что нужно – все базисные переменные (  и и  ) выражены только через свободные переменные ) выражены только через свободные переменные  : : 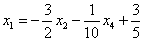  6. Системы линейных однородных уравнений Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например: 6. Системы линейных однородных уравнений Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например:  Однородная система всегда совместна, то есть всегда имеет решение. Однородная система линейных уравнений имеет только тривиальное решение Однородная система всегда совместна, то есть всегда имеет решение. Однородная система линейных уравнений имеет только тривиальное решение 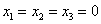 , если ранг матрицы системы равен количеству переменных. Фундаментальная система решений · Решения СЛУ: , если ранг матрицы системы равен количеству переменных. Фундаментальная система решений · Решения СЛУ:   ..., ...,  называются линейно независимыми, если их линейная комбинация называются линейно независимыми, если их линейная комбинация  дает нулевой столбец-вектор только при дает нулевой столбец-вектор только при  Число (k) линейно независимых решений совместной СЛОУ равно Число (k) линейно независимых решений совместной СЛОУ равно  , где r − ранг матрицы. · Любые , где r − ранг матрицы. · Любые  ЛНЗ-решений СЛОУ называются ее фундаментальной системой решений (ФСР). Пример: Однородная система линейных алгебраических уравнений ЛНЗ-решений СЛОУ называются ее фундаментальной системой решений (ФСР). Пример: Однородная система линейных алгебраических уравнений  с помощью элементарных преобразований может быть приведена к каноническому виду: с помощью элементарных преобразований может быть приведена к каноническому виду:  Ранг r матрицы равен 2, число n неизвестных равно 5, система нетривиально совместна. Размерность пространства решений этой однородной системы равна 3: d = n − I = 5 − 2 = 3. три линейно независимые решения системы Ранг r матрицы равен 2, число n неизвестных равно 5, система нетривиально совместна. Размерность пространства решений этой однородной системы равна 3: d = n − I = 5 − 2 = 3. три линейно независимые решения системы  образуют базис пространства решений системы, т.е. образуют её фундаментальную систему решений. образуют базис пространства решений системы, т.е. образуют её фундаментальную систему решений. |
Элементы векторной алгебры
Векторы. Основные понятия
· Вектором (в узком смысле) называется направленный отрезок:  .
.
· Вектором (в широком смысле) называется совокупность всех направленных отрезков, имеющих одинаковую длину и направление:  .
.
Нулевой вектор– это вектор, длина которого равна нулю:  .
.
Единичный вектор – это вектор, длина которого равна единице:  .
.
· Ортом вектора  называется единичный вектор, имеющий направление вектора
называется единичный вектор, имеющий направление вектора 
 .
.
· Двавектора называются коллинеарными, если они расположены на одной или параллельных прямых:  .
.




 .
. .
. . Составим союзную матрицу А*=
. Составим союзную матрицу А*=  и найдем произведение:
и найдем произведение: 


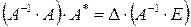


 . ■
. ■ найдём алгебраические дополнения:
найдём алгебраические дополнения:  ,
,  ,
,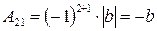 ,
,  .
. .
.  .
.