 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Методи оптимізації та дослідження операцій
. Підприємство електронної промисловості виготовляє дві моделі радіоприймачів, причому кожна модель складається на окремій технологічній лінії. Добовий обсяг виробництва першої лінії становить 60, а другої — 70 од. На один радіоприймач першої моделі витрачається 10 однотипних елементів електронних схем, а на радіоприймач другої моделі — 8. Максимальний добовий запас елементів, що використовуються у виробництві, становить 1000 од. Прибуток від реалізації одного радіоприймача першої та другої моделі дорівнює відповідно 35 та 25 дол. Визначити оптимальні обсяги виробництва радіоприймачів обох моделей.
2. Невелике сільськогосподарське підприємство спеціалізується на вирощуванні овочів, зокрема капусти та томатів, використовуючи для цього мінеральні добрива (фосфорні та калійні). Норми внесення мінеральних добрив під кожну культуру та запас добрив у господарстві наведено в таблиці:
Під вирощування овочів відведено земельну ділянку площею 20 га. Очікуваний прибуток господарства від реалізації 1 ц капусти становить 10 ум. од., а 1 ц томатів — 20 ум. од. Середня врожайність капусти в господарстві дорівнює 300 ц/га, а томатів — 200 ц/га. Визначити такий варіант розміщення культур на земельній ділянці, який максимізує прибуток господарства за умови, що витрати мінеральних добрив не перевищують максимально можливого запасу. 3. Фірма виготовляє два види продукції А та В, використовуючи для цього два види сировини, добовий запас якої має не перевищувати відповідно 210 та 240 ум. од. Витрати сировини для виготовлення одиниці продукції кожного виду подано таблицею:
Відділ збуту фірми вважає, що виробництво продукції В має становити не більш як 65 % загального обсягу реалізації продукції обох видів. Ціна одиниці продукції А та В дорівнює відповідно 10 та 40 дол. Визначити оптимальний план виробництва продукції, який максимізує дохід фірми.
4. Розв’язати транспортну задачу:
якщо вартість зберігання одиниці невивезеної продукції у постачальників А1, А2, А3, А4 дорівнює відповідно 5, 4, 2 та 3 ум. од. 5. Визначити оптимальний план такої транспортної задачі:
Висунуто таку вимогу: попит третього споживача має задовольнятися повністю. 6. Визначити оптимальний план транспортної задачі:
якщо ресурси четвертого постачальника потрібно використати повністю і за маршрутом А4В3 перевезти 20 од. продукції.
7. Розв’язати задачу симплекс-методом:
8. Записати двоїсту до наведеної задачі. Розв’язати одну із задач, визначити оптимальний план іншої задачі:
9. Записати двоїсту до наведеної задачі. Розв’язати одну із задач, визначити оптимальний план іншої задачі:
10. Записати двоїсту до наведеної задачі. Розв’язати одну із задач, визначити оптимальний план іншої задачі:
Математична статистика Аналіз даних
1. Побудувати кореляційне поле. Обчислити коефіцієнт кореляції. Знайти оцінки параметрів лінійної регресії. Вибірка: Xi: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Yi: 13.3 12.2 12.4 12.4 16.4 22.0 17.2 21.8 22.4 24.8 21.3 26.7 17.9 19.5 30.1 26.7 31.0 28.4 20.0 24.7 26.9 21.3 28.6 27.7 30.0 22.9
2. На основі кореляційної матриці
необхідно визначити оцінку часткового коефіцієнта кореляції
3. На основі кореляційної матриці
необхідно визначити оцінку часткового коефіцієнта кореляції
4. На основі вибірки:
Xi: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Yi: 13.3 12.2 12.4 12.4 16.4 22.0 17.2 21.8 22.4 24.8 21.3 26.7 17.9 19.5 30.1 26.7 31.0 28.4 20.0 24.7 26.9 21.3 28.6 27.7 30.0 22.9
необхідно: побудувати кореляційне поле; обчислити коефіцієнт кореляції, перевірити його значущість; знайти оцінки параметрів лінійної регресії.
5. На основі вибірок: 1. Обчислити середнє та дисперсію двох виборок. 2. Перевірити головну гіпотезу за критерієм співпадання середніх з похибкою a=0.1. Вибірки: X: -0.8 0.8 0.6 0.3 -0.6 -3.0 1.8 0.2 1.3 2.4 1.0 1.2 1.2 0.8 -0.5 -1.9 -0.7 0.4 1.3 -2.2 0.5 2.7 1.2 0.8 -1.5 -0.2 -1.0 0.0 -0.5 -0.1 Y: -0.3 0.3 0.8 1.1 0.8 -0.1 -2.5 2.3 0.7 1.8 2.9 1.5 1.7 1.7 1.3 0.0 -1.4 -0.2 0.9 1.8 -1.7 1.0 3.2 1.7 1.3 -1.0 0.2 -0.5 0.4 0.0 0.3
6. Задано вибірку. Побудувати гістограму відносних частот, ідентифікувати модель розподілу, обчислити оцінки параметрів ідентифікованого розподілу. 0.55, 0.02, 0.77, 0.03, 0.55, 0.76, 0.48, 0.78, 0.82, 0.29, 0.54, 0.49, 0.01, 0.02, 0.92, 0.39, 0.29, 0.93, 0.11, 0.50, 0.30, 0.11, 0.10, 0.72, 0.79, 0.32, 0.95, 0.72, 0.96, 0.66, 0.15, 0.06, 0.09, 0.18, 0.40, 0.33.
7. Задано вибірку. Побудувати гістограму відносних частот, ідентифікувати модель розподілу, обчислити оцінки параметрів ідентифікованого розподілу. 7.85, 8.88, 11.73, 8.33, 12.47, 10.49, 9.10, 17.14, 8.68, 9.31, 9.50, 13.74, 8.89, 7.68, 9.08, 9.22, 10.23, 11.58, 9.14, 10.13, 12.20, 10.27, 10.75, 7.77, 7.02, 12.01, 7.93, 9.69, 10.64, 10.76, 12.05, 4.56, 13.37, 14.04, 10.58, 11.73, 10.42, 7.88, 10.11, 11.86, 7.80, 9.92, 9.69, 12.28, 12.01, 11.04, 6.92, 10.47, 10.34.
8. Задано дві одновимірни вибірки. Відомо:
9. Задано вибірку. Побудувати гістограму відносних частот, ідентифікувати модель розподілу, обчислити оцінки параметрів ідентифікованого розподілу. 1.94, 0.67, 0.41, 0.15, 0.01, 1.20, 1.16, 0.99, 0.80, 1.39, 0.31, 0.74, 0.85, 0.72, 0.83, 0.89, 1.85, 0.21, 0.12, 1.34, 0.15, 1.06, 0.11, 0.23, 1.91, 0.07, 0.62, 0.27, 1.66, 0.45, 2.06, 1.05, 0.75, 2.73, 1.30, 0.18.
10. Задано дві вибірки. Необхідно: а) побудувати кореляційне поле; б) обчислити коефіцієнт кореляції; б) перевірити значимість коефіцієнту кореляції, зробити висновок про наявність стохастичного зв’язку; в) відтворити лінійну регресію. xi – оцінка за тестами читання, yi – оцінка за тестами арифметики
|



 ,
, .
. ,
,


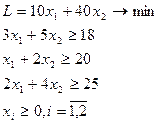

 .
.
 .
. ,
,  ,
,  ,
,  , вибірки незалежні,
, вибірки незалежні,  ,
,  . Перевірити однорідність.
. Перевірити однорідність.