 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Знайти загальний розв’язок диференціального рівняння
10. Знайти загальний розв’язок диференціального рівняння:
Теорія ймовірностей 1. Робітник обслуговує шість верстатів-автоматів. Ймовірність того, що протягом години верстат-автомат потребує уваги робітника є величиною сталою і дорівнює 0,6. Яка ймовірність того, що за годину уваги робітника потребують:1)три верстати; 2) від двох до п’яти верстатів; 3)принаймі один. 2. Ймовірність того, що студент складе іспит з математики дорівнює 0,8. Нехай є група з 8 студентів. Знайти найімовірнішу кількість членів цієї групи котрі складуть іспит з математики і обчислити відповідну ймовірність. 3. Ймовірність виходу з ладу під час проведення експерименту, який має на меті виявити надійність виробу в роботі, дорівнює 0,2. Було перевірено 400 виробів. Чому дорівнює ймовірність такої події: абсолютна величина відхилення відносної частоти виходу з ладу виробів від ймовірності p=0,2 становить 0.01? 4. Ймовірність появи випадкової події в кожному з 900 незалежних експериментів є величиною сталою і дорівнює 0,75. Яким має бути значення ε >0, щоб P(|W(A)-p|< ε)=0,99? 5. Автомобілі, що рухаються по шосе в одному напрямку, утворюють найпростіший потік із параметром λ=3с-1 (тобто через умовну лінію проїжджає 3 авто за 1 сек.). Обчислити ймовірність того, що за 2 сек. Через умовну лінію проїде :1)4 авто; 2)не більше як 4. 6. Троє складають іспит з теорії ймовірностей. Ймовірність того, що перший студент складе іспит становить 0,9, для другого та третього студентів ця ймовірність дорівнює відповідно 0,85 і 0,8. Побудувати закон розподілу ймовірностей ДВВ Х – числа студентів, які складуть іспит. Побудувати функцію розподілу. 7. Ймовірність того, що футболіст реалізує одинадцятиметровий штрафний удар дорівнює 0,9. Футболіст виконав три удари. Побудувати закон розподілу ймовірностей ДВВ Х – числа реалізованих штрафних. Побудувати функцію розподілу. Знайти числові характеристики ДВВ Х. 8. П’ять приладів випробують на надійність. Ймовірність того,що окремо взятий прилад витримає режим випробування , дорівнює 0,85. Нехай Х – число приладів,які витримають випробування, а Y – число приладів, які не витримають їх. Побудувати закон спільного розподілу X і Y. Обчислити Кxy, rxy. 9. Монета підкидається доти, доки вона випаде гербом. Знайти М(Х), D(Х) ДВВ Х – числа здійснених підкидань. 10. Скільки необхідно провести експериментів, щоб ймовірність відхилення відносної частоти W(A) появи випадкової події від ймовірності Р=0,85, взяте за абсолютною величиною, на ε=0,001, була б не меншою за 0,99.
Випадкові процеси 1. Нехай
2. Для рівняння Іто
Побудувати вираз для стохастичного диференціалу Іто від функції
3. Знайти розв’язки стохастичних рівнянь Іто
4. Нехай
5. Чи існує перший інтеграл для стохастичного рівняння
де 6. Перейти від рівняння Іто
до стохастичного рівняння у формі Стратоновича. 7. Перейти від рівняння у формі Стратоновича
до рівняння Іто 8. Нехай
де Перевірити , чи є першим інтегралом рівнянь Іто:
де
|




 .
.
 ,
,  , де a, b – незалежні випадкові величини з однаковими дисперсіями
, де a, b – незалежні випадкові величини з однаковими дисперсіями  та математичними сподіваннями
та математичними сподіваннями 

 ,
, 



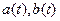 - скалярні функції.
- скалярні функції.
 - є скалярні функції
- є скалярні функції
 - скалярна функція.
- скалярна функція. - ?
- ?
 - векторний добуток,
- векторний добуток, 
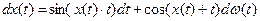
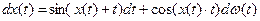

 - означає скалярний добуток.
- означає скалярний добуток.
 ,
, - одновимірний вінерівський процес.
- одновимірний вінерівський процес.