 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ОСОБЛИВІ ТОЧКИ БАГАТОКУТНИКІВ
І МНОЖИН N ТОЧОК ПЛОЩИНИ 3.1. Побудова кола, описаного навколо трикутника чи правильного n-кутника. Нехай трикутник або правильний n-кутник заданий координатами своїх вершин. Для розв’язання задачі нам достатньо знайти координати центру кола, тоді його радіус R виразимо через координати центру і координати будь-якої з його вершин. Зауважимо, що задача знаходження радіусу такого кола є простою для трикутника Р1Р2Р3 і спирається на співставлення двох формул для площі трикутника: З курсу геометрії відомо, що центр описаного кола лежить на перетині серединних перпендикулярів проведених до сторін трикутника. Координати середини сторони трикутника є середнім арифметичним координат відповідних векторів. Тоді задача знаходження рівняння серединного перпендикуляра співпадає з задачею 1.3 і за формулою (7) ми маємо: Для правильного багатокутника розв’язування нічим не відрізняється від наведеного вище. Достатньо записати рівняння двох будь-яких не співпадаючих серединних перпендикулярів, що не співпадають. Бо саме перетин всіх серединних перпендикулярів до сторін багатокутника в одній точці дозволяє описати коло навколо правильного n-кутника. Але є кращий спосіб. У випадку, якщо N – парне, центр правильного N-кутника – це середина проведеної діагоналі, наприклад з першої вершини в Зауважимо, що в правильному багатокутнику центр описаного кола співпадає з центром одиничних мас, розміщених в його вершинах. Тому його розташування також можна обчислити за формулою (15) див. 3.7 (далі). 3.2. Побудова кола вписаного в трикутник або правильний n-кутник. Як і в попередній задачі, радіус r такого кола для трикутника легко знайти із співвідношення формул обчислення площі трикутника: Центр вписаного в трикутник кола лежить на перетині бісектрис його кутів. Для знаходження його координат достатньо записати рівняння будь-яких двох бісектрис (див. задача 1.5) і знайти точку їх перетину. Центр кола, вписаного в правильний багатокутник, співпадає з центром описаного кола, а його радіус рівний відстані від центру до будь-якої із сторін. Як і з описаним колом, шуканий радіус можна обчислити відразу, не шукаючи центру, за формулою: 3.3. Коло, що «охоплює» N точок площини. Ця задача полягає у відшуканні координат центру кола мінімально можливого радіусу, всередині якого знаходяться всі задані точки. Інколи дану задачу називають мінімаксимальною задачею «про культурний центр». В цій задачі потрібно за координатами будівель міста підібрати місце для будівництва культурного центру так, щоб відстань до максимально віддаленого від нього будинку була мінімальною. Для того щоб зрозуміти розв’язок даної задачі в загальному випадку, розглянемо спочатку «трикутний» варіант: N=3. Навіть для трьох точок розв’язок залежить від їх взаємного розміщення. Нехай точки лежать на одній прямій або утворюють тупокутний трикутник. Тоді шукана точка лежить на середині відрізка, який з’єднує найбільш віддалені точки (на середині найбільшої сторони трикутника). Справді, відстань від цієї точки до будь-якої з перших двох зменшити неможливо, а третя точка знаходиться на меншій відстані від знайденої точки, тому вона лежить всередині кола, діаметр, якого утворює дві інші точки. А для гострокутного трикутника розв’язком буде центр описаного кола (зміщення шуканої точки в будь-якому напрямку призведе до збільшення відстані хоча б до однієї з точок). Спосіб його знаходження був показаний в задачі 3.1. Прямокутний трикутник є «граничним» для цих двох випадків, тобто для нього шукану точку можна шукати будь-яким із описаних способів (але перший спосіб є простішим). Для довільного N також є два випадки. Якщо знайдеться такі дві точки, що коло, побудоване на відрізку, який з’єднує ці точки, як на діаметрі, містить в собі всі інші точки (тобто для них виконується нерівність 3.4. Найбільше «порожнє» коло з центром всередині багатокутника, який містить N точок площини. Дану задачу можна сформулювати, як задачу «про хімічний завод». А саме, в межах міста, границя якого відома, а будинки задані своїми координатами, потрібно вибрати місце для будівництва хімічного заводу так, щоб відстань від нього до найближчого будинку була максимальною. Фактично нам потрібно знайти коло з максимальним радіусом, яке не має всередині точок з початкової множини, центр якого лежить всередині або на границі заданої ламаної. Тут можливі три випадки розміщення центру шуканого кола. Спочатку припустимо, що він лежить всередині ламаної. Тоді коло проходить обов’язково через три точки заданої множини, інакше, знайдеться «порожнє» коло і більшого радіусу. Тому переберемо всі не колінеарні трійки точок і для кожної трійки розглянемо коло, яке через них проходить. З цих кіл виберемо ті, центр яких лежить всередині ламаної і не містить в собі інших точок. Знайдемо серед них коло з найбільшим радіусом (позначимо його r1). У другому випадку центр шуканого кола лежить на ламаній, але не співпадає з її вершинами. Шукане коло тут визначається вже парою точок. Центри таких кіл лежать на перетині ламаної із серединним перпендикуляром до відрізка, який з’єднує дві точки (мал. 13). Позначимо максимальний радіус «порожніх» кіл даного виду r2. Тепер, якщо центр шуканого кола співпадає з однією із вершин ламаної, то його радіус буде визначатись відстанню найближчої до вершини точки (максимальний з даних радіусів позначимо r3). Відповіддю до нашої задачі буде радіус одного з трьох знайдених кіл, який є max(r1,r2,r3). Пошук розв’язку можна здійснити за O(NlogN) операцій.
Мал. 13 Наш алгоритм має допустиму обчислювальну складність, але при його реалізації доводиться використовувати відразу декілька елементарних задач, розглянутих вище. Як правило, для школярів повне розв’язання є дуже складним. Тому цього покажемо наближений метод розв’язку даної задачі, трохи спростивши її. Припустимо, що ламана являє собою прямокутник, лівий нижній кут якого розташований в початку координат, координати правого верхнього (xr,yr) відповідають довжині і ширині прямокутника. Це спрощення не зменшує загальності, оскільки навколо кожного багатокутника можна описати прямокутник і розв’язати дану задачу для цього прямокутника. Центри кіл, які лежать за межами багатокутника, розглядати не потрібно. Нехай ми хочемо знайти «порожнє» коло радіуса r. Тоді, щоб перевірити, чи ми зможемо це зробити, виконаємо наступну операцію: побудуємо кола радіуса r з центром в кожній з точок. Якщо ці кола покривають прямокутник повністю, то очевидно, що «порожнього» кола вказаного радіуса не існує. Будь-яка не покрита такими колами точка прямокутника може бути центром «порожнього» кола. Даний метод в геометрії називається методом «роздуття». Ми звели початкову задачу до іншої: задачі про покриття. 3.5. Задача про покриття. Припустимо, ми хочемо перевірити, що деякий прямокутник повністю покривається заданою множиною кіл. Якщо всі чотири його вершини покриваються одним колом, то прямокутник покривається колами повністю. В противному випадку розіб’ємо прямокутник на чотири однакових прямокутники і рекурсивно перевіримо, що кожний з них покривається колами. Для цього прямокутники, які не містяться повністю всередині якого-небудь одного кола, знову будемо ділити на чотири частини. Виключенням буде випадок, при якому вершина розглянутого прямокутника буде поза межами всіх кіл, тобто буде прикладом не покритої точки. Будемо продовжувати розбиття, поки сторона прямокутника не стане меншою за деяку задану достатньо малу величину. Тоді припустимо, що даний прямокутник повністю колами не покривається колом, а його центр будемо вважати не покритою точкою. Рекурсивна функція Check, що виконує відповідну перевірку, наведена нижче: Const еps1=1e-6; {точність пошуку непокритої точки} еps2=1e-5; {точність пошуку радіуса} var fx, fy: real; {координати цетру кола} xr, yr: real; {розміри прямокутника} lb, rb,r: real; {r – шуканий радіус} function dist2(x1, y1, x2, y2: real): real; {обчислює квадрат відстані між двома точками} Begin dist2:=sqr(x1-x2)+sqr(y1-y2) end; function check(x1, y1, x2, y2: real): boolean; {перевіряє, чи прямокутник покривається заданою множиною кругів; параметри – координати лівого верхнього і правого нижнього кутів прямокутника} var i: longint; d1, d2, d3, d4, c1, c2, c3, c4: boolean; Begin if (abs(x1-x2)<eps1 and (abs(y1-y2)<eps1 then begin{центр прямокутника – непокрита точка} fx:=(x1+x2)/2; fy:=(y1+y2)/2; check:=false; exit end; check:=true; c1:= true; c2:= true; c3:= true; c4:= true; {перевіряємо покриття одним кругом} for i:=1 to n do Begin d1:=dist2(x1, y1,x[i], y[i])<=r*r); d2:=dist2(x1, y2,x[i], y[i])<=r*r); d3:=dist2(x2, y1,x[i], y[i])<=r*r); d4:=dist2(x2, y2,x[i], y[i])<=r*r); if d1 and d2 and d3 and d4 then Begin check:=true; exit end; c1:=c1 and not d1; c2:=c2 and not d2; c3:=c3 and not d3; c4:=c4 and not d4 end; if c1 then {точка x1, y1 не покрита} Begin fx:=x1; fy:=y1; check:=false; exit end; if c2 then {точка x1, y2 не покрита} Begin fx:=x1; fy:=y2; check:=false; exit end; if c3 then {точка x2, y1 не покрита} Begin fx:=x2; fy:=y1; check:=false; exit end; if c4 then {точка x2, y2 не покрита} Begin fx:=x2; fy:=y2; check:=false; exit end; check:=check(x1, y1, (x1+x2)/2, (y1+y2)/2) and check((x1+x2)/2, y1, x2, (y1+y2)/2) and check(x1, (y1+y2)/2, (x1+x2)/2, y2) and check((x1+x2)/2, (y1+y2)/2, x2, y2) end; Тепер ми легко можемо розв’язати і задачу про «порожнє» коло максимального радіуса. За допомогою функції Check шуканий радіус кола також можна знайти алгоритмом ділення пополам: lb:=0; {ліва межа} if xr<yr then rb:=xr/2 else rb:=yr/2; {права межа} while abs(lb-rb)>eps2 do Begin r:=(lb+rb)/2; if check(r, 0,0, xr, yr) then rb:=m else lb:=m end; writeln (fx:0:4, ’’, fy:0:4, ’’, r:0:4); Таким не складним способом можна розв’язати задачу з будь-якою точністю. 3.6. Найкоротша мережа доріг. Задані N населених пунктів (точок на площині). Необхідно прокласти між ними дороги так, щоб по цих дорогам можна проїхати з будь-якого пункту в будь-який інший, а сумарна довжина доріг була мінімальною. На відміну від подібної задачі побудови мінімального остова в теорії графів в даній задачі ми не обмежені відрізками прямих, які з’єднують задані точки. При необхідності ми можемо побудувати в довільних місцях площини нові точки перетину частин доріг (так, для чотирьох точок, розташованих у вершинах квадрата, система доріг, побудована з двох діагоналей цього квадрату, краща за любе основне дерево, але і вона не являється оптимальною, див. на мал. 14 розв’язання для прямокутника.
Мал. 14 Розглянемо розв’язання задачі для N=3 (населені пункти лежать у вершинах трикутника АВС). Неважко зрозуміти, що в цьому випадку задача зводиться до пошуку точки, сума відстаней від якої до всіх вершин трикутника мінімальна, і така точка повинна лежати всередині або на стороні трикутника АВС. Припустимо, що кожний з кутів трикутника АВС не більший за 120о. Нехай D – довільна точка. Розглянемо трикутник
Мал. 15 З проведеного аналізу слідує і спосіб побудови точки Штейнера (мал. 16). Спочатку шукаємо точки
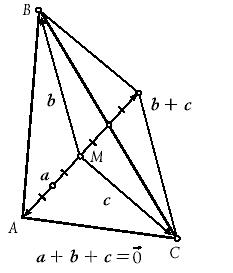
 Мал. 16 Для трикутників, у яких один з кутів більше 120о (в тому числі виродженого у відрізок), запропонована нами побудова не підходить. Дійсно, в такому трикутнику не має точки з якої всі три сторони було б видно під кутом 120о. В даному випадку розв’язком задачі буде система з двох найменших сторін трикутника. На мал. 14 показано розв’язок нашої задачі для чотирьох точок, розміщених у вершинах прямокутника. Для довільних N точок задача про найкоротшу мережу доріг не розв’язана. Тому пошук мінімальної транспортної мережі здійснюється з використанням комп’ютера. Але всі відомі на сьогодні алгоритми дозволяють побудувати розв’язок лише при невеликих значеннях N. 3.7. Центр мас. В деяких задачах геометрії корисно використовувати центр мас. Нехай на площині є система матеріальних точок А1,А2,…,АN, які мають відповідні маси m1,m2,…,mN. Будемо рахувати, що маси – не від’ємні числа (деколи допускаються від’ємні і навіть комплексні маси). Центром мас такої системи матеріальних точок називається точка М, для якої
Простий випадок: точка перетину медіан в трикутнику є центром трьох рівних мас, розміщених у вершинах даного трикутника. Це випливає з теореми про медіани (мал. 17)
Мал. 17 Повернемся до N точок. Нехай О – довільна точка площини. Використовуючи визначення точки М, отримаємо:
В якості точки О можна взяти початок координат. Тоді знайдемо координати точки М:
– де (xi, yi) – координати Аі. Застосування центру мас основується на його означенні (14). Покажемо це на одному з прикладів. Задача «мережа» Губернатор однієї з областей заключив договір з фірмою «GopNet» контракт на підключення всіх міст області до комп’ютерної мережі. Мережа створюється наступним чином: в області встановлюється станція супутникового зв’язку, а після чого з кожного міста прокладається кабель до станції. Технологія, яка використовується компанією, для виключення накопичення помилок вимагає при збільшенні відстані збільшення товщини кабелю. Ціна кабелю, який поєднує міста з станцією, при використанні компанією даної технології дорівнює kL2, де L – відстань від міста до станції, а k - деякий коефіцієнт. Потрібно визначити розміщення станції, при якому затрати компанії на побудову мережі будуть мінімальні. Розмістимо в кожне місто масу k, і нехай М – центр мас отриманої системи рівних точкових мас. Якщо станцію встановити в точці Р, то вартість S всього кабелю обчислюється таким чином:
Звичайно величина S мінімальна, коли БАГАТОКУТНИКИ 4.1. Визначення виду трикутника. Спочатку розглянемо, як для трьох дійсних чисел a, b і с перевірити, чи існує трикутник з довжинами сторін, які відповідають заданим числам. Відомо для додатних a, b і с повинні виконуватись умови існування трикутника а+b>c, a+c>b і b+c>a. Перевірки цих нерівностей достатньо у будь-якому випадку. Дійсно, додавши перші дві нерівності, отримаємо 2a+b+c>b+c, звідси а>0. З інших пар нерівностей випливає b>0 і c>0. Звідси, перевірку знаку a, b і с виконувати не потрібно. Якщо трикутник заданий координатами своїх вершин, то обчислювати довжини сторін і перевіряти існування трикутника не потрібно. В цьому випадку трикутник не існує тільки тоді, коли дані точки лежать на одній прямій. Це можна перевірити, обчисливши значення косого добутку Як вияснити за координатами вершин трикутника, чи гострокутний він, чи прямокутний або чи тупокутний? Для цього достатньо знати, яким є найбільший його кут. Вид кута легко визначити за знаком скалярного добутку утворюючих його векторів: більше нуля для гострого кута, рівне нулю для прямого і менше нуля для тупого. Тому підрахуємо всі три скалярних добутки, перемножимо їх і за знаком добутку визначимо вид трикутника. Зверніть увагу, що значення самих кутів обчислювати не потрібно. 4.2. Перевірка опуклості багатокутника. Опуклість багатокутника з вершинами Р1,Р2,…,Рn, перерахованих в порядку його обходу, легко перевірити, якщо визначити знаки косих добутків 4.3. Обчислення площі простого багатокутника. Під простим багатокутником ми розуміємо такий багатокутник, границя якого не має самоперетинів і самодотикань. Нехай вершини Р1,Р2,…,Рn простого багатокутника перераховані за порядком обходу його границі. Нагадаємо, що для обчислення його орієнтованої площі потрібно додати орієнтовані площі трикутників ОР1Р2, ОР2Р3,…, ОРnР1, де О – довільна точка площини. Модуль отриманої величини і є шукана площа:
– де вважається Рn+1=Р1. В якості точки О в деяких задачах буває доцільно вибрати одну з вершин багатокутника. Якщо ж за точку О взяти початок координат, то формула (16) набуде іншого вигляду, також зручного для програмування:
– де (хі, уі) – координати точки Рі. 4.4. Побудова опуклої оболонки для множини з N точок площини. Опуклою оболонкою деякої заданої множини точок називається перетин всіх опуклих множин, що містять задану множину. Для скінченої множини точок опуклою оболонкою буде завжди опуклий багатокутник, всі вершини якого є точками заданої множини.
Мал. 18 Перерахунок точок шуканої межі опуклого багатокутника почнемо з правої нижньої точки Р1, яка належить межі опуклої оболонки. Позначимо її координати (х1, у1). Наступною при заданому обході буде точка Р2(х2, у2). Вона має таку властивість, яку мають всі інші точки , що лежать зліва від вектора Аналогічно будемо шукати інші вершини. Припустимо, що вже знайдена і-та вершина Рі(хі, уі) опуклої оболонки. Для наступної точки Рі+1(хі+1, уі+1) косі добутки [ При розв’язуванні даної задачі у випадку цілочисельних координат ми повністю можемо уникнути використання дійсної арифметики, а тому, уникнути від втрати точності обчислень. В противному випадку в розв’язках можуть бути отримані «лишні» точки, близькі до межі опуклої оболонки , або не враховані деякі з «потрібних» точок. Складність даного алгоритму О(kN), де k – кількість точок опуклої оболонки, в гіршому випадку дорівнює N. Наведемо варіант реалізації даного алгоритму. Множина даних точок знаходиться в масиві, а всі точки, що належать опуклій оболонці, будемо записувати в масив b. type vv=record x, y: longint; end; var a, b: array [1..100] of vv; min, m, i, j, k, n: integer; function vect (a1, a2, b1,b2: vv): longint; {косий добуток векторів a1a2 і b1b2} Begin vect:=(a2.x-a1.x)*(b2.y-b1.y)-(b2.x-b1.x)*(a2.y-a1.y) end; function dist2(a1, a2: vv): longint; {квадрат довжини вектора a1a2} Begin dist2:=sqr(a2.x-a1.x)+sqr(a2.y-a1.y) end; begin {Main} readln (n); {кількість точок} for i:=1 to n do read (a[i].x, a[i].y); {шукаємо праву нижню точку} m:=1; for i:=2 to n do if a[i].y<a[m].y then m:=i else if (a[i].y=a[m].y) and (a[i].y>a[m].y) then m:=i; {запишемо її в масив опуклої оболонки b і переставимо на перше місце в масиві a} b[1]:=a[m]; a[m]:=a[1]; a[1]:=b[1]; k:=1; min:=2; Repeat {шукаємо наступну вершину опуклої оболонки} for j:=2 to n do if (vect(b[k], a[min], b[k],a[j])<0 or ((vect(b[k], a[min], b[k],a[j])=0) and (dist2(b[k], a[min])< (dist2(b[k], a[j]))) then min:=j; k:=k+1; {записана наступна вершина} b[k]:=a[min]; min:=1; until (b[k].x=b[1].x) and (b[k].y=b[1].y); {поки ламана не замкнеться} for j:=1 to k-1 do {друк результатів} writeln (b[j].x,’’,b[j].y) end. Існує інший алгоритм розв’язання цієї задачі (алгоритм Грехема) з обчислювальною складністю О(NlogN), оснований на попередньому сортуванні точок даної множини за значенням кута в полярній системі координат з центром в одній із точок опуклої оболонки. Тобто найбільш складним буде сортування заданих точок. Сортування точок можна виконувати за знаком косого добутку [
Мал.19. Вершини опуклої оболонки множини точок {Pi}: P1, P4, P5, P6, P9, P12. Номери всіх точок відповідають сортуванню за полярним кутом.
Далі перегляд Грехема використовує стек, в якому зберігаються точки, що є претендентами в опуклу оболонку. Спочатку в стек заносять першу з відсортованих точок. Потім – сусідню з нею вершину опуклої оболонки. Якщо на першому із променів точок декілька, то ця точка променя Pi, найбільш віддалена від P1. Третя – точка Pі+1. Нехай на вершині стека знаходиться точка Pk. Розглянемо наступну в порядку збільшення полярного кута точку заданої множини Pi. Поки частина ламаної Pk-1, Pk, Pi не є опуклим (див. задачу 4.2.), із стеку вилучається наступна точка Pk. Потім Pi заноситься до стеку. В момент закінчення перегляду всіх точок в стеці будуть знаходитись всі вершини опуклої оболонки. Так як будь-яка точка заноситься в стек не більше одного разу, тому час перегляду складає О(N). Наведемо приклад реалізації саме цього перегляду. Для наочності сортування зробимо методом «бульбашки». В якості стека використовується масив b. Описи змінних і функцій співпадають з наведеними вище. Begin readln (n); fori:=1tondo read(a[i].x, a[i],y); {шукаємо праву нижню точку} m:=1; for i:=2 to n do if a[i].y< a[m].y then m:=i else if (a[i].y= a[m].y) and (a[i].x> a[m].x) then m:=i; {запишемо її в масив опуклої оболонки b і переставимо на перше місце в масиві а } b[1]:=a[m]; a[m]:=a[1]; a[1]:=b[1]; {інші точки сортуємо методом «бульбашки» за значенням полярного кута} for i:=n downto 3 do for j:=2 to i-1 do if (vect (a[1], a[j], a[1], a[j+1])<0 or ((vect (a[1], a[j], a[1], a[j+1])=0) and (dist2(a[1],a[j]>dist2(a[1], a[j+1]))) Then begin {b[n]-допоміжна змінна} b[n]:=a[j]; a[j]:=a[j+1]; a[j+1]:=b[n] end; {шукаємо другу вершину опуклої оболонки} i:=2; while vect(a[1], a[i+1], a[1], a[2])=0 do i:=i+1; b[2]:=a[i]; b[3]:=a[i+1]; k:=3; for i:=i+2 to n do begin while vect(b[k-1], b[k], b[k], a[i])<=0 do k:=k-1; {видаляємо точку з стека } k:=k+1; b[k]:=a[i] {додаємо точку в стек} end; forj:=1 to k do {друк розв’язку} writeln (b[j].x,’’,b[j].y) End. На цьому ми закінчуємо огляд розв’язувань елементарних задач обчислювальної геометрії на площині. Їх можна використовувати при розв’язуванні більш складних, наприклад олімпіадних задач.
ЗАДАЧІ Задача 1. На площині задані дві точки A(x1,y1) і B(x2,y2). Визначити, який з відрізків - OA чи OB утворить більший кут з віссю OX. Задача 2. Чи належить точка площини А відрізку з кінцями B і C? Задача 3. 1. Опуклий багатокутник задається координатами вершин при його обході за чи проти годинникової стрілки. Контур багатокутника не має самоперетинань. Визначити напрямок обходу. 2. Виконати те саме, але тільки у випадку не опуклого багатокутника. Задача 4. Відрізок на площині задається двома не співпадаючими точками X(x1,x2) і Y(y1,y2). З точки Z(z1,z2) до прямої, що містить відрізок [X,Y], проводиться перпендикуляр P. Визначити, чи попадає перпендикуляр P на відрізок [X,Y] чи на його продовження. Задача 5. Багатокутник на площині задається координатами своїх N вершин у порядку обходу їх по контурі за годинниковою стрілкою. Вважається, що контур самоперетинань не має. Знайти площу, периметр і кути багатокутника. Задача 6. Визначити, чи перетинаються пряма ax+b=y і відрізок з кінцями (x1,y1), (x2,y2). Задача 7. Два відрізки на площині задаються парами цілочисельних координат кінців. Визначити, чи перетинаються відрізки. Задача 8. 1. Трикутник на площині задається цілочисельними координатами вершин. Для заданої точки Z(x,y) визначити, чи належить вона стороні трикутника чи лежить усередині чи поза ним. 2. Багатокутник на площині задається координатами своїх N вершин у порядку обходу їх по контурі за годинниковою стрілкою (контур самоперетинань не має). Для заданої точки Z(x,y) визначити, чи належить вона стороні багатокутника чи лежить всередині чи поза ним. Задача 9. На площині задані n відрізків координатами кінців. Кінці відрізків задаються двома парами координат (x1[і],y1[і]), (x2[і],y2[і]), 1<=і<=n (кінці належать відрізку). Необхідно знайти пряму, що має спільні точки з максимальним числом відрізків, і надрукувати в порядку зростання номери тих відрізків, які ця пряма перетинає. Задача 10. N точок на площині задані своїми координатами. Знайти такий мінімальний по площі опуклий багатокутник, що всі N точок лежать або всередині цього багатокутника, або на його границі (такий опуклий багатокутник називається опуклою оболонкою). Задача 11. На сітці розміру m*n задано k точок своїми координатами. Необхідно визначити, чи можна побудувати опуклий багатокутник такий, що кожна точка належить деякій стороні. Задача 12. N точок на площині задані своїми координатами. Знайти порядок, у якому можна з'єднати ці точки, щоб вийшов N-кутник (тобто не було б перетинань сторін).
Задача 13. Уявіть собі, що в зошиті Ви замалювали на аркуші деяку кількість клітинок і отримали клітинну фігуру. Скільки осей симетрії має задана клітинна фігура. Пояснення : 1) Задається S - число тестів. Для кожного тесту задаються NІ розмір фігури по вертикалі, NJ - розмір фігури по горизонталі (NІ<101, NJ<81) і сама фігура у вигляді NІ рядків із пробілів і одиниць по NJ символів у кожному рядку. 2) Числа S, NІ, NJ займають при введенні по три позиції. Приклад . Вхідні дані : 2 ( кількість тестів ) 2 ( розмір 1-ої фігури по вертикалі ) 4 ( розмір 1-ої фігури по горизонталі ) 1 1 3 ( розмір 2-ий фігури по вертикалі ) 5 ( розмір 2-ий фігури по горизонталі ) Вихідні повідомлення: 1-А ФІГУРА МАЄ 1 ОСІ СИМЕТРІЇ 2-А ФІГУРА МАЄ 0 ОСІ СИМЕТРІЇ Задача 14. Прямокутник ABCD заданий координатами своїх вершин. На протилежних сторонах AB і CD задані послідовності R1 і R2 з N точок розбиття, а на сторонах BC і AD - R3 і R4 з M точок розбиття. Нумерація елементів послідовності R1 і R2 починається відповідно від точок A і D, а в R3 і R4 – від B і A. З'єднавши відрізками точки з однаковими номерами в розбиттях R1 і R2, а потім у розбиттях R3 і R4, отримаємо розбиття Q прямокутника ABCD на множину чотирикутників. Побудувати алгоритм, що визначає чотирикутник розбиття Q з найбільшою площею, за умови, що відрізки, що з'єднують точки розбиття R1 і R2 паралельні стороні AD. Послідовності R1, R2, R3 і R4 задаються як масиви з довжин відрізків розбиття відповідних сторін прямокутника. Задача 15. На прямій задано N точок з координатами X1,X2,...,Xn. Написати програму, що знаходить на прямій таку точку Z, сума відстаней від якої до даних N точок мінімальна. Задача 16. На двовимірній площині задано N точок з координатами (X1,Y1), (X2,Y2), ..., (Xn,Yn). Написати програму, що знаходить таку точку Z(x,y), сума відстаней від якої до інших мінімальна і: а) Z - одна з заданих точок; b) Z - довільна точка площини. Задача 17. На площині розташовані N точок, задані своїми координатами. Знайти на осі абсцис точку, найбільша з відстаней від якої до обраних точок була б мінімальною. Задача 18. На площині задано N точок з координатами (X1,Y1), (X2,Y2), ..., (Xn,Yn). Написати програму, яка з цих точок виділяє вершини квадрата, що містить максимальне число заданих точок. ПРИМІТКА: передбачається, що точки, розташовані на сторонах квадрата, належать йому. Задача 19. Задано на площині множину з N прямокутників, сторони яких паралельні осям координат, при цьому кожен прямокутник задається координатами лівої нижньої і правої верхньої його вершин. Скласти алгоритм визначення найбільшого натурального числа К, для якого існує точка площини, що належить одночасно К прямокутникам. Примітка: ефективним вважається алгоритм, число дій якого пропорційно N2. Задача 20. На квадратному торті N свічок. Чи можна одним прямолінійним розрізом розділити його на дві рівні за площею частини, одна з яких не містила б ні однієї свічки? Свічки будемо вважати точками, у яких відомі їхній цілочисельні координати Х[1], Y[1]; ...; Х[N], Y[N] (початок координат - у центрі торта); розріз не може проходити через свічку. Задача 21. Дано N прямокутників (N>1), для яких передбачається, що: А) Сторони будь-якого прямокутника паралельні координатним осям і прямокутник задається кінцями однієї з діагоналей. В) Кожен прямокутник має спільні внутрішні точки хоча б з одним іншим прямокутником і не має спільних вершин, сторін чи частин сторін з жодним з інших прямокутників. Скласти програму, що розв’язує наступні задачі: 1. За допомогою послідовності точок визначити зовнішній контур фігури F, що є об'єднанням прямокутників в замкнуту ламану. Приклад на малюнку. 2. Визначити чи містить фігура F "дірки" ,тобто замкнуті фігури, що їй не належать. 3. Розкласти фігуру на найменше можливе число не пересічних прямокутників, які не перетинаються, що можуть мати спільні сторони чи частини сторін , а їхнє об'єднання дає фігуру F. 4. Обчислити периметр і площу фігури F. Примітка. 1. Задачі 3,4 розв’язується тільки для фігур, що не містять "дірки". 2. Повне розв’язання містить: - аналіз (обґрунтування) розв’язку - текст програми з відповідними коментарями - виконання текстового прикладу, що буде за даний при прийманні роботи Об'єднання прямокутників Aі Bі Cі Dі,і=1,2,3,4 є фігура F=A2 B2 X1 B1 X2 B4 C4 D4 X3 X4 C2 D2 фігура F містить єдину "дірку" PQRS
Задача 22. Контур міста. Необхідно написати програму - помічник архітектора в кресленні контуру міста. Місто задається розташуванням будинків. Місто розглядається як двовимірне і всі будинки в ньому - прямокутники, що мають однакову основу (місто побудоване на рівнині). Будинки задаються трійкою чисел (L[і],H[і],R[і]) де L[і] і R[і] є координати лівої і правої стін будинку і, а H[і] - висота цього будинку. На малюнку 1 будинки описуються трійками (1,11,5), (2,6,7), (3,13,9), (12,7,16), (14,3,25), (19,18,22), (23,13,29),(24,4,28) а контур, показаний на мал. 2, задається послідовністю (1,11,3,13,9,0,12,7,16,3,19,18,22,3,23,13,29,0) (про спосіб формування цієї послідовності див. нижче).
Мал. 1
Мал. 2 Введення. Введення являє собою послідовність трійок, що задають будинки. Усі координати є цілі числа, менші 10000. В вхідному файлі мінімум один і максимум 50 будинків. Кожна трійка, що позначає будинок знаходиться в окремому рядку у вхідному файлі. Усі цілі числа в трійці розділені одним чи декількома пробілами. Трійки відсортовані по L[і], тобто по лівій х-координаті будинку, таким чином, будинок із самою мінімальною лівою х-координатою є першим у вхідному файлі. Висновок. Висновок буде складатися з вектора, що описує контур, як показано в прикладі вище. У векторі контуру (v[1],v[2],v[3], ... , v[n-2],v[n-1],v[n]), v[і], коли і-парне число, означає горизонтальну лінію (висоту). Коли і-непарне, v[і]- означає вертикальну лінію (х-координату). Вектор контуру буде визначати маршрут, пройдений, наприклад, жуком, що почав з мінімальної х-координаты і подорожує по усіх вертикальних і горизонтальних лініях, що визначає контур. Останній елемент у векторі лінії контуру буде 0. Задача 23. Нижня ліва і верхня права вершини прямокутника A відповідно мають координати (0,0) і (V,W). Множина S з N точок задається парами координат (x[і],y[і]), 1<=і<=N. Знайти такий прямокутник G максимальної площі, що його сторони паралельні сторонам A, G цілком лежить у A (G і A можуть мати спільні граничні точки) і жодна точка з S не лежить усередині G (але може лежати на його стороні). Надрукувати значення площі G і координати нижньої лівої і верхній правої вершин цього прямокутника. Якщо таких прямокутників декілька, то вивести інформацію по кожному. Примітка: у множині S жодні дві точки не лежать на одній прямій, паралельній стороні A. Необхідно: 1. Організувати введення даних у вигляді < Введіть V і W- координату верхньої правої вершини прямокутника A > < Введіть N - число точок > < Введіть координати точок > x[1]-> y[1]-і> ..... x[N]-> y[N]-і> 2. Вивести результати у вигляді < Максимальна площа прямокутника = > < Координати нижньої лівої і верхній правої вершин прямокутника(ов) > x1-> y1-> x2-> y2-> Задача 24. У першій чверті координатної системи OXY намальований перший квадрат - ABCD, довжина сторони якого дорівнює 1 і вершина A знаходиться на початку координат. Потім зображені: другий квадрат - BEFC, третій - DFGH, четвертий - JAHІ, п’ятий KLEJ, шостий - LMNG, і так далі «по спіралі» (мал.1). Написати програму, що для введених цілих чисел x і y визначає і виводить номер квадрата, якому належить точка P(x;y). Якщо точка P лежить на сторонах квадратів чи у вершинах, то будемо вважати, що вона належить квадрату з найменшим номером з можливих. Приклади:
Мал.1 Задача 25. На площині N різних точок, що задані своїми координатами. Знайти рівняння прямої, що поділяє цю множину точок на 2 рівноцінних підмножини (тобто на підмножини з однаковою кількістю елементів).
Задача 26. Знайти перетин й об'єднання двох опуклих багатокутників. Багатокутники задаються координатами вершин у порядку обходу по контурі. Задача 27. N-кутник на площині задається координатами вершин у порядку обходу по контурі (контур самоперетинів не має). Для точки Z(x,y) знайти мінімальну відстань до контуру N-кутника. Задача 28. На площині задано N точок своїми координатами і матриця C(N*N); C(і,j)=C(j,і)=1 у випадку, якщо вершини і і j з'єднані відрізком, інакше – 0. Відомо, що будь-яка вершина з'єднана принаймні з двома іншими, і що відрізки перетинаються тільки в кінцевих точках. Таким чином, вся площина розбивається на множину багатокутників. Задано точку Z(x,y). Знайти мінімальний за площею багатокутник, що містить Z, чи видати повідомлення, що такого не існує. Якщо Z належить деякому відрізку, то видати його кінці, якщо Z лежить у багатокутнику, то видати його вершини в порядку обходу по контурі. Задача 29. Будемо називати два багатокутники подібними, якщо існує взаємо-однозначне відображення сторін цих двох фігур таке, що відповідні сторони пропорційні з коефіцієнтом пропорційності k, а кути, утворені двома відповідними сторонами, рівні. Визначити, чи подібні два багатокутники. Багатокутники задаються на площині координатами вершин контурів. Вершини в контурі перелічуються в порядку обходу проти годинникової стрілки. Примітка: тому що всі обчислення на ЕОМ проводяться з обмеженою точністю, то вважати, що дві величини рівні якщо вони співпадають з точністю до двох знаків після коми. ВВЕДЕННЯ: <з файлу T.TXT> <Кількість вершин > N <Багатокутник 1:> <Координати вершини 1:> x11, y11 ..... <Координати вершини N:> x1N, y1N <Багатокутник 2:> <Координати вершини 1:> x21, y21 ..... <Координати вершини N:> x2N, y2N ВИСНОВОК: <Багатокутники не подібні> чи <Багатокутники подібні з k=> k Задача 30. Задано натуральне число N і дві послідовності цілих чисел (а1,а2,...,аn) і (b1,b2,...,bn). Задані також два числа X0 і X1, X0<X1. 1. Знайти числа t(0), t(1), ..., t(p), p<=N, такі ,що X0=t(0)<t(1)<...<t(p)=X1 і вказати для кожного відрізка [t(j-1), t(j)], 1<=j<=p, таке число k, 1<=k<=N, що для всіх і, 1<=і<=N, і для всіх x з [t(j)-1,t(j)] справедлива нерівність аk*x+bk>=аі*x+bі. 2.Знайти числа s(0), s(1), ..., s(Q), такі, що X0=s(0)<s(1)<...<s(Q)=X1, і вказати для кожного відрізка [s(j-1),s(j)], 1<=j<=Q, таку перестановку (і1,і2,...,і) чисел 1,2,3,...,N, що для всіх X з [s(j-1),s(j)] справедливе нерівність aі1*x+bі1<=аі2*x+bі2<=...<=аі*x+bі і для всіх відрізків відповідні перестановки різні. Задача 31. На площині задана множина точок А и множина прямих В. Знайти дві такі різні точки з А, що пряма яка проходить через них паралельна найбільшій кількості прямих з В.
Задача 32. У правильному n-кутнику провели кілька діагоналей, причому жодні три не перетинаються в одній точці. На скількі частин діагоналі розбили n-кутник? Діагоналі задані номерами вершин n-кутника, які вони сполучають, всі вершини пронумеровані по порядку числами 1, ...,n. Задача 33. Серед трикутників з вершинами в заданій множини точок на площині вказати такі, сторони якого містять максимальне число точок заданої множини. Задача 34. Усі стіни будинку мають довжину 5м. Північна та південна сторони – білі, західна і східні – сині. Людина пройшла від південно-східного кута будинку А метрів на південь, В метрів на схід і С метрів на північ і подивилася на будинок. Написати алгоритм, який визначає, що бачить людина. Задача 37. На місцевості, що представляє собою ідеально рівну поверхню, стоїть високий пліт. План плоту являє собою замкнуту ламану без самоперетинань. Ця ламана задається N парами координат своїх вершин у порядку обходу області, що обмежується плотом, проти годинникової стрілки. Вершини пронумеровані від 1 до N, N<100. У точці (x,y) стоїть людина ((x,y) не може лежати на ламаній). Вважаючи, що кожній ланці ламаної ставлять у відповідність пари номерів кінців, вказати, які ланки людина побачить повністю або частково в якості невирожденного відрізка, а яких - взагалі не побачить. Якщо при погляді ланку видно як точку чи як пару точок, то вважаємо, що іі не видно. Задача 37. На гранях двох рівних правильних тетраедрів N і M написані числа N1,N2,N3,N4 і M1,M2,M3,M4. Чи можна сумістити тетраедри так, щоб на співпадаючих гранях виявилися однакові числа?
Використані джерела 1. Кормен Т., Аейзерсон Ч., Риверст Р. Алгоритмы. Построение и анализ. М.: МЦНМО, 2000. 2. Шикин Е.В., Боресков А.В., Зайцев А.А. Начала компьютерной графики. М.: Диалог-МИФИ, 1993. 3. Курант Р., Роббинс Г. Что такое математика. М.: ОГИЗ, государственное издательство технико-теоретической литературы, 1947. 4. Окулов С.М. 100 задач по информатике. Киров: Издательство ВГПУ, 2000. 5. Станкевич А.С. Решение задач I Всероссийской командной олимпиады по программированию. Информатика №12/2001. 6. Андреева Е.В. Геометрические задачи на олимпиадах по информатике. Информатика №14/2002. 7. Караванова Т.П. Основи алгоритмізації та програмування 750 задач з рекомендаціями та прикладами. Київ «Форум», 2002. 8. http://www.algolist.manual.ru 9. http://www.g6prog.narod.ru 10. http://www.uoi.kiev.ua
|



 , нагадаємо, що перший спосіб випливає з геометричного змісту косого добутку.
, нагадаємо, що перший спосіб випливає з геометричного змісту косого добутку. , де (
, де ( 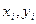 ) – координати точки
) – координати точки 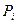 . Для знаходження центру шуканого кола достатньо записати ще один серединний перпендикуляр (наприклад, до відрізка Р1Р3) і знайти точку перетину цих двох прямих.
. Для знаходження центру шуканого кола достатньо записати ще один серединний перпендикуляр (наприклад, до відрізка Р1Р3) і знайти точку перетину цих двох прямих.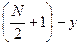 , тобто координати центра кола є середнім арифметичним координат зазначених вершин. Якщо N – непарне, то центр лежить на прямій, яка з’єднує одну із вершин з серединою найбільш віддаленої сторони, на відстані
, тобто координати центра кола є середнім арифметичним координат зазначених вершин. Якщо N – непарне, то центр лежить на прямій, яка з’єднує одну із вершин з серединою найбільш віддаленої сторони, на відстані  від вершини, де а – довжина сторони правильного n-кутника.
від вершини, де а – довжина сторони правильного n-кутника. .
.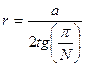 .
. , де
, де 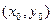 – центр кола), то це коло – шукане (фактично це є випадок «тупокутного трикутника»). Якщо ж такої пари точок не знайдеться, то шукане коло буде проходити хоча б через три точки. Тому тепер потрібно перебрати всі трійки точок до тих пір, поки не знайдеться така трійка, що проходячи через них, коло охопить всередині себе всі інші точки (випадок «гострокутного трикутника»).
– центр кола), то це коло – шукане (фактично це є випадок «тупокутного трикутника»). Якщо ж такої пари точок не знайдеться, то шукане коло буде проходити хоча б через три точки. Тому тепер потрібно перебрати всі трійки точок до тих пір, поки не знайдеться така трійка, що проходячи через них, коло охопить всередині себе всі інші точки (випадок «гострокутного трикутника»).

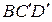 , отриманий поворотом трикутника
, отриманий поворотом трикутника  навколо т.
навколо т.  на 60о (мал. 15). За побудовою
на 60о (мал. 15). За побудовою 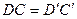 і
і  (трикутник
(трикутник  – рівносторонній). Тому шукана сума відстаней для т.
– рівносторонній). Тому шукана сума відстаней для т.  дорівнює
дорівнює  – і, отже, нам потрібно знайти таку т.
– і, отже, нам потрібно знайти таку т.  мінімальна. Якщо в якості т.
мінімальна. Якщо в якості т.  , див. на мал. 15 (
, див. на мал. 15 (  ), то після повороту навколо точки
), то після повороту навколо точки  . Таким чином, довжина
. Таким чином, довжина 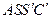 буде рівною
буде рівною  , і зрозуміло, не більша довжини любої другої ламаної
, і зрозуміло, не більша довжини любої другої ламаної  , так як промінь
, так як промінь  переходить в промінь
переходить в промінь  при повороті на 60о. Зрозуміло, що дві інші сторони трикутника повинно бути видно з точки
при повороті на 60о. Зрозуміло, що дві інші сторони трикутника повинно бути видно з точки 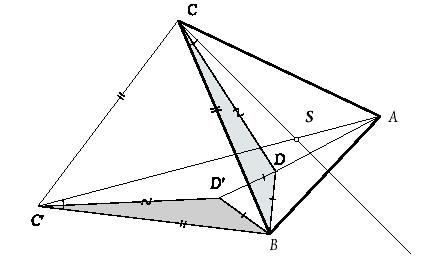
 і
і 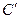 як вершини рівносторонніх трикутників
як вершини рівносторонніх трикутників  і
і  , побудованих за межами трикутника
, побудованих за межами трикутника  . Пошук їх координат здійснюється за допомогою вектора нормалі відкладеного до середини відповідної сторони трикутника (шукана точка знаходиться на відстані
. Пошук їх координат здійснюється за допомогою вектора нормалі відкладеного до середини відповідної сторони трикутника (шукана точка знаходиться на відстані  від середини сторони початкового трикутника, де а – довжина відповідної сторони). Залишається визначити т. S перетину відрізків
від середини сторони початкового трикутника, де а – довжина відповідної сторони). Залишається визначити т. S перетину відрізків  і
і 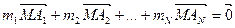 (14)
(14)

 (15)
(15)
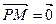 , тобто, коли станція знаходиться в центрі мас. Отже, координати шуканої точки шукаємо за формулою (15):
, тобто, коли станція знаходиться в центрі мас. Отже, координати шуканої точки шукаємо за формулою (15):  . Крім того, можна уявити, що по якійсь причині коефіцієнт k залежить від місцевості і є різним для кожного міста. Наш розв’язок легко адаптувати до цього випадку: треба розмістити в кожне місто масу, яка рівна відповідному коефіцієнту. Але знову ж станцію потрібно ставити в центрі мас отриманої системи матеріальних точок.
. Крім того, можна уявити, що по якійсь причині коефіцієнт k залежить від місцевості і є різним для кожного міста. Наш розв’язок легко адаптувати до цього випадку: треба розмістити в кожне місто масу, яка рівна відповідному коефіцієнту. Але знову ж станцію потрібно ставити в центрі мас отриманої системи матеріальних точок. . Якщо він рівний нулю, то відповідні вектори колінеарні, тобто всі три точки лежать на одній прямій.
. Якщо він рівний нулю, то відповідні вектори колінеарні, тобто всі три точки лежать на одній прямій. , i=1,..,n (тут Pn+1 є Р1, а Pn+2 – Р2). В опуклого багатокутника знаки всіх добутків або не додатні, або не від’ємні (тобто знаки ненульових добутків співпадають). Якщо ми знаємо напрямок обходу, то знак косих добутків для опуклого багатокутника визначений: при обході за годинниковою стрілкою всі косі добутки не додатні, а проти годинникової стрілки не від’ємні.
, i=1,..,n (тут Pn+1 є Р1, а Pn+2 – Р2). В опуклого багатокутника знаки всіх добутків або не додатні, або не від’ємні (тобто знаки ненульових добутків співпадають). Якщо ми знаємо напрямок обходу, то знак косих добутків для опуклого багатокутника визначений: при обході за годинниковою стрілкою всі косі добутки не додатні, а проти годинникової стрілки не від’ємні. (16)
(16) (17)
(17)
 , тобто орієнтований кут між векторами
, тобто орієнтований кут між векторами  невід’ємний для будь-якої іншої точки М нашої множини. Для претендента на роль точки Р2 перевіримо виконання умови [
невід’ємний для будь-якої іншої точки М нашої множини. Для претендента на роль точки Р2 перевіримо виконання умови [  ] невід’ємні для всіх точок М. Якщо таких точок декілька, то вибираємо ту, для якої вектор
] невід’ємні для всіх точок М. Якщо таких точок декілька, то вибираємо ту, для якої вектор  має найбільшу довжину. Пошук такої точки можна здійснювати так: спочатку ми можемо вважати наступною, (і+1)-шою, будь-яку точку. Потім знаходимо значення [
має найбільшу довжину. Пошук такої точки можна здійснювати так: спочатку ми можемо вважати наступною, (і+1)-шою, будь-яку точку. Потім знаходимо значення [  ], де Р1 – будь-яка вершина опуклої оболонки (наприклад, права нижня точка). У відсортованому масиві точок всі дані добутки повинні бути невід’ємними. Точки з рівними кутами ([
], де Р1 – будь-яка вершина опуклої оболонки (наприклад, права нижня точка). У відсортованому масиві точок всі дані добутки повинні бути невід’ємними. Точки з рівними кутами ([  (мал. 19).
(мал. 19).



