 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Рівняння прямої, яка проходить через дві різні точки, які задані своїми координатами.
ЗМІСТ
ПЕРЕДМОВА «Обчислювальна геометрія – це розділ інформатики, що вивчає алгоритми розв’язування геометричних задач. Такі задачі виникають в комп’ютерній графіці, в проектуванні інтегральних схем, технічних пристроїв та іншого. Вхідними даними в такого роду задачах може бути множина точок, набір відрізків, багатокутників і т.д. Результатом може бути відповідь на будь-яке запитання (типу «перетинаються дані прямі, чи ні»), або деякий геометричний об’єкт (наприклад, найменший опуклий багатокутник, який містить задані точки)». Заняття навіть з математично добре підготовленими учнями старших класів показали, що при розв’язанні геометричних задач в них виникають великі труднощі. Задачі заводять їх в глухий кут, або вибраний «прямий» спосіб розв’язування настільки складний, що довести його до логічного завершення без помилок, учні не можуть. Аналіз результатів розв’язування «геометричних» задач на олімпіадах з інформатики показує такі ж результати. Дану ситуацію можна виправити. Ціль цієї розробки – показати різні підходи до розв’язування геометричних задач на площині, які дозволять дуже швидко і максимально просто отримати розв’язки більшості елементарних підзадач.
Вектори і координати Щоб використовувати методи обчислювальної геометрії, необхідно геометричні зображення перевести на мову чисел. Будемо рахувати, що на площині задана декартова система координат (СК). Взагалі прийнято вибирати координатні осі так, щоб поворот на кут Тепер геометричні об’єкти отримають аналітичні вирази. Так, щоб задати відрізок, достатньо вказати координати його кінців. Пряму можна задати, вказавши дві її точки, або координати однієї її точки і вектор, який характеризує напрямок даної прямої. Взагалі при розв’язуванні задач основним інструментом для нас буде вектор. Нагадаємо для цього деякі відомості про нього. Відрізок АВ, в якому т. А вважається початком, а т. В – кінцем, називається вектором АВ, і позначається Нехай точки А і В мають координати (х1, у1) і (х2, у2) відповідно. Координатами вектора Вектори можна додавати і множити на скаляр. Сума векторів шукається за правилом трикутника, або за правилом паралелограма (мал. 1).
Мал. 1 Під різницею векторів а і b розуміють суму вектора а з вектором, протилежним вектору b (тобто протилежно направленим і співпадаючим з ним по довжині). При множені вектора а на скаляр t отримаємо вектор, який має довжину якщо а= то a+b=(ax+bx, ay+by), a-b=(ax-bx, ay-by) і t*a=(t*ax, t*ay). Скалярний добуток двох ненульових векторів а= В координатах це обчислюється таким чином: (a,b)=x1x2+y1y2. Як видно з формули, скалярний добуток можна використовувати для знаходження кута між векторами. Взагалі, два ненульових вектора перпендикулярні тоді і тільки тоді, коли їх скалярний добуток рівний нулю ( Кут між векторами Нехай а і b – два ненульових вектори, відкладені з однієї точки. В шкільній програмі з геометрії під кутом між векторами розуміють менший з двох кутів між променями, на яких лежать вектори а і b. Значення такого кута завжди знаходиться на проміжку Для обчислень найбільш зручнішим є поняття орієнтованого кута, тобто кута, що враховує взаємне розміщення векторів. Значення орієнтованого кута за абсолютною величиною рівне звичайному куту між векторами. Орієнтований кут між векторами а і b додатній, якщо поворот від вектора а до вектора b, здійснюється в додатному напрямку (в нашій СК проти годинникової стрілки), і від’ємний в протилежному випадку. Таким чином, величина орієнтованого кута залежить від порядку перерахунку векторів і може набувати значення на інтервалі
Мал. 2 Як, знаючи координати векторів, знайти кут між ними. Звичайно, з формули скалярного добутку: Орієнтована площа Орієнтована площа трикутника – це його звичайна площа наділена знаком. Знак в орієнтованій площі трикутника АВС такий ж, як і в орієнтованого кута між векторами Так само для обчислення площі будь-якого багатокутника А1А2…Аn потрібно додати площі трикутників ОА1А2, ОА2А3, …, ОАnА1 (мал. 3). В сумі отримаємо площу багатокутника, взяту із знаком плюс, якщо при обході ламаної А1А2…Аn внутрішня частина багатокутника знаходиться з ліва, і із знаком мінус, якщо вона знаходиться справа. Вона і називається орієнтованою площею багатокутника А1А2…Аn. Таким чином, для правої СК орієнтована площа виявиться додатною при обході границі багатокутника проти годинникової стрілки.
Мал. 3 Отже, обчислення площі багатокутника звелося до знаходження орієнтованої площі трикутника. Розглянемо, як записати її за допомогою координат. Нехай S – орієнтована площа трикутника побудованого на векторах a=(x1,y1) і b=(x2,y2). Обчислимо її для даного розміщення векторів (мал. 4). Величина S тут додатна (пара векторів a=
(тут S1, S2, S3 – звичайні не орієнтовані площі). Розкриємо дужки в лівій частині рівності і виразимо 2S, отримаємо 2S=x1y2-x2y1 (1)
Мал. 4 Легко переконатись, що при інших варіантах розміщення векторів формула (1) також залишається правильною. Таким чином, орієнтована площа паралелограма, побудована на векторах a=(x1,y1) і b=(x2,y2), дорівнює x1y2-x2y1. Величина x1y2-x2y1 називається косим (або псевдоскалярним) добутком векторів а і b. Для «косого» добутку ми будемо використовувати позначення [a,b] . Ця назва пов’язана із властивістю косої симетрії: [a,b]=-[a,b] (Дане позначення використовується для векторного добутку, але на відміну від векторного добутку косий добуток – це скаляр). Так, як неорієнтована площа паралелограма, побудованого на векторах а і b, рівна Тепер, як і обіцяли, знайдемо в координатах кут між двома векторами. Нехай
Величина звичайного кута рівна модулю значення орієнтованого кута. Відмітимо, що всі відомості про орієнтовані кути і площі відносились до правої СК. Може таке статись, що для конкретної задачі краще використовувати ліву СК (вісь абсцис направлена в право, вісь ординат – вниз). При такому розміщені осей додатнім буде поворот за годинниковою стрілкою. З цією поправкою все вище сказане застосовується і до лівої СК. РІВНЯННЯ ЛІНІЙ Рівняння прямої, яка проходить через дві різні точки, які задані своїми координатами. Нехай на прямій задані дві точки Р1 з координатами (х1,у1) і Р2 з координатами (х2,у2). Відповідно вектор з початком т. P1 і кінцем в т. Р2 має координати (х2-х1,у2-у1). Якщо Р(х,у) – довільна точка нашої прямої, то координати вектора (х-х1)(у2-у1)-(у-у1)(х2-х1)=0 (3) або (у2-у1)х+(х1-х2)у+х1(у1-у2)+у1(х2-х1)=0 Остатню рівність запишемо так: ax+by+c=0 (4) де а=у2-у1, b=х1-х2, с= х1(у1-у2)+у1(х2-х1). Отже, будь-яку пряму можна задати рівнянням виду (4). В наступному пункті покажемо, що і навпаки, при будь-яких значеннях коефіцієнтів (крім а=b=0) рівняння такого виду задає на площині деяку пряму. Зауважимо, що при програмуванні формулу (3) не можна використовувати у вигляді відношення: Рівняння прямої можна записати і в параметричному вигляді. Будь-який вектор, з початком в т. Р1 і кінцем в довільній т. Р(х,у), який лежить на даній прямі, можна отримати з (x-x1)=t(x2-x1) і (y-y1)=t(y2-y1) Знайшовши звідси х і у, отримаємо систему параметричних рівнянь, яка задовольняє кожну точку нашої прямої.
І навпаки, якщо координати (х,у) точки Р задовольняють дані співвідношення, вектор Ця система, але із введеними обмеженнями значення t, буде задавати і відрізок Р1Р2, і промінь Р1Р2. Для відрізка |
, при якому вісь Ох накладається на Оу, здійснювався проти годинникової стрілки. Така СК називається правою. Надалі будемо говорити, що наша СК права. В такій СК напрямок повороту проти годинникової стрілки називають додатнім.
, або жирним курсивом латинською буквою, a. Для позначення довжини вектора (тобто довжини відповідного відрізка) будемо використовувати символ модуля (наприклад, 
). Два вектора називаються рівними, якщо вони накладаються паралельним перенесенням.
. Рівність двох векторів а= 
і b= 
еквівалентна рівності їх відповідних координат: ax=bx, ay=by.
, його напрямок співпадає з напрямком а, якщо t>0, і протилежний йому, якщо t<0. Це дозволяє нам вивести співвідношення колінеарних векторів(тобто однаково напрямлених, або протилежно напрямлених), підрозумівають під цим коефіцієнт їх пропорційності. За допомогою даного співвідношення зручно описувати порядок розміщення точок на прямій. Наприклад, умова 
означає, що точки А, В і С лежать на одній прямій, причому т. А лежить між В і С. Відмітимо ще, що вектор, співнапрямлений з даним вектором а і має задану довжину l можна представити таким чином 
. Надалі ми неодноразово будемо цим користуватися. В координатах перераховані операції над векторами записуються так:
, де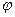 
- кут між даними векторами.
). Так як 
додатній для гострих кутів і від’ємний для тупих, кут між векторами гострий (тупий) в тому випадку, коли їх скалярний добуток додатній (від’ємний).
.
. На мал. 2 орієнтування кута між векторами 
і між векторами 
рівне по модулю, але перший з них від’ємний, а другий додатній. Для будь-яких векторів 
легко обчислити величину орієнтованого кута АОВ, знаючи величини кутів АОС і СОВ: вона рівна їх сумі з врахуванням знаків. Наприклад, при такому розміщенні векторів, як на мал. 2, кут АОС буде в сумі зі знаком плюс, а кут СОВ – з мінусом. Може статися, що при сумі рівних двох додатних (двох від’ємних) кутів результат стане більший за 
по модулю. Тоді, щоб отримати правильне значення кута, потрібно відняти (додати) 
. При цьому нам непотрібно розглядати різні випадки взаємного розміщення векторів. В цьому і є перевага використання орієнтованих кутів.
. Але при цьому отримаємо значення неорієнтованого кута і частина інформації (можливо важливої) буде нами втрачена. Крім цього, використання даної формули для програмування не завжди зручне. Наприклад, в мові програмування Паскаль, як і в багатьох інших мовах програмування з обернених тригонометричних функцій реалізована тільки функція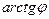 
. Покажемо, як можна знайти кут інакше, після того, як познайомимось з орієнтованою площею.
. Тобто її знак залежить від порядку перерахунку вершин. На мал. 2 трикутник АВС – прямокутний. Його орієнтована площа рівна 
(вона більша 0, так як пара 
і b= 
додатньо орієнтовані). Добудуємо наш трикутник до паралелограма ОАСВ з площею 2S (тут 
). Тоді площа прямокутника ОС1СС2 становитиме
, а знак 
співпадає із знаком орієнтованого кута 
).
. Знаючи тангенс кута між векторами, ми легко знайдемо кут між прямими на яких лежать а і b: він дорівнює 
. Щоб отримати сам кут між векторами, залишилось з’ясувати гострий він чи тупий. Це ми визначимо зі знаку скалярного добутку. Врахуємо ще, що знак орієнтованого кута співпадає із знаком косого добутку. Тоді отримаємо:
, якщо (a,b)=0, [a,b]>0;
, якщо (a,b)=0, [a,b]<0;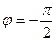
, якщо (a,b)>0;
, якщо (a,b)<0, [a,b]>=0;
, якщо (a,b)<0, [a,b]<0. (2)
становлять (х-х1,у-у1). За допомогою косого добутку умова колінеарності векторів 
можна виразити таким чином: 
, тобто
, так як, по-перше, навіть якщо всі координати заданих точок цілі числа, помилки дійсної арифметики при дії ділення не дозволяє перевірити за допомогою даного відношення, належність деякої точки даній прямій, а, по-друге, програма буде зупинена при діленні на нуль.
, шляхом множення вектора на деяке дійсне число t. Тоді для кожної з координат справедлива рівність
(5)
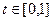(тобто х змінюється в діапазоні [x1,x2], а у – в діапазоні [у1,у2]), а для променя - 
.