 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Рівняння прямої, заданою однією з її точок і вектором нормалі до неї.
Нехай задана точка Ро прямої має координати (хо,уо), а деякий вектор нормалі n до неї (тобто вектор ортогональний до нашої прямої) – координатами (а,b). Якщо Р(х,у) довільна точка нашої прямої, тоді координати вектора
Очевидно, що рівняння (6) також легко звести до вигляду (4). Тоді видно, що коефіцієнти а, b у рівнянні (4) будуть координатами одного із векторів нормалі до нашої прямої. Звідси, випливає, що при будь-яких значеннях коефіцієнтів а, b і с (крім а=b=0) рівняння (4) задає пряму. Це буде пряма, перпендикулярна вектору (а, b) і яка проходить через точку, координати якої задовольняють (4). При а Не дивлячись на те, що на перший погляд умова задачі, може здатись надуманою, саме за допомогою її ми отримаємо хороший інструмент для розгляду цілого класу задач. В чому і переконаємось. Рівняння прямої, перпендикулярної даній, і що проходить через задану точку. Нехай задана точка Ро шуканої прямої має координати (хо,уо). Якщо Р(х,у) – довільна точка на цій прямій, то координати вектора (х2-х1)(х- хо)++(у2-у1)(у -уо)=0 (7) або (х2-х1)х+(у2-у1)у+( х2-х1)хо+( у2-у1)уо=0. Якщо наша пряма задана коефіцієнтами а, b і с свого рівняння, то легко побачити, що вектор її нормалі з координатами (а,b) колінеарний вектору Тоді, записавши косий добуток цих векторів, отримаємо: b(x-x0)-a(y-y0)=0 (8) 1.4. Рівняння прямої, що паралельна даній, та знаходиться на відстані r. Очевидно, що шуканих прямих дві. Вектор нормалі до даної прямої ортогональний і до кожної з паралельних прямих. Значить коефіцієнти а і b при х і у в рівнянні (4) для паралельних прямих такі самі, як і в заданій прямій. Залишається підібрати значення третього коефіцієнта. Позначимо його для однієї прямої с1, для другої – с2. Як вище було зазначено, для визначення цих коефіцієнтів достатньо знайти хоча б по одній точці на кожній із прямих. Візьмемо довільну точку Р(х0, у0) на заданій прямій (якщо пряма була задана не двома точками, то точку можна знайти за алгоритмом поданим в кінці п. 1.2). Проведемо через неї пряму, перпендикулярну даній. На паралельній прямі будемо шукати точку перетину (М(х1,у1)) з цим перпендикуляром (мал. 5). Нам відомий один вектор нормалі n=(а,b). Вектор Рівняння однієї із прямих отримане. В якості вектора нормалі для другої прямої можна взяти вектор –
Мал. 5 Рівняння бісектриси кута. Нехай вектор
Мал.. 6 З умови колінеарності вектора
При необхідності з (9) легко отримати коефіцієнти а, b і с для запису рівняння знайденої прямої у вигляді (4). 1.6. Рівняння кола. За означенням кола з центром в т. М0(х0,у0) і радіусом r, точка М(х,у) лежить на колі тоді і тільки тоді, коли відстань між точками М0 і М рівна r. Використавши формулу для обчислення квадрату відстані між двома точками, ми прийдемо до наступного рівняння кола: (х-х0)2+(у-у0)2=r2 (10) На практиці виявляється корисно знати і параметричне рівняння кола. Розглянемо перше коло з центром в початку координат. Якщо позначити t – кут між радіус-вектором x=х0+rcost y=у0+rsint (11) Покажемо ще, як можна визначити довжину l найменшої дуги кола, якщо кінці дуги (х1,у1) і (х2,у2). З курсу геометрії відомо, що довжина кола прямо пропорційна куту Дотична до кола. Нехай коло з центром у т. Р0(х0,у0) і радіусом r. Потрібно знайти рівняння дотичної до кола, яка проходить через т. Р1(х1,у1). Тут можливі три випадки. Якщо
Мал. 7 Ми будемо шукати а=х2-х1 і b=у2-у1 вектора Геометричний зміст косого добутку
Записуючи ці добутки в координатах отримаємо систему лінійних рівнянь відносно а і b:
Таку систему розв’язати вже неважко. Далі за точкою Р1(х1,у1) і направляючим вектором Для розв’язування цієї задачі є метод, в якому не потрібно навіть розв’язувати систему лінійних рівнянь. Проведемо з вершини Р2 прямого кута висоту Р2Р3 (мал. 7). З подібності трикутників Р1Р2Р0 і Р1Р3Р2 знайдемо довжини відрізків Р1Р3 і Р3Р2:
Тепер поступово знаходимо координати вектора
|



 рівні (х-хо, у-уо). Скалярний добуток ортогональних векторів
рівні (х-хо, у-уо). Скалярний добуток ортогональних векторів  можна виразити так:
можна виразити так: (6)
(6) 0 такою точкою буде, наприклад, точка
0 такою точкою буде, наприклад, точка  , при а=0 – точка
, при а=0 – точка  .
. дорівнюють (х-хо,у-уо). Цей вектор перпендикулярний вектору
дорівнюють (х-хо,у-уо). Цей вектор перпендикулярний вектору  , де Р1(х1,у1) і Р2(х2,у2) – точки на даній прямі. Тоді скалярний добуток ортогональних векторів
, де Р1(х1,у1) і Р2(х2,у2) – точки на даній прямі. Тоді скалярний добуток ортогональних векторів  можна виразити так:
можна виразити так: колінеарний йому, а його довжина r. Для визначеності будемо рахувати, що, як і на малюнку, нормаль лежить з того ж боку прямої, що і точка М. Тоді
колінеарний йому, а його довжина r. Для визначеності будемо рахувати, що, як і на малюнку, нормаль лежить з того ж боку прямої, що і точка М. Тоді  . Значить координати точки М дорівнюють
. Значить координати точки М дорівнюють  ,
,  . Підставимо їх у формулу (6), отримаємо
. Підставимо їх у формулу (6), отримаємо  .
. .
.
 і
і  беруть початок в точці
беруть початок в точці  . Знайдемо рівняння бісектриси кута Р1Р0Р2. Якщо ми поділимо кожен з векторів
. Знайдемо рівняння бісектриси кута Р1Р0Р2. Якщо ми поділимо кожен з векторів 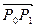 і
і  на його довжину, отримаємо при цьому вектори одиничної довжини. Вектор їх суми буде лежати на бісектрисі кута між ними (мал. 6). Координатами даного вектора будуть:
на його довжину, отримаємо при цьому вектори одиничної довжини. Вектор їх суми буде лежати на бісектрисі кута між ними (мал. 6). Координатами даного вектора будуть: .
.
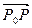 , де Р(х,у) – довільна точка на шуканій прямій, отримаємо рівняння бісектриси:
, де Р(х,у) – довільна точка на шуканій прямій, отримаємо рівняння бісектриси: (9)
(9) (М(х,у) – довільна точка, що лежить на колі) і віссю Ох, який вимірюється проти годинникової стрілки, то очевидно, що x=rcost, y=rsint. Отже, для довільного кола параметричні рівняння будуть мати такий вигляд:
(М(х,у) – довільна точка, що лежить на колі) і віссю Ох, який вимірюється проти годинникової стрілки, то очевидно, що x=rcost, y=rsint. Отже, для довільного кола параметричні рівняння будуть мати такий вигляд: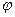 між векторами (х1-х0,у1-у0) і (х2-х0,у2-у0):
між векторами (х1-х0,у1-у0) і (х2-х0,у2-у0):  . А як знайти значення даного кута, було вже показано вище (потрібно тільки врахувати, що у випадку пошуку довжини меншої з двох дуг нас цікавить неорієнтований кут в діапазоні
. А як знайти значення даного кута, було вже показано вище (потрібно тільки врахувати, що у випадку пошуку довжини меншої з двох дуг нас цікавить неорієнтований кут в діапазоні  ).
).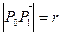 , то Р1 лежить на колі. Тоді у шуканій дотичній нам відома точка Р1 і нормаль
, то Р1 лежить на колі. Тоді у шуканій дотичній нам відома точка Р1 і нормаль  , її рівняння легко записується (див. п. 1.3). У випадку
, її рівняння легко записується (див. п. 1.3). У випадку  точок дотику дві. Позначимо одну з них Р2, ми отримаємо прямокутний трикутник Р0Р2Р1 (мал. 7). Можна спробувати знайти шукане рівняння, в «лоб». Якщо (х2,у2) – координати точки дотику Р2, то за теоремою Піфагора обчислюється довжина відрізка Р1Р2 (Р0Р2= r, Р0Р1 обчислюється за відомими координатами). Друге співвідношення для координат х2 і у2 – з рівняння кола (10). Обидва рівняння квадратні. Розв’язання даної системи представляє собою серйозні труднощі. Спробуємо обійтись без квадратних рівнянь, використавши скалярний і косий добуток векторів.
точок дотику дві. Позначимо одну з них Р2, ми отримаємо прямокутний трикутник Р0Р2Р1 (мал. 7). Можна спробувати знайти шукане рівняння, в «лоб». Якщо (х2,у2) – координати точки дотику Р2, то за теоремою Піфагора обчислюється довжина відрізка Р1Р2 (Р0Р2= r, Р0Р1 обчислюється за відомими координатами). Друге співвідношення для координат х2 і у2 – з рівняння кола (10). Обидва рівняння квадратні. Розв’язання даної системи представляє собою серйозні труднощі. Спробуємо обійтись без квадратних рівнянь, використавши скалярний і косий добуток векторів.
 . Як було зазначено вище, довжини сторін прямокутного трикутника Р0Р2Р1 легко знайти. Визначимо скалярний добуток векторів
. Як було зазначено вище, довжини сторін прямокутного трикутника Р0Р2Р1 легко знайти. Визначимо скалярний добуток векторів  і
і  :
:  .
. - подвоєння площі трикутника Р0Р2Р1, взятої із знаком плюс для однієї з точок і з мінусом – для другої.
- подвоєння площі трикутника Р0Р2Р1, взятої із знаком плюс для однієї з точок і з мінусом – для другої. .
.
 записуємо рівняння дотичної. Задача розв’язана. Якщо нам потрібно ще знайти і координати точки дотику, то це можна зробити, використавши координати т. Р1 і знайдені координати
записуємо рівняння дотичної. Задача розв’язана. Якщо нам потрібно ще знайти і координати точки дотику, то це можна зробити, використавши координати т. Р1 і знайдені координати  .
. ;
; 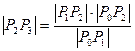 .
. , точки Р3(х3,у3) і, на кінець використовуючи відомі координати вектора n=(y0-y1, x1-x0), перпендикулярного прямій Р1Р3, координати точки Р2:
, точки Р3(х3,у3) і, на кінець використовуючи відомі координати вектора n=(y0-y1, x1-x0), перпендикулярного прямій Р1Р3, координати точки Р2: