 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ВЗАЄМНЕ РОЗМІЩЕННЯ ТОЧОК І ФІГУР
2.1. Розміщення точки відносно прямої, променя або відрізка. В першу чергу нас цікавить належність даної точки Р(х,у) вказаному геометричному об’єкту, рівняння якого нам відоме. Щоб відповісти на це запитання для прямої, достатньо підставити координати заданої точки в рівняння прямої (3) або (4). Рівність нулю значення отриманого виразу (для дійсних координат або коефіцієнтів рівняння перевірку на рівність нулю необхідно здійснювати з урахуванням похибки) означає, що точка належить даній прямі. Якщо значення виразу менше нуля, то точка належить одній півплощині, а більше нуля – іншій. Дійсно рівняння (3) отримаємо за умови, що пряма проходить через точки Р1(х1, у1) і Р2(х2, у2). Зауважимо, що ліва частина (3) – це значення косого добутку векторів Якщо пряма задана двома своїми точками, для розв’язування задачі достатньо обчислити значення косого добутку, а рівняння прямої записувати не потрібно. У випадку перевірки належності точки променю при Нехай нам тепер необхідно визначити, на якій відстані знаходиться задана точка до прямої, променя, відрізка. Формулу відстані від точки до прямої отримуємо із співвідношення двох способів обчислення площі трикутника:
Мал. 8 Для променя або відрізка вказаний спосіб знаходження відстані потрібно дещо відредагувати. Точка H (мал. 8) лежить на промені Р1Р2 в тому випадку, коли скалярний добуток 2.2. Взаємне розміщення двох точок відносно прямої. В багатьох випадках потрібно з’ясувати, по одну чи різні сторони відносно прямої лежать дві точки Р1 і Р2, задані своїми координатами. Виберемо на прямій дві довільні точки, що не співпадають – Р3 і Р4 (ними можуть бути якраз дві точки, що задають нашу пряму). Тоді, якщо косі добутки 2.3. Взаємне розміщення двох прямих, або променів і відрізків. Легко з’ясувати, чи перетинаються дві прямі чи вони паралельні. Нагадаємо ще раз, що умова колінеарності двох векторів – це рівність нулю їх косого добутку. Якщо прямі задані рівняннями а1х+b1у+с1=0 і а2х+b2у+с2=0, то зручно перейти до їх нормалей: n1=(а1, b1) і n2=(а2, b2). Тоді умова колінеарності нормалей (а значить, і паралельності прямих): [n1,n2]=a1b1-a2b2=0. Якщо прямі задані парами точок, то таким ж методом перевіряється колінеарність направляючих векторів. Перевірка наявності перетину прямої і відрізка нами фактично була показана при розв’язуванні задачі 2.2. Нехай пряма і відрізок перетинаються в одній точці. Знайдемо її. Позначимо кінці відрізка Р1(х1, у1) і Р2(х2, у2). Нехай Р3(х3, у3) і Р4(х4, у4) – дві точки на прямій, а М – шукана точка перетину (мал. 9). Опустимо з кінців відрізка перпендикуляри на пряму P1H1 і P2H2. Трикутники Р3Р1Р4 і Р3Р2Р4 мають спільні основи. Звідси випливає, що відношення їх площ дорівнює відношенню їх висот
Мал. 9 Остатня рівність випливає з подібності трикутників P1H1M і P2H2M звідси отримуємо:
В даній формулі враховано і те, що одна з площ може бути рівна нулю, і те, що вказані площі мають однакові знаки тоді, коли точки Р1 і Р2 лежать по одну сторону відносно прямої Р3Р4 (тобто коли вектор
(Тут ми використали властивість лінійності косого добутку: Таким чином, ми знайшли точку перетину прямої і відрізка. Для знаходження перетину двох прямих на одній з них вибираються дві довільні точки Р1 і Р2, на другій – Р3 і Р4. Можливо, виведення формули (13) не зовсім елементарне, але саму формулу легко запам’ятати, якщо зрозумілий її геометричний зміст. Так, якщо відрізки Р1Р2 і Р3Р4 перетинаються, то площа чотирикутника Р1Р2Р3Р4 за відомою формулою є половина добутку діагоналей на синус кута між ними. Тобто за абсолютною величиною косого добутку векторів 2.4. Взаємне розміщення двох відрізків і променів. Перевірити перетин двох відрізків (як правило нас найчастіше цікавить лише сам факт перетину) не складно, коли знову ж використати косий добуток. Нехай перший відрізок заданий точками Р1 і Р2, а другий – Р3 і Р4. відрізки перетинаються тоді, коли, по-перше, перетинаються прямокутники, які обмежують дані відрізки, по-друге, кінці кожного відрізка лежать по різні сторони прямої на якій лежить інший відрізок. Перша умова дозволяє не розглядати окремий випадок, коли відрізки лежать на одній прямі. Позначимо xmax1 і xmin1 максимальну і мінімальну з х-координат першого відрізка, xmax2 і xmin2 – другого відрізка. Для у-координат аналогічно уmax1, уmin1, уmax2, уmin2. Тоді умову перетину формально можна записати: 1) xmax1 2) косі добутки 3) аналогічно Якщо факт перетину двох відрізків встановлено, то точка перетину шукається, як і в задачі 2.3. Для відрізків однієї прямої їх перетин (точку або відрізок) можна знайти шляхом розрахунку значень двох скалярних добутків аналогічно задачі 2.1 або за допомогою порівняння координат кінців відрізка. Введемо тепер поняття відстані між двома відрізками, які не перетинаються, як мінімальна серед відстаней між всіма парами точок двох відрізків. Нескладно зрозуміти, що відстань дорівнює відстані від кінця одного з відрізків до другого відрізка (задача 2.1). Тому для розв’язування даної задачі достатньо обчислити відповідні відстані для кожної з чотирьох точок кінців відрізків і вибрати з них мінімальне. Для перевірки наявності перетину двох променів Р1Р2 і Р3Р4 потрібно розглянути взаємне розміщення двох прямих. Якщо косий добуток Якщо прямі Р1Р2 і Р3Р4 перетинаються в одній точці М ( 2.5. Взаємне розміщення кола і прямої. Пряма може перетинати коло в двох точках, дотикатись до нього, або не мати спільних точок з колом. Дані випадки легко визначити. Потрібно знайти відстань від центру кола до даної прямої (за допомогою формули відстані від точки до прямої, див. 2.1). Якщо дана відстань (позначимо її l) менша за радіус кола r, то пряма перетинає коло в двох точках, якщо рівна йому, то пряма дотикається до кола, а якщо більша за радіус, то спільних точок вони не мають. В остатньому випадку нас може цікавити відстань від прямої до кола. Вона рівна l- r. Більш складнішою є задача пошуку спільних точок прямої і кола. Випадок дотичної був розглянутий нами в п. 1.7. Нехай тепер пряма перетинає коло в двох точках. Координати цих точок можна знайти за наступним алгоритмом (мал. 10). Знайдемо вектор n нормалі до прямої. Відкладемо в напрямку цього вектора вектор
Мал. 10 2.6. Взаємне розміщення двох кіл. Два різних кола також можуть перетинатися в двох точках, дотикатися одне до одного і не мати спільних точок. В остатньому випадку одне із кіл може лежати в середині іншого (назвемо такі кола вкладеними) або кожне із кіл лежить зовні іншого. Перевірка перетину або дотику аналогічна попередній задачі здійснюється шляхом порівняння відстаней між центрами кіл (позначимо її l) з їх радіусами, якщо Координати точки дотику кіл знайти дуже просто. Центри кіл О1(х1, у1) і О2(х2, у2) задають пряму на якій лежить і точка дотику Р (х3, у3). Будемо вважати, що т. О1 є центром кола з більшим радіусом. Тоді вектор Для пошуку координат двох точок перетину кіл використаємо механізм, вже описаний в задачі 1.7. Розглянемо трикутник О1О2Р (мал. 11). В трикутнику відомі всі три довжини сторін (r1>r2 і l). Проведемо в трикутнику висоту PH. В отриманому прямокутному трикутнику О1HР невідомі довжини катетів. Знайдемо О1H, записавши теорему косинусів для трикутника О1О2Р:
Мал. 11 Зауважимо, що при розв’язувані задач 1.7, 2.5 і 2.6 ми використовуємо «покрокові» алгоритми. А саме, аналізуючи малюнок, виділяємо ланцюжок об’єктів (вектори точки та ін.). Фактично ми послідовно встановлюємо параметри об’єктів виділених нами на малюнку. Ланцюжок обчислень повинен привести нас до відповіді, при цьому кожен крок дуже простий і повністю очевидний. Не виключено, що задача має і більш коротший аналітичний розв’язок (наприклад, розв’язування системи рівнянь). Але «покроковий» метод в силу своєї наочності, дозволяє контролювати кожний крок розв’язку, а саме ця властивість може відіграти важливу роль при перевірці алгоритму і налагодженні програми. 2.7. Перевірка належності точки внутрішній області багатокутника. Нехай М – деяка точка площини. Потрібно визначити її місцезнаходження відносно замкнутої ламаної. Розглянемо спочатку випадок опуклого багатокутника. Нехай задані координати вершин багатокутника Р0,Р1,…,Рn-1 перераховані в порядку його обходу проти годинникової стрілки. При такому обході багатокутник лежить зліва від границі. Отже, якщо точка М лежить всередині багатокутника, то орієнтований кут між векторами Розглянемо тепер довільний багатокутник. Проведемо горизонтальний промінь з точки М, наприклад, вліво. Так, як багатокутник обмежений, то завжди легко взяти на промені точку Р(х,у), яка не належить йому. Далі підрахуємо кількість перетинів відрізка РМ з границею багатокутника. Якщо ця кількість рівна нулю, або парна, то точка М лежить за межами багатокутника, в протилежному випадку – всередині нього. Кількість перетинів відрізка РМ з границею ми підрахуємо, розглянувши по черзі перетин відрізка РМ з кожною ланкою ламаної. При цьому можливі такі випадки. 1) Одна з ланок ламаної повністю лежить на відрізку РМ. 2) Ланка ламаної дотикається до відрізка РМ. 3) М лежить на одній із ланок ламаної. В остатньому випадку М належить границі багатокутника, і підрахунку загального числа перетинів не потребує. Для двох перших випадків зробимо наступне: в першому випадку на перетин не будемо звертати увагу. В другому – додатково перевіримо «нижнім» чи «верхнім» кінцем ланки ламаної дотикається до відрізка РМ. Якщо точка дотику є «нижнім» кінцем ланки, то перетин ігнорується, а якщо «верхнім» - то зараховується. Враховуючи це, отримаємо, що дотик відрізка РМ до границі багатокутника в одних точках ігнорується, а в інших точках рахується двічі. Це не змінить парності числа перетинів, а тільки вона важлива при пошуку відповіді в даній задачі. Якщо ж відрізок дійсно перетинає ламану в її вершині, то, за нашою домовленістю, число перетинів якраз збільшиться на одиницю (перетин з верхнім ребром зарахований не буде, а з нижнім – буде). Наприклад, на мал.12 кількість перетинів дорівнює чотирьом (дотик зараховано два рази), а для нижньої точки – трьом (дотик неврахований, а перетин у вершині ламаної врахований лише один раз).
Мал. 12
|



 і
і  . Його знак визначає орієнтацію цієї пари векторів, інакше кажучи, належність точки Р одній із півплощин (а при рівності нулю – належність прямій).
. Його знак визначає орієнтацію цієї пари векторів, інакше кажучи, належність точки Р одній із півплощин (а при рівності нулю – належність прямій).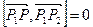 (Р1 – початок променя, Р2 будь-яка точка на промені) корисно знайти і скалярний добуток цих векторів. Якщо він менший нуля, Р1 лежить на прямій між Р2 і Р, звідси Р не належить променю. Щоб в аналогічній ситуації впевнитись належності точки Р відрізку Р1Р2, необхідно обчислити ще і значення скалярного добутку
(Р1 – початок променя, Р2 будь-яка точка на промені) корисно знайти і скалярний добуток цих векторів. Якщо він менший нуля, Р1 лежить на прямій між Р2 і Р, звідси Р не належить променю. Щоб в аналогічній ситуації впевнитись належності точки Р відрізку Р1Р2, необхідно обчислити ще і значення скалярного добутку  . Якщо воно невід’ємне, то точка Р лежить на відрізку.
. Якщо воно невід’ємне, то точка Р лежить на відрізку. (див. мал. 8). Тобто відстань b від точки Р до прямої, заданої координатами точок Р1 і Р2, можна обчислити, як відношення модуля косого добутку векторів
(див. мал. 8). Тобто відстань b від точки Р до прямої, заданої координатами точок Р1 і Р2, можна обчислити, як відношення модуля косого добутку векторів  і
і  до довжини відрізка Р1Р2.
до довжини відрізка Р1Р2.
 . Для відрізка Р1Р2 ясно, потрібно ще і виконання умови
. Для відрізка Р1Р2 ясно, потрібно ще і виконання умови  . Тоді можна застосувати формулу відстані від точки до прямої. В противному випадку відстань до променя (відрізка) буде дорівнювати відстані від точки до початку променя (до найближчого кінця відрізка).
. Тоді можна застосувати формулу відстані від точки до прямої. В противному випадку відстань до променя (відрізка) буде дорівнювати відстані від точки до початку променя (до найближчого кінця відрізка). і
і  мають різні знаки, тобто
мають різні знаки, тобто  , то точки лежать по різні сторони прямої, якщо знаки співпадають – то по одну сторону, якщо одне із значень 0, то відповідна точка лежить на прямій. Взагалі ця задача є частиною, більш складної задачі.
, то точки лежать по різні сторони прямої, якщо знаки співпадають – то по одну сторону, якщо одне із значень 0, то відповідна точка лежить на прямій. Взагалі ця задача є частиною, більш складної задачі. і
і  . Але площа (орієнтована) трикутника Р3Р1Р4 – це
. Але площа (орієнтована) трикутника Р3Р1Р4 – це  , аналогічно обчислюється площа Р3Р2Р4. Тобто
, аналогічно обчислюється площа Р3Р2Р4. Тобто 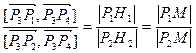 .
.
 (12)
(12) і
і  співнапрямлені). Ми знайшли у якому відношенні ділиться даний відрізок точкою М. З іншої сторони,
співнапрямлені). Ми знайшли у якому відношенні ділиться даний відрізок точкою М. З іншої сторони,  . Підставимо ці співвідношення в (12). Виразимо
. Підставимо ці співвідношення в (12). Виразимо 
 (13)
(13) ), яке легко вставити, якщо записати цю рівність в координатах). Тепер, знаючи координати точки Р1 і вектора
), яке легко вставити, якщо записати цю рівність в координатах). Тепер, знаючи координати точки Р1 і вектора  і
і  , який стоїть в знаменнику формули (13), – це подвоєна площа чотирикутника Р1Р2Р3Р4. В чисельнику ми маємо подвоєну площу трикутника Р3Р4Р1.
, який стоїть в знаменнику формули (13), – це подвоєна площа чотирикутника Р1Р2Р3Р4. В чисельнику ми маємо подвоєну площу трикутника Р3Р4Р1. xmin2, xmax2
xmin2, xmax2  і
і  мають різні знаки, тобто
мають різні знаки, тобто  ;
; .
. рівний нулю, це означає, що промені лежать на паралельних прямих. Якщо це дві різні прямі, то вектори
рівний нулю, це означає, що промені лежать на паралельних прямих. Якщо це дві різні прямі, то вектори  і
і  не колінеарні, значить, косий добуток
не колінеарні, значить, косий добуток  не дорівнює нулю. В цьому випадку промені не перетинаються. Коли промені лежать на одній прямі, то за допомогою знаку скалярного добутку
не дорівнює нулю. В цьому випадку промені не перетинаються. Коли промені лежать на одній прямі, то за допомогою знаку скалярного добутку  можна зрозуміти, в одну чи різні сторони вони напрямлені. В першому випадку скалярний добуток буде додатнім, а в другому – від’ємний. Якщо промені співнапрямлені, то визначити, який із променів являється їх перетином, можна, обчислити значення скалярного добутку
можна зрозуміти, в одну чи різні сторони вони напрямлені. В першому випадку скалярний добуток буде додатнім, а в другому – від’ємний. Якщо промені співнапрямлені, то визначити, який із променів являється їх перетином, можна, обчислити значення скалярного добутку  . Коли скалярний добуток більший нуля, перетином являється промінь Р3Р4, в протилежному випадку – промінь Р1Р2. У випадку, коли промені протилежнонапрямлені їх перетином може бути відрізок Р1Р3, і тоді початок кожного з променів лежить в середині другого:
. Коли скалярний добуток більший нуля, перетином являється промінь Р3Р4, в протилежному випадку – промінь Р1Р2. У випадку, коли промені протилежнонапрямлені їх перетином може бути відрізок Р1Р3, і тоді початок кожного з променів лежить в середині другого:  , або одна точка Р1=Р3:
, або одна точка Р1=Р3: 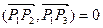 , або вони не мають спільних точок
, або вони не мають спільних точок  .
.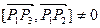 ), то знайти цю точку можна, як і в задачі 2.3. Пізніше потрібно перевірити, чи т. М належить кожному із променів:
), то знайти цю точку можна, як і в задачі 2.3. Пізніше потрібно перевірити, чи т. М належить кожному із променів:  і
і  .
. довжини l. Обчислимо відстань
довжини l. Обчислимо відстань  . Від т. А вздовж прямої відкладемо в обидва боки вектори довжини
. Від т. А вздовж прямої відкладемо в обидва боки вектори довжини  . Їх кінці дадуть нам дві шукані точки Р1 і Р2. Кожний крок даного алгоритму розглядався нами окремо раніше. Зауважимо тільки те, що на першому кроці необхідно правильно вибрати один з двох можливих напрямків нормалі до прямої. Для цього достатньо перевірити, що скалярний добуток
. Їх кінці дадуть нам дві шукані точки Р1 і Р2. Кожний крок даного алгоритму розглядався нами окремо раніше. Зауважимо тільки те, що на першому кроці необхідно правильно вибрати один з двох можливих напрямків нормалі до прямої. Для цього достатньо перевірити, що скалярний добуток  , де М – довільна точка прямої.
, де М – довільна точка прямої.
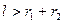 або
або  , то кола спільних точок не мають. Друга умова показує, що одне коло лежить всередині іншого. При заміні знаку в будь-якій з цих двох нерівностей на рівність, ми отримаємо дотикання даних кіл (зовнішнє або внутрішнє дотикання). Якщо
, то кола спільних точок не мають. Друга умова показує, що одне коло лежить всередині іншого. При заміні знаку в будь-якій з цих двох нерівностей на рівність, ми отримаємо дотикання даних кіл (зовнішнє або внутрішнє дотикання). Якщо  , то кола мають дві точки перетину.
, то кола мають дві точки перетину. співнапрямлений з вектором
співнапрямлений з вектором  . Довжини обох векторів також відомі, тому шукані координати дорівнюють:
. Довжини обох векторів також відомі, тому шукані координати дорівнюють:  . Перевірте, якщо
. Перевірте, якщо  то у випадку вкладення кіл отримана формула потребує корекції.
то у випадку вкладення кіл отримана формула потребує корекції. . Звідси,
. Звідси,  . За теоремою Піфагора
. За теоремою Піфагора  . Тепер послідовно знаходимо: вектор
. Тепер послідовно знаходимо: вектор  , точку H за відомою т. О1 і вектором
, точку H за відомою т. О1 і вектором  , вектор n=(у2-у1, х1-х2), перпендикулярний О1О2, вектор
, вектор n=(у2-у1, х1-х2), перпендикулярний О1О2, вектор  , а також точку Р за відомою точкою H і вектором
, а також точку Р за відомою точкою H і вектором  . Замінивши в остатній дії вектор
. Замінивши в остатній дії вектор 
 і
і  від’ємний. Тому нам достатньо обчислити величини косих добутків
від’ємний. Тому нам достатньо обчислити величини косих добутків  , i=0,1,…,n-1; значення i+1 береться по модулю n. Якщо всі отримані при цьому значення менші нуля, то точка М внутрішня. Якщо ж одне з них рівне нулю, а всі інші менші нуля, тоді М належить границі багатокутника (переконайтесь, що просто рівність нулю одного із значень недостатньо). В протилежному випадку точка М лежить поза межами багатокутника.
, i=0,1,…,n-1; значення i+1 береться по модулю n. Якщо всі отримані при цьому значення менші нуля, то точка М внутрішня. Якщо ж одне з них рівне нулю, а всі інші менші нуля, тоді М належить границі багатокутника (переконайтесь, що просто рівність нулю одного із значень недостатньо). В протилежному випадку точка М лежить поза межами багатокутника.