 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Поняття многокутника та його елементів
Мета вивчення теми: - систематизувати і узагальнити відомості про геометричну фігуру – многокутник (трикутник, прямокутник, квадрат); - формувати вміння побудови многокутника; - розвивати уявлення про многокутник, його вершини, сторони і кути; сформулювати властивості сторін і кутів трикутника, прямокутника, квадрата; - розвивати просторові уявлення учнів; - виховувати графічну культуру. Знання і вміння: Знати : - означення многокутника, назви його елементів, означення периметра; - означення трикутника, прямокутника, квадрата, властивості їх кутів та сторін, формули знаходження їх периметрів. Вміти: - виконувати побудову многокутника; - визначати довжину його сторін, величину кутів; - застосовувати формули обчислення периметра при розв'язуванні задач.
Методика викладу Поняття многокутника є одним з найважливіших у геометрії. Перші уявлення про цю геометричну фігуру та її елементи учні дістають у початковій школі. Завдання вчителя на даному етапі – узагальнити і систематизувати їх, поглибити і розширити. Необхідно удосконалити графічні уміння й навички учнів, підвести їх до самостійних узагальнень. Окремим видом многокутника є трикутник. У пояснювальному тексті підручника трикутник визначається, як фігура, яка складається з відрізків, що попарно з'єднують три точки, які не лежать на одній прямій. Вводиться поняття сторони, вершини трикутника, його символічне позначення. Відповідні записи учні повинні зробити в зошитах. Далі учням даються завдання: 1. Дати означення периметра трикутника. 2. Накреслити довільний трикутник і знайти його периметр. 3. З'ясувати, як можна знайти одну із сторін трикутника, коли відомо його периметр і дві інші сторони? Щоб учні свідомо засвоїли властивість сторін трикутника – сума двох будь-яких сторін трикутника більша за третю сторону, – варто провести практичну роботу за планом: 1. Визначити довжини сторін трикутника. 2. Обчислити суму двох будь-яких сторін трикутника. 3. Порівняти одержаний результат (число) з довжиною третьої сторони. 4. Зробити висновок. Вчителю треба наголосити на тому, що кожний з учнів працював з своєю моделлю трикутника, але всі вони отримали однаковий результат, який виражає властивість сторін трикутника. Ця властивість має місце для довільного трикутника (гострокутного, тупокутного, прямокутного), тобто має масовий характер. Питання про суму кутів трикутника, суму гострих кутів прямокутного трикутника в пояснювальному тексті не дається. Однак все ж таки доцільно розглянути їх п'ятикласниками. Так, зокрема, розв'язання вправ №174, 175 дає можливість вчителю сформулювати (учням бажано записати у зошити) властивість кутів трикутника. Введення поняття рівнобедреного і рівностороннього трикутників на цьому етапі навчання підготує учнів до розгляду питання про обчислення периметра цих фігур. В цілому така робота сприяє розвитку логічного мислення, розширенню діапазону їх математичних знань. Інший відомий учням вид многокутника – чотирикутник (прямокутник, квадрат). Модель діяльності вчителя і учнів може бути такою. Учні поділяють сторінку на 2 частини: у лівій будуть записи стосовно прямокутника, у правій – квадрата. Спочатку вони під керівництвом вчителя розглядають основні питання, повязані з прямокутником, роблять відповідні записи для квадрата. Можна колективно розглядати прямокутник і квадрат паралельно. Основні питання, які треба з'ясувати, такі: 1. Назвати предмети з навколишнього середовища, що мають форму прямокутника і квадрата. 2. Накреслити фігуру, про яку йдеться в задачі: ''Під час екологічного суботника учням треба було скопати ділянку прямокутної (квадратної) форми. Знайти периметр ділянки, якщо її довжина 25 м, а ширина 10 м (довжина сторони квадрата 25 м). Умови задач доцільно записати в таблицю. 3. Який чотирикутник називається прямокутником (квадратом)? 4. Що можна сказати про кути цієї фігури? 5. Що можна сказати про довжини сторін цієї фігури? 6. Позначити сторони фігури через a i b (для квадрата - a). 7. Записати формулу для обчислення периметра прямокутника (квадрата). 8. Обчислити периметр фігури відповідно до умови задачі. 9. Чи справджуються отримані формули для обчислення периметра для довільного прямокутника (квадрата)? 10.Що можна сказати про периметр прямокутника і квадрата, якщо довжина прямокутника співпадає зі стороною квадрата? Орієнтовний зразок запису в зошитах учнів наведено у наступній таблиці:
Приступаючи до розв’язування вправ, вчителю слід наголосити, що у випадку, коли сторони прямокутника виражені в різних одиницях вимірювання, то перед тим, як перейти до обчислення периметра прямокутника, треба звести їх до одних і тих самих одиниць вимірювання. З методичного боку доцільно спочатку розглянути з учнями вправи на обчислення периметра многокутника, використовуючи різні формули. Згодом перейти до розв’язування обернених задач: за периметром і однією стороною прямокутника знайти другу сторону; за периметром знайти сторону квадрата. |



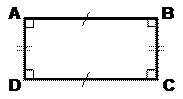
 2.
2. 
 7. P= a+b+ a+b=2a+2b=2(a+b)
7. P= a+b+ a+b=2a+2b=2(a+b)