 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Глава 2. Статистический контроль эффективности мероприятий по обеспечению безопасности.
Так как одним из наиболее объективных методов оценки безопасности работ в техносфере является статистически контроль соответствующих показателей, то вызывает интерес изучение возможности его использования и для определения эффективности мероприятий, направленных на предупреждение аварийности и травматизма. Иными словами, целесообразно обосновать условия применимости этих методов для оценки результативности таких мероприятий, как аттестация рабочих мест, проведение технических освидетельствований и обследований технологического оборудования, проверка знаний и практических навыков персонала. На первый взгляд может создаться впечатление, что при решении этой задачи не следует ожидать трудностей, подобных контролю безопасности эксплуатации вновь созданного оборудования на головном объекте. Ведь не исключено, что подготовка обоснованного ответа по высказанному предположению, потребует всего лишь наблюдений за конкретными технологическими процессами, отличающимися степенью внедрения мер по «технике безопасности» и регистрации данных об аварийности и травматизме при их проведении. Тогда как их обработка может выявить факты расхождения в значениях выбранных показателей безопасности и оценить его величину. Однако более углубленный анализ особенностей статистического контроля эффективности мероприятий по повышению безопасности указывает на необходимость решения ряда дополнительных задач. Эти, естественные для статистических методов, задачи касаются оценки достоверности полученных выводов, определяемой как объемами и ошибками проводимых наблюдений, так и требуемыми уровнями значимости сделанных суждений. Следовательно, корректное решение таких задач предполагает разработку и системный анализ соответствующих моделей. Рассмотрим возможность решения наиболее сложной и актуальной задачи статистического контроля эффективности мероприятий по предупреждению происшествий, непосредственно в ходе внедрения мероприятий по их предупреждению в некоторый технологический эксплуатационный процесс. Ее актуальность обусловлена экономическими соображениями, а сложность вызвана, по меньшей мере, двумя обстоятельствами. С одной стороны, в процессе внедрения таких мероприятий, например, проведения целевых освидетельствований электрооборудования или аттестации рабочих мест, будут существовать две группы исследуемых объектов: подвергнутые их воздействию и – не подвергнутые, причем соотношение между ними будет непрерывно изменяться С другой стороны, так как в изучаемый период происшествия могут появляться на оборудовании каждый такой группы, то это обстоятельство следует учитывать в последующем оценивании путем цензурирования выборки исследуемых объектов и происшествий. Учитывая все это, при разработке модели, необходимой для обоснования процедуры статистического контроля эффективности мероприятий по повышению безопасности техносферы, будем исходить из уже используемых предположений: 1. Возникновение происшествия на отдельно взятых рабочих местах или элементах оборудования является редким случайным событием; 2. Их число при массовых работах подчинено распределению Пуассона и пропорционально длительности изучаемого периода; 3. Появление происшествия на одном объекте не влияет на возможность их возникновения на других. Из принятых предположений следует экспоненциальность распределения времени между появлением отдельных происшествий, выражающаяся в том, что если до какого то времени t их не было где-то, то вероятность их появления там же в любой последующий период времени τ такова, какой она была и в соответствующие по длительности предыдущие периоды. Это свойство справедливо для процесса, характеризуемого сравнительно небольшой продолжительностью по отношению к времени «наработки» на происшествие, что обусловлено возможными изменениями качества техники вследствие ее доработок и старения или уровня обученности людей, из-за их дополнительной подготовки. Для проведения статистической оценки значений средней длительности «наработки» на происшествие ниже будет использован метод максимального правдоподобия. В предложении о независимости функционирования исследуемых объектов из числа безопасности, может быть составлено выражение для соответствующей функции. ЕЕ значение будет определяться произведением вероятностей Qi возникновения происшествий на тех объектов, где они случились в изучаемый период, и вероятностей Pδi их не возникновения на остальных объектах. Как следует из природы экспоненциального распределения времени между происшествиями, график которого приведен на рисунке 1, значение Qi определяется ординатой плотности вероятности их проявления к концу периода времени наблюдения tni : Qi (ωпр ,tпi ) = ωпр e -ωпрtпi , (12) а величина Pδi – площадью под участком этой кривой, лежащей правее точки t0i :
Pδi = e -ωпрtпi (13) где tni – продолжительность времени от начала наблюдении за объектами до момента возникновения происшествия на i-м объекте; t0i – длительность изучаемого периода или его время от начала функционирования объекта до момента внедрения на нем оцениваемых мероприятий.
Рисунок 1– Экспоненциальное распределение времени  Оценкой максимального правдоподобия времени средней «наработки» на происшествие любым из групп N объектов, подвергнутых или не подвергнутых мероприятий, будет такое значение величины 1/ ωпр , при котором соответствующая функция L(ωпр ) принимает максимальное значение. Если в изучаемый период было зарегистрировано m происшествий, то функция правдоподобия определяется перемножением вероятностей (12) и (13): L(ωпр )=
где Очевидно, что для количества происшествий m≥1 выражение для оценивания величины средней «наработки на происшествие» имеет следующий вид: τ̂пр = 1/ ω̂пр = где
После определения общей для всех N объектов «наработки» на происшествие возможно и выявление эффективности исследуемых здесь мероприятий, которая может проявляться в изменении длительности такой «наработки». Факт же наличия статистически значимого прироста ее оценки на объектах с уже внедренными мероприятиями, должен быть установлен принятием одной из следующих двух статистических гипотез, –так называемой, «нулевой» H0 и «альтернативной» ей Hа :
H0 / τ̕пр = τпр ; Ha / τ̕пр ˃ τпр , (16) где τ̕пр , τпр продолжительность «наработки» на происшествие на объектах, подверженных и не подверженных внедрению мероприятий по повышению безопасности, соответственно. Для проверки справедливости выдвинутой гипотезы, необходимо знать закон распределения входящих в нее параметров или линейно связывающей их функции. При неизвестном действительном значении математического ожидания «наработки» на происшествие τпр в качестве такой функции может быть использована следующая случайная величина, приблизительно распределенная по нормальному закону: Z=( τ̕пр – τпр ) / где m̕ m – число происшествий, учтенных соответственно на объектах с внедренными и не внедрёнными мероприятиями по повышению безопасности. Из структуры последней формулы видно, что причиной «приблизительно нормального» распределения статистики Z служит знаменатель, «нелинейное» влияние которого в более строгом ее аналитическом выражении обычно компенсируется введением довольно громоздкого количеством зарегистрированных происшествий, а роль – уменьшением смещения между оценками τ̕пр , τпр и действительным значением «наработки» на происшествие при их большой дисперсии. Однако для пуассоновского распределения оценок m̕ и m, квадрат математического ожидания которого одновременно является и дисперсией, это смещение, как правило, невелико. Оказывается, что погрешность такого упрощённого представления Z обычно несущественна для значения параметра ∆= τ̕пр – τпр , соответствующей (1–γ)100%-ной доли площади под плотностью ее распределения, т.е в тех случаях, которые рассматриваются при проверке статистической гипотезы о равенстве средних величин. Это означает, что при принятых выше предположениях, решение о справедливости гипотезы Ha может быть принято лишь в том случае, когда значение ɀ превысит (1–γ)100% квантиль нормально распределенной величины. В противном случае для принятия этой гипотезы потребуется проведение дополнительных исследований. Графическая интерпретация плотностей распределения случайного прироста «наработки» на происшествие ∆= τ̕пр – τпр , отличающихся числовыми характеристиками конкурирующих гипотез H0 и Hа представлена на рисунке 2. Изображенная там левая «палатка» соответствует нулевой гипотезе, а правая – альтернативной.
Рисунок 2 – Плотность распределения параметра ∆: 1–H0 :∆=0; 2– Ha :∆˃0; 3– ошибка 1-го рода; 4– ошибка 2-го рода
Обозначенная на горизонтальной оси точка ∆кр является критическим значением параметра ∆ и определяется допустимыми значениями ошибок 1-го и 2-го рода . Величины соответствующих вероятностей равны заштрихованным областям, расположенным по обе стороны от ∆кр . В качестве решающего правила, необходимого для принятия одной из конкурирующих гипотез, может быть использована следующая критериальная зависимость: если ∆=τ̂̕пр –τ̂пр ≤∆кр , то справедливая нулевая гипотеза, т.е τ̂̕пр = τ̂пр , а если ∆˃∆кр , то данная гипотеза должна быть отклонена, как не обоснованная. Последний случай следует истолковывать следующим образом: имеющиеся статистические данные недостаточны для утверждения о наличии статистически значимых различий в оценках средней «наработки» на происшествие в каждой из двух групп объектов, отличающихся степенью внедрения мероприятий по предупреждению техногенных происшествий. Наибольший интерес представляет проверка рассматриваемых здесь статистических гипотез для решения задачи, связанной с выявлением аналитической зависимости между объемом N выборки исследуемых объектов и следующими параметрами: 1. Продолжительностью средней «наработки» на происшествие τпр =1/ωпр ; 2. Ожидаемым от принятых мер приростом этой величины ∆= τ̂̕пр –τ̂пр ; 3. Длительностью периода наблюдения за данной выборкой T; 4. Величиной ошибок 1-го и 2-го рода, возможных при принятии нулевой гипотезы ɑ и ß. Рассмотрим решение этой задачи статистического контроля, допустив, что количество тех исследуемых объектов, которые подвержены и не подвержены мероприятиям по предупреждению аварийности и травматизма, примерно одинаково. Следуя принятым допущениям, составим выражение для определения числа m происшествий на объектах, не подвергнутых мероприятиями по повышению безопасности. Его значение может быть рассчитано как математическое ожидание случайной величины, определяемое произведением общего количества соответствующих объектов (в данном случае — половина от их общего объема N) на вероятность возникновения там происшествий:
Что касается практической апробации описанной выше модели, то она осуществлена при оценке результативности ежегодных осмотров автотранспортных средств. В частности, была установлена несущественность вклада этих мероприятий в снижение числа дорожно-транспортных происшествий, что обусловлено многообразием факторов возникновения аварийности и травматизма на автотранспорте. Появление там происшествий зависит от большого числа причин: система предупреждения дорожно-транспортных происшествий в США и ЮАР, например, учитывает 85 таких факторов, состав которых напоминает выявленные ранее причины и факторы техногенных происшествий. Вот почему низкая эффективность рассматриваемого здесь мероприятия объясняется невысокой долей причин тех происшествий, которые обусловлены этим отдельно взятым фактором. Считается, что технические предпосылки составляют примерно 5 — 7%, что даже при малоправдоподобном допущении о полном их выявлении и устранении в результате техосмотра вряд ли существенно сократит количество автопроисшествий. И наконец, реальные «наработки» на происшествие измеряются годами, в частности, для одного автомобиля она оценивается обычно в 5 — 8 лет. Аналогичное состояние имеет место и при эксплуатации образцов другой техники. В этих условиях, для организации достоверного контроля эффективности мероприятий по предупреждению аварийности и травматизма, необходимо использовать либо очень большие выборки изучаемых объектов, либо осуществлять за ними наблюдение в течение продолжительного периода времени. Количественный анализ приведенных в них данных указывает, что для оценки эффективности сезонных техосмотров автотранспорта (при наработке на автопроисшествие тпр = 5,5 лет, допустимых ошибках а = р = 0,1 и реально ожидаемом приросте А = 1 мес), необходимо осуществить наблюдение за 1,27 миллиона автомобилями в течение полугода. Такие цифры объясняют и неудачи, связанные с попытками оценивать эффективность отдельных мероприятий по предупреждению аварийности и травматизма с помощью коэффициентов частоты Кч и тяжести Кт несчастных случаев с людьми. В порядке рекомендаций, вытекающих из приведенных здесь результатов моделирования и системного анализа, уместно предложить следующее. Использование методов статистического контроля более целесообразно проводить для оценки эффективности не отдельно внедряемых организационных или технических мероприятий, а их комплекса. Это обусловлено тем, что реализация совокупности подобных мер может сопровождаться значительным приростом во времени средней «наработки» на происшествие, что быстрее и легче зарегистрировать на практике. Таблица 2 - Фрагмент отчета с исходными данными и результатами
Заключение В заключение хотелось бы подчеркнуть необходимость внедрения в практику рассмотренных выше подходов к нормированию безопасности в техносфере. Как представляется, это будет способствовать улучшению управления процессом ее обеспечения за счет усовершенствования процедуры предъявления требований к разрабатываемым производственным процессам, более рационального использования ресурсов, повышения юридической и материальной ответственности за безусловное соблюдение предъявленных нормативов. Полученные здесь результаты подтверждают также необходимость и принципиальную возможность решения первой задачи программно-целевого планирования и управления совершенствованием безопасности. Подходы к решению других задач процесса обеспечения, контроля и поддержания заданных подобным образом показателей безопасности рассматриваются ниже.
Выводы по второй главе
В целом же приведенные сведения о порядке совершенствования управления безопасностью в техносфере на основе программно-целевого подхода могут интерпретироваться как преамбула к заключительному этапу трёхзвенной формулы преобразования действительности: «созерцание-мышление-практика». Рассмотрение последнего звена этой трёхзвенной формулы человеко-машинных и других сложноорганизованных систем как раз и является элементами математической теории организации.
3 Элементы математической теории организации
3.1 Модель организации как динамической системы
Анализ содержания изложенного выше подхода свидетельствует, что для решения рассматриваемой здесь проблемы необходимо не только повышение качества человеко-машинных систем, непосредственно занятых в производственных процессах, но и совершенствование всех сил и средств, предназначенных для обеспечения безопасности их функционирования. В совокупности все они образуют соответствующую систему (см. разд. 3.7), ядром которой служат специальные организации и подразделения. Такие формирования имеют иерархическую структуру и содержат, помимо коллективов людей, также приданные им материальные и финансовые ресурсы. Естественно, что для совершенствования всей такой системы или ее отдельных компонентов, решающих, например, задачи надзора и контроля за наиболее опасными технологическими объектами, должны быть использованы современные математические методы. Их внедрение в практику позволит оптимизировать характеристики этой организационной системы (ресурсы, связи, показатели) с помощью соответствующих алгоритмов. Охарактеризуем кратко отдельные положения математической теории организации [42], исходя из конструктивности этой теории и дефицита в отечественной литературе. В последующем под организацией, т. е. организационной системой, будем подразумевать некоторую, в общем случае человеко-машинную, систему, в которой существуют четкая координация и распределение обязанностей между всеми компонентами, направленные на достижение стоящей перед нею цели. Основным инструментарием изучения организаций в рамках теории организации является теория систем. Причины этого очевидны - признаки и свойства любой организации и любой системы, по сути, идентичны. К признакам системы относят: множество элементов, единство главной цели для всех элементов, наличие связей между ними, целостность и единство элементов, структура и иерархичность, относительная самостоятельность, четко выраженное управление. Основными свойствами любой системы принято считать: стремление сохранить свою структуру (основано на объективном законе организации - законе самосохранения); потребность в управлении (существует набор потребностей у человека, у животного, у общества, у стада животных, у большого социума); наличие сложной зависимости от свойств входящих в нее элементов и подсистем (система может обладать свойствами, не присущими ее элементам, и может не иметь свойств этих элементов). Каждая система имеет входное воздействие, технологию ее обработки, конечные результаты и обратную связь. Классификация систем может быть проведена по различным приз-накам. Основной является группировка по трем категориям: естественно-научной, технической и социально-экономической. В технических системах место и функции каждого механизма, узла и детали предопределены конструктором (технологом), который в процессе эксплуатации совершенствует ее. Техническая система включает оборудование и другие работоспособные изделия, имеющие инструкции для пользователя. Набор решений в технической подсистеме ограничен и последствия всех решений, как правило, предопределены. Решения носят строго формализованный характер и выполняются в строго определенном порядке. В естественных (биологических) системах место и функции каждого элемента, их взаимодействие и взаимосвязь предопределены природой, а совершенствование этой организации происходит по законам эволюции. Биологическая система включает флору и фауну планеты, в т.ч. человеческий организм. Набор решений также ограничен вследствие медленного эволюционного развития живых организмов. Последствия решений могут быть непредсказуемыми вследствие наличия субъективных факторов и огромного многообразия вариантов. В социально-экономических системах место, функции и взаимосвязь элементов предопределяются управляющим (менеджером), им же корректируются и поддерживаются. Социальная система характеризуется наличием человека как субъекта и объекта управления в совокупности взаимосвязанных элементов. Социальная система может включать биологическую и техническую подсистемы, а биологическая система - техническую подсистему. Математическая теория организации исследует свойства коллективов и групп на базе теории графов. Коллектив – сложная структура, сложная система, спектр всевозможных отношений, связей и взаимодействий его членов весьма широк. Обычно их сложно описать, анализировать и поэтому от большинства отношений абстрагируются и рассматривают часть отношений, поддающихся математической интерпретации. Концептуальная модель любой организации из системы обеспечения безопасности, например, федеральных комитетов Гостехнадзора и Энергонадзора, занятых контрольно-профилактической работой по предупреждению техногенных происшествий в техносфере, может интерпретироваться как динамическая система, представленная на рис. 3.1
Рис. 3.1.1. Модель организации как динамической системы
На вход этой системы, поступает множество входных воздействий X, а с ее выхода — результатов деятельности Y. Оператор же такой динамической системы Е{Т} осуществляет необходимые преобразования каждого входного элемента xk (свойства материального объекта или сообщения о нем) в выходной уl с некоторой результативностью Wkl, указывающей на эффективность конкретного преобразования, т.е. меру его полезности по отношению к затратам ресурса — средств и времени. Предполагается, что входные воздействия хк поступают с вероятностью Р(хк), а выходные — с условной вероятностью P(yi\xk). В этих условиях оператор Е{W}, иногда называемый организационной характеристикой и свидетельствующий о мере действенности или результативности организации на интервале Ах ее функционирования, будет определяться следующим выражением: E{W}=∑kl=WklP(xk)P(y1/xk) (3.1.1)
где {W} — матрица из элементов Wkl определяющих результативность отдельных преобразований конкретных входных элементов хk в выходные уl; к= 0,1, ..., m— номера элементов из множества входных воздействий; l= 1,2, ..., n — номера типов реакции (результатов работы) организации. Заметим, что величина к принимает нулевое значение, когда соответствующие входные воздействия отсутствуют на рассматриваемом интервале времени Дx (вход принимает значение х0, если, например, нет данных о происшествиях). Когда наблюдается равенство n=m, то матрица {W} — квадратная; тогда как при m<n считается, что отдельные входные сигналы дублируют избыточные r-е входные воздействия, а ряд элементов Wkl является одновременно функцией двух аргументов к и г, что записывается как W(k,r,l). Другими ограничениями на сомножители выражения (3.1.1) являются два условия: P(yl|xk)0 и ∑kl P(yl|xk)=1 (3.1.2)
свидетельствующие о работоспособности рассматриваемой динамической системы, например, той же инспекции Гостехнадзора или Энергонадзора. Одной из целей организации может быть обеспечение каждому входному воздействию хк таких преобразованных значений уl, которые соответствуют максимальной результативности Wkl=maxlWkl, или иначе:
W(k) = arg max Wkl
Последнее условие накладывает следующие требования на значения условных вероятностей преобразования:
P*(yl|xk)={1(для W*(k),если l=k) и 0 в других случаях}, (3.1.3)
обеспечивающие предельно высокую результативность организации:
E{W}=∑kl=WklP(xk)= ∑kWkkP(xk) (3.1.4)
Однако на практике не всегда возможно достижение идеальной результативности (2.4) на реальных промежутках времени Дх>0. Это обусловлено различной сложностью преобразований «вход—выход», предполагающей, что каждому из них необходимо свое время tkl >0 для обработки конкретного входа, допустим, анализа донесения о несчастном случае на производстве. Сумма таких времен будет определять общее время задержки, требуемое организации для преобразования всех входных сигналов и равное: Ј=∑kl tklP(x) P(yl|xk). (3.1.5)
Следовательно, соблюдение условий (2.3), (2.4) достигается лишь в маловероятном (практически невозможном) случае, когда имеет место строгое равенство Дх=J, поскольку при J >Дx будет происходить неограниченный рост времени задержки за счет накопления входных воздействий хк, а вероятность преобразований (3.1.2) при J<Дx окажется на практике величиной пренебрежимо малой, фактически равной нулю. С учетом приведенных соображений может быть сформулирована задача синтеза рассматриваемых организаций. Создаваемое подразделение Гостехнадзора, например, должно осуществлять такие преобразования входных воздействий хk поступающих с вероятностями Р(хк), которые максимизируют функционал Е{W} для всех J≤Д и Д≤ Дx. Иначе говоря, конструирование оптимальной структуры этой организации сводится к поиску таких Wkl и P(yl|xk), при которых обеспечивается экстремальное значение ее результирующей характеристики, в нашем случае — минимум ущерба от техногенных происшествий на подведомственных объектах за счет внедрения эффективных организационно-технических мероприятий. Приведенная содержательная постановка задачи требует большого объема исходной информации о входных, выходных и внутрисистемных параметрах рассматриваемой организации. Учитывая реальную сложность получения данных о законах распределения или других, исчерпывающих характеристиках, исследуемых случайных либо нечетко определенных величин, в ряде случаев надо отказаться от этих законов в пользу приближенного интервального оценивания их числовых характеристик, например, представляя их параметры нечеткими числами. Другими словами, в реальных условиях часто целесообразно вводить ограниченные с обеих сторон (снизу — «_» и сверху — «—») интервалы: [хк, xk]. Используемые интервалы неопределенности должны содержать внутри себя действительные значения неизвестных параметров, представления о которых должны изменяться по мере уточнения субъективных оценок опытными данными или расчетами, например, выполненными с помощью байесовских процедур. Функции п(х) принадлежности или плотности априорной f(Q|X) и апостериорной f(Q|,x-,X) вероятности могут иметь равномерно распределенный, треугольный или нормальный законы распределения.
3.2 Байесовская процедура уточнения интервала неопределенности
Идея повышения достоверности интервального оценивания (сокращения интервала неопределенности оцениваемых переменных), обеспечивающая с заданной доверительной вероятностью у «накрытие» их действительных значений, проиллюстрирована на рис. 3.2.1. Как следует из приведенной иллюстрации, значительное сужение интервала неопределенности достигается, например, при замене равномерного распределения, являющегося по своей природе распределением с максимальной энтропией, другим, более информативным в нашем случае — треугольным распределением. Это проявилось в уменьшении нового предела интегрирования [хj',хj']по сравнению с прежним [Xj,Xj], хотя каждый из соответствующих интервалов отсекает под своими плотностями f `(Q|X) и f(Q|X) одинаковую площадь, численно равную ў. В нижней части рисунка показана процедура объединения априорных представлений о распределении переменной X с вновь полученными данными x-, аппроксимированными функцией правдоподобия L(Q|x-). Такая процедура позволяет определять по формуле Т. Байеса апостериорную плотность f(Q|х-, X) распределения и сужать интервал [хj',хj']. Укажем, что интервальное оценивание факторов человеко-машинных систем может быть использовано для нормирования показателей безопасности и качества их функционирования, т.е. для выражения диапазона желаемого изменения этих выходных характеристик [L,U]: L≤E{W}<U, (3.2.1)
где L, U— соответственно нижнее (lower) и верхнее (upper) допустимые значения выходных характеристик конкретной организации. Заметим также, что при равенстве верхнего предела бесконечности, U = µ, двусторонний интервал изменения организационной характеристики вырождается в односторонний:
E{W}≥L, (3.2.2)
а в случае его неограниченного сокращения — стремления к некоторому фиксированному значению W* — он становится уже точечной оценкой, для которой справедливо условие:
Внутрисистемные характеристики конкретной организации, например, Wkl, P(yl|xk) и tkl, определяются надежностью персонала и используемой им техники, а также индивидуальными особенностями этих компонентов и связей между ними. С целью формализации всем таким компонентам присваивается имя — литерный или цифровой символ, а их свойства задаются набором соответствующих параметров. В качестве литерных символов персонала организации обычно используются прописные буквы латинского алфавита со следую щей их расшифровкой : А - Альфа (она), В - Браво (он), С - Чарли (он), D — Дельта (она), Е— Эхо (она)... Тогда как технические устройства принято кодировать уже римскими цифрами, текущие или предельные значения, которых в математических обозначениях могут подменяться строчными буквами латинского или греческого алфавитов. Индивидуальные же особенности членов персонала и технических элементов организации по степени значимости для результативности ее функционирования удобно делить на первостепенные (основные) и второстепенные (вспомогательные).
Рис. 3.2.1. Байесовская процедура уточнения интервала неопределенности
Основные свойства этих компонентов схожи с аналогичными свойствами всей организации, так как характеризуют ее эффективность (производительность), безошибочность и устойчивость, т.е. сопротивляемость изменениям. Эта группа свойств может характеризовать, например, насколько он, Браво, быстро осуществляет требуемые преобразования В роли же параметра, характеризующего безошибочность преобразований, чаще всего используют вероятности Prob(yl|xk)= P(yl|xk)=a или возможности Poss(yl|xk)= P(yl|xk)=b возникновения ошибок соответственно первого и второго рода. А вот для учета производительности и адаптивной гибкости применяется время tkl, необходимое для отдельного преобразования, перенастройки конкретного технического устройства или переключения человека с одних функциональных обязанностей на другие. В частности, адаптивная гибкость члена организации, допустим, Чарли, при переходе от преобразования kl к преобразованию rs реализуемых с вероятностями Р(хк), Рс(yl|xk) и Р(ur), Pc(us|ur), может быть оценена так:
или матрицей ||Rc||, состоящей из элементов,характеризующих сопротивляемость {
где Вспомогательные (второстепенные) свойства компонентов организации учитываются главным образом при описании членов ее персонала по тем признакам, которые отражают социальные аспекты людей и отличают их от робототехнических устройств. Не вдаваясь в подробности, заметим лишь, что чаще всего эти свойства характеризуют коллективистские начала человека (лояльность, совместимость целей, степень обособленности), а также механизмы его мотивации. Все второстепенные свойства обычно делят: а) на внутренние, определяемые миросозерцанием (мировоззрением и мироощущением) и самосознанием (самосознанием и самочувствием) личности; б) внешние, проявляемые реакцией человека, например, по отношению к использованию в организации привилегий, контроля и взысканий. В совокупности перечисленные свойства человека влияют на условия формирования отношений внутри организации, а посредством этого — и на ее характеристики. Поскольку вспомогательные свойства персонала как составной части организации имеют нечетко определенную природу, являясь, в сущности, лингвистическими переменными, то для их формализованного представления пригодны лишь соответствующие методы теории нечетких множеств. Продемонстрированные ранее возможности имитационного (логико-лингвистического) моделирования вселяют определенные надежды. Важное свойство личности и коллектива, как их стремление к сохранению гомеостазиса, оно порождено желанием биологических систем организовать взаимодействие с окружением с наименьшими издержками, поскольку это удерживает их характеристики на уровне, достаточном для длительного самосохранения. Именно в этом и заключается одна из причин консерватизма (сопротивляемости изменениям) людей и организаций, именно в этом объяснение потрясениям, вызванным революционными переходами рассматриваемых систем из одного устойчивого состояния в другое.
3.3 Математическая постановка иллюстративной задачи
Проиллюстрируем, как могут быть использованы изложенные здесь подходы для совершенствования работы, допустим, инспекции (отдела) Гостехнадзора или Энергонадзора. Известно, что эти управленческие организации занимаются контрольно-профилактической работой по исключению повторяемости техногенных происшествий на поднадзорных объектах, т. е. инспектированием, анализом состояния безопасности, разработкой мероприятий по устранению имеющихся там недостатков. Условимся также считать, что подведомственные объекты сгруппированы по конкретным признакам в определенные сочетания, на пример в К производственных объединений, а управляющему органу выделены некоторые ресурсы и задано их распределение между наиболее важными задачами. Математическая постановка задачи будет состоять в отыскании такого распределения обязанностей и времени между членами организации, при котором соблюдаются перечисленные требования и достигается максимум ее организационной характеристики:
где nj — количество поднадзорных объектов, имеющихся в j-м объединении; Ii, Ai, Ri —затраты времени управляющего органа на инспектирование, анализ и разработку контрольно-профилактических мероприятий на i-м объекте j-го объединения; a1, a2, a3 — нормативные показатели распределения этого времени между только что перечисленными задачами управляющего органа, Xj, Yj соответственно среднее количество техногенных происшествий и размерв1 среднего ущерба, зарегистрированные в j-й группировке и отнесенные к одному ее объекту; Т, b{0, 1} — резерв рабочего времени, выделенный управляющему органу для работы во всех производственных объединениях, и булева переменная. Анализ содержательной и математической постановок рассматриваемой здесь задачи оптимального синтеза показывает, что она относится к классу задач целочисленного программирования со смешанными (цело- и нецелочисленными) переменными. В результате ее решения по известным алгоритмам может быть найдено такое распределение {i,j} задач (целочисленные оптимизируемые параметры) и времени Тij (нецелочисленная переменная) управляющего органа, при котором обеспечивается максимальная результативность контрольно-профилактической работы на поднадзорных им объектах техносферы. В завершение знакомства с данной иллюстративной задачей отметим ее значительную вычислительную сложность, связанную с большой размерностью тех параметров, которые считаются существенно влияющими на управление процессом обеспечения техносферной безопасности. Это обстоятельство указывает не столько на потребность во всемерном упрощении подобных задач, сколько на необходимость их использования при их решении современных математических и машинных методов системного анализа и системного синтеза сложных систем. Вот почему, а также вследствие иллюстративности примера здесь не приводится описание алгоритма и результаты его решения.
Выводы по третьей главе
Таким образом, математическая теория организации исследует свойства коллективов и групп на базе теории графов. Коллектив – сложная структура, сложная система, спектр всевозможных отношений, связей и взаимодействий его членов весьма широк. Обычно их сложно описать, анализировать и поэтому от большинства отношений абстрагируются и рассматривают часть отношений, поддающихся математической интерпретации.
Заключение
В этой курсовой работе были рассмотрены вопросы моделирования и системного синтеза тех мероприятий, которые направлены на снижение техногенного риска. Фактически здесь продемонстрирована возможность реализаци на практике программно-целевого планирования и управления соответствующим процессом, выбранного в качестве основного метода обеспечения безопасности создаваемых техносфеных процессов и совершенствования уже существующих. Максимально возможное сокращение аварийности и травматизма на производстве и транспорте возможно лишь на основе программно-целевого подхода к изучению и решению этой проблемы.
Список использованных источников
1. Белов П.Г. Моделирование опасных процессов в техносфере. – М.: Изд-во АГЗ МЧС, 1999. – 124 с. 2. Введение в математическое моделирование / Под ред. П.В. Трусова. М.:Интермет инжиниринг, 2000. – 336 с. 3. Самарский А.А., Михайлов А.П. Математическое моделирование. Идеи. Методы. Примеры. – 2-е изд.М.:ФИЗМАТЛИТ, 2002. – 320 с. 4. Системный анализ и моделирование опасных процессов в техносфере: Учеб. Пособие для студ. высш. учеб. заведений/ П.Г. Белов. – М.: Издательский центр «Академия», 2003 – 512 с. ISBN 5-7695-1039-0 5. Хенли Д., Кумамото Х. Надежность технических систем и оценка риска: Пер.с англ. – М.: Машиностроение, 1984. – 528 с. 6. Хомяков Д.М., Хомяков П.М. Основы системного анализа – М.: Изд-во МГУ, 1996 – 108 с. 7. DrenickR. A mathematical organization theory. N.Y.: Acad.press, 1986.- 340 p.
|
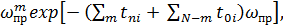(14)
и 
– соответственно суммарная «наработка» на происшествия объектов с зарегистрированными происшествиями и длительность функционирования всех остальных.
(15)
– средняя длительность времени функционирования одного объекта из числа той их части, где за время наблюдения были зарегистрированы техногенные происшествия;
– средняя продолжительность работы одного объекта из оставшейся группы.
, (17)
(18)
(3.2.3)
, (производительность), либо как хорошо оно, III компьютерное устройство, справляется со своими задачами 
, (безошибочность), или как легко она, Альфа, переключается с одной работы на другую 
(адаптивная гибкость).
(3.2.4)
} данного человека возможным модификациям. Затраты времени используются и для учета степени загруженности отдельных членов организации, в том числе и для руководства подчиненными и осуществления других функций. Например, если по своему служебному положению Ромео (он) обязан контролировать Джульетту (ее) и одновременно выполнять ка- кие-то другие управляющие воздействия (преобразовывать сигналы uk в ul), то его загруженность tr будет равна такой сумме:
(3.2.5)
— занятость руководителя отдела № 07 контролем деятельности подчиненного D.
;
;
;
;
;