 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Силы, действующие на шатунную шейку коленчатого вала.
Суммарная сила, действующая на шатунную шейку по радиусу кривошипа: РК = K +
где K = pк Fп = pк · 0,005685 · 103 кН.
Результирующая сила Rш. ш., действующая на шатунную шейку, подсчитывается графическим сложением векторов сил T и Рк , при построении полярной диаграммы. Масштаб сил на полярной диаграмме для суммарных сил Mр = 0,1 кН в мм.
Силы, действующие на колено вала.Суммарная сила, действующая на колено вала по радиусу кривошипа:
Результирующая сила, действующая на колено вала Rк = Rш.ш. + KRk определяется по диаграмме Rш.ш
Таблица 1.12
1.12. УРАВНОВЕШИВАНИЕ ДВИГАТЕЛЯ
Центробежные силы инерции рассчитываемого двигателя и их моменты полностью уравновешены: ΣKR =0; ΣМR = 0. Силы инерции первого порядка и их моменты также уравновешенны: ΣРjI = 0; Σ МR = 0. Уравновешивание сил инерции второго порядка в рассчитываемом двигателе нецелесообразно, ибо применение двухвальной системы с противовесами значительно усложнят конструкцию двигателя. Полученные расчётным путём параметры карбюраторного двигателя близки по значениям прототипу, т.е. можно сделать вывод, что проект выполнен верно и параметры двигателя не требуют корректировки.
РАСЧЁТ ОСНОВНЫХ ДЕТАЛЕЙ ДВИГАТЕЛЯ
2.1. РАСЧЁТ ПОРШНЕВОЙ ГРУППЫ КАРБЮРАТОРНОГО ДВИГАТЕЛЯ
Поршень является наиболее напряжённым элементом поршневой группы, воспринимающий высокие газовые, инерционные и тепловые нагрузки. Его основными функциями являются уплотнение внутрицилиндрового пространства и передача газовых сил давления с наименьшими потерями кривошипно-шатунному механизму.
Рис. 2.1. Схема поршня Рис. 2.2. Изменение температуры по высоте поршня и зазоров между поршнем и зеркалом цилиндра в разных сечениях На основании данных расчётов получили: диаметр цилиндра D = 85 мм; ход поршня S = 78 мм; действительное максимальное давление сгорания Pд = 6,8288 МПа; при nN = 3200 об/мин; площадь поршня Fп = 56,85 мм2; наибольшую нормальную силу Nmax = MH, при φ = ; массу поршневой группы mn = 0,4776 кг; λ = 0,285. В соответствии с существующими аналогичными двигателями и с учётом соотношений принимаем: толщину днища поршня δ = 7,5; высоту поршня Н = 88 мм; высоту юбки поршня hю = 58 мм; радиальную толщину кольца t = 3,5 мм; радиальный зазор кольца в канавке поршня Δt = 0,8 мм; толщину стенки головки поршня s = 5 мм; число и диаметр масляных каналов в поршне n′п = 10 и dм = 1 мм; (см. рис. 2.1). Материал поршня – эвтектический алюминиевый сплав с содержанием кремния около 12 %, ап = 22·10-6 1/К; материал гильзы цилиндра – серый чугун, ац = 11·10-6 1/К. Напряжение изгиба в днище поршня
σиз = pzd (ri /δ) = 6,8288(33,2/7,5) = 30,23 МПа,
где ri = D/2 – (s +t +Δt) = 85/2 – (5 +3,5 +0,8) = 33,2 мм.
Напряжение сжатия в сечении х–х σсж = Pzd /Fx-x = 0,0388/0,000828 = 46,86 МПа,
где Pzd = pzd ∙Fп = 6,8288 ∙ 56,85 ∙ 10-6 = 0,0388 MH; Fx-x = dx = D – 2(t +Δt) = 85 – 2 ⋅ (3,5 +0,8) = 76,4 мм;
F’ = (dx – di) dm / 2 = 3,8 мм2. Напряжение разрыва в сечении х–х : Максимальная угловая скорость холостого хода
ωx.x.max = πnx.x.max / 30 = 3,14 ⋅ 3200 / 30 = 334,93 рад/с.
Масса головки поршня с кольцами, расположенными выше сечения х–х: mx-x = 0,5mп = 0,5 ⋅ 0,4776 = 0,2388 кг.
Максимальная разрывающая сила Pj = mx-x ∙ R ∙ ω2x.x.max ∙ (1 + = 0,2388 ∙ 0,039 ∙ 334,932 ∙ (1 + 0,285) ∙ 10-6 = 0,00134 МПа.
Напряжение разрыва
σP = Рj / Fx-x = 0,00134 / 0,000828 = 1,618 МПа.
Напряжения в верхней кольцевой перемычке: – среза
τ = 0,0314pzd D / hц = 0,0314 ⋅ 6,8288 ⋅ 85/3,5 = 5,207 МПа;
– изгиба
σиз = 0,0045pzd (D / hц)2 = 0,0045 ⋅ 6,8288 ⋅ (85/3,5)2 = 18,125 МПа;
– сложное
Удельное давление поршня на стенку цилиндра: q1 = 0,0044 / (0,58 ⋅ 0,085) = 0,925 МПа; q2 = 0,0044 / (0,088 ⋅ 0,085) = 0,610 МПа.
Ускорение приработки юбки поршня, а также уменьшение трения и снижения износа пары – юбка поршня – стенка цилиндра – достигается покрытием юбки поршня тонким слоем олова, свинца или оловянно-свинцового сплава. Гарантированная подвижность поршня в цилиндре достигается за счёт установления диаметральных зазоров между цилиндром и поршнем при их неодинаковом расширении в верхнем сечении головки поршня Диаметры головки и юбки поршня с учётом монтажных зазоров: Dг = D – Δг = 85 – 0,574 = 84,43 мм; Δг = 0,007D = 0,007 ⋅ 85 = 0,595 мм; Dю = D – Δю = 85 – 0,164 = 84,84 мм; Δю = 0,002D = 0,002 ∙ 85 = 0,17 мм.
Диаметральные зазоры в горячем состоянии:
= 85(1 + 11 ∙ 10-6 ∙ (383 – 293)) – 84,43 ∙ (1 + 22 ∙ 10-6 ∙ (593 – 293)) = 0,097 мм;
= 85(1 + 11 ∙ 10-6 ∙(383 – 293)) – 84,84(1 + 22 ∙ 10-6 ∙ (413 – 293)) = 0,02 мм.
где Тц = 383 К, Тг= 593 К, Тю = 413 К приняты с учётом жидкостного охлаждения двигателя.
2.1.1. РАСЧЁТ ПОРШНЕВЫХ КОЛЕЦ БЕНЗИНОВОГО ДВИГАТЕЛЯ
Материал кольца – серый легированный чугун, Е = 1,2 ⋅ 105 МПа. Среднее давление кольца на стенку цилиндра
где A0 = 3t = 3·3,5 = 10,5 мм.
Давление кольца на стенку цилиндра в различных точках окружности определяется по формуле
p = pср ∙ μк ,
Напряжение изгиба кольца в рабочем состоянии
Напряжение изгиба при надевании кольца на поршень
Монтажный зазор в замке поршневого кольца
Δк = Δ′к + πD [αк (Tк –T0 )− αц (Tц –T0 )]= = 0,08 + 3,14 ∙ 85 ∙ (11 ∙ 10-6 ∙ (493 – 293) – 11 ∙ 10-6 ∙ (383 – 293)) = 0,403 мм.
2.1.2. РАСЧЁТ ПОРШНЕВОГО ПАЛЬЦА КАРБЮРАТОРНОГО ДВИГАТЕЛЯ
Принимаем: действительное максимальное давление сгорания рmax = pzd = 6,8288 МПа при оборотах 3200 мин-1 (из расчёта скоростной характеристики), наружный диаметр пальца dп = 22 мм, внутренний диаметр пальца dв = 15мм, длина пальца lп = 68 мм, длина втулки шатуна lш = 28 мм, расстояние между торцами бобышек b = 32 мм. Материал поршневого пальца – сталь 15Х, Е = 2·105 МПа. Палец плавающего типа. Расчётная сила, действующая на поршневой палец: – газовая
– инерционная
= − 0,4776 ∙ 3352 ∙ 0,039 ∙ (1 + 0,285) ∙ 10-6 = − 0,0026861 МН
где ωм = πnм /30 = 335 рад/с;
– расчётная P = Pz max + k ∙ Pj = 0,0388 − 0,82 ⋅ 0,00134 = 0,037701 МН.
Удельное давление пальца на втулку поршневой головки шатуна
Удельное давление пальца на бобышки
Напряжение изгиба в среднем сечении пальца при условии распределения нагрузки по длине кольца, согласно эпюре, приведено на рисунке:
где α = dв /dп = 15/22 = 0,682
Касательные напряжения среза в сечениях между бобышками и головкой щатуна
Наибольшее увеличение горизонтального диаметра пальца при овализации
Напряжения овализации на внешней поверхности пальца – в горизонтальной плоскости (точки 1, ψ = 0º)
– в вертикальной плоскости (точки 3, ψ = 90º)
Напряжение овализма на внутренней поверхности пальца: – в горизонтальной плоскости (точки 2, ψ = 0º)
– в вертикальной плоскости (точки 4, ψ = 90º)
Список используемой литературы 1. Колчин А. И., Демидов В. П. «Расчёт автомобильных и тракторных двигателей».- М.: Высшая школа, 2008 2. Николаенко А. В. «Теория, конструкция и расчёт автотракторных двигателей».- М.: Колос, 1984 3. Мелисаров В. М., Беспалько П. П., Каменская М. А. «Тепловой расчёт и тепловой баланс карбюраторного двигателя и двигателя с впрыском топлива».- Т.: ТГТУ, 2009.
|
= (K – 4,4937), кН,
кН
0,785 ∙ (76,42 – 68,82) – 10 ∙ 3,8 = 0,000828 м2
= 85 – 2(5 + 3,5) + 0,8 = 68,8 мм;
) ∙ 10-6 =
МПа.
и нижнем сечении юбки 
.
МПа
МПа
МПа
6,8288 ∙ 0,005685 = 0,0388 МПа;
МПа;
МПа.
МПа
МПа
мм
МПа
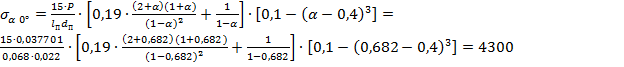МПа
МПа
МПа.