 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Для определения минимальной длины шатуна
Построив кинематическую схему кривошипно-шатунного механизма (см. рис. 1.5), устанавливаем, что ранее принятые значения Lш и λ обеспечивают движение шатуна без задевания за нижнюю кромку цилиндра. Следовательно, перерасчёта величин Lш и λ не требуется. Перемещение поршня. Определяем перемещение поршня в зависимости от угла поворота коленчатого вала двигателя
Расчёт
Значения для
Рис. 1.6. Путь, скорость и ускорение поршня карбюраторного двигателя
Угловая скорость вращения коленчатого вала
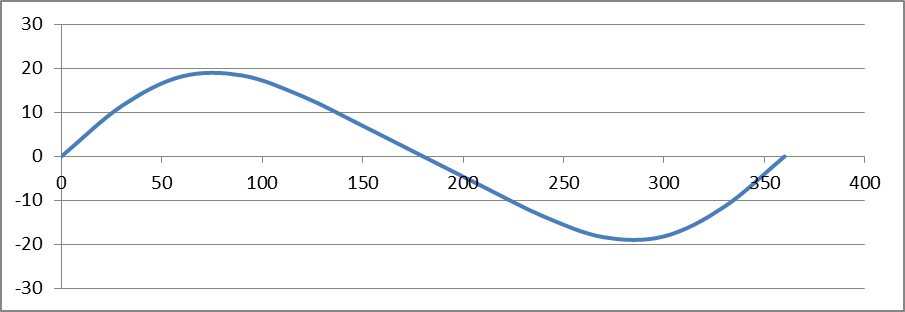
Скорость поршня. Учитывая, что при перемещении поршня скорость его движения переменна и зависит только от изменения угла поворота кривошипа и отношения λ/2, тогда
Значения для [sin Ускорение поршня рассчитывается по формуле
Значения для (cos По данным табл. 1.9. построены графики рис. 1.5 sx в масштабе Ms = 2 мм в мм, vn – в масштабе Мv = 1 м/с в мм, j – в масштабе Mj = 500 м/с2 в мм. Масштаб угла поворота коленчатого вала При j = 0 vп = ±vmax , а на кривой sx – эта точка перегиба.
1.11. РАСЧЁТ ДИНАМИКИ КАРБЮРАТОРНОГО ДВИГАТЕЛЯ Силы давления газов.Индикаторную диаграмму (см. рис 1.4), полученную в тепловом расчёте, развертывают по углу поворота кривошипа (рис 1.7) по методу Брикса. Поправка Брикса Rλ /(2Ms ) = 39 ⋅ 0,285 /(2 ⋅1) = 5,56 мм,
где Мs – масштаб хода поршня на индикаторной диаграмме. Масштабы развернутой диаграммы: давлений и удельных сил Mp = 0,05 МПа в мм; полных сил Mp = Mp ∙ Fn = 0,05 · 0,004776 = 0,000239 МН в мм, или Мp = 239 H в мм, угла поворота кривошипа Мp = 3° в мм, или
где ОВ – длина развёрнутой индикаторной диаграммы, мм. По развёрнутой диаграмме через каждые 10° угла поворота кривошипа определяют значения Dpr и заносят в гр. 2 сводной табл. 1.10 динамического расчёта (в таблице значения даны через 30° и точка при φ = 370°).
Таблица 1.10
Приведение масс частей кривошипно-шатунного механизма.
Масса поршневой группы (для поршня из алюминиевого сплава принято (т'п = 100 кг/м2)
Масса шатуна (для стального кованого шатуна принято т'ш = 150 кг/м2)
Масса неуравновешенных частей одного колена вала без противовесов (для литого чугунного вала принято m'к = 140 кг/м2)
Масса шатуна, сосредоточенная на оси поршневого пальца
Масса шатуна, сосредоточенная на оси кривошипа
Массы, совершающие возвратно-поступательное движение
Массы совершающие вращательные движение
Удельные и полные силы инерции.Из табл. 1.9. переносят значения j в гр. 3 табл. 1.10 и определяют значения удельной силы инерции возвратно-поступательно движущихся масс (гр. 4):
центробежная сила инерции вращающихся масс
центробежная сила инерции вращающихся масс шатуна
центробежная сила инерции вращающихся масс кривошипа
Удельные суммарные силы.Удельная сила (МПа), сосредоточенная на оси поршневого пальца (гр. 5, табл. 1.10):
Удельная нормальная сила (МПа) pN = ptgβ. Значения tgβ определяют для λ = 0,285 по табл. 1.12 и заносят в гр. 6, а значения рN – в гр. 7 (табл. 10). Удельная сила (МПа), действующая вдоль шатуна (гр. 9): Ps = p (1/cosβ).
Удельная сила (МПа), действующая по радиусу кривошипа (гр. 11): pк = pcos(φ + β) / cosβ.
Удельная (гр. 13) и полная (гр. 14) тангенциальные силы (МПа и кН): pT = psin(φ + β) / cosβ и T = pT Fп = pT 0,005685 ⋅103.
По данным табл. 1.10 строят графики изменения удельных сил pj, p, ps, pN, pк и pT в зависимости от изменения угла поворота коленчатого вала φ рис. 1.7. Среднее значение тангенциальной силы за цикл:
Крутящие моменты.Крутящий момент одного цилиндра (гр. 15)
Mкр. ц. = TR = T ⋅0,039⋅103 Н·м.
Период изменения крутящего момента четырёхтактного двигателя с равными интервалами между вспышками
θ = 720/ i = 720/ 4 = 180° .
Суммирование значений крутящих моментов всех четырёх цилиндров двигателя осуществляется табличным методом в масштабе Мм – 10 Н·м в мм. Средний крутящий момент двигателя: по данным теплового расчёта
Таблица 1.11
|
мм.
производится аналитически через каждые 10° угла поворота коленчатого вала.
при различных 
взяты из табл. 1.6 как средние между значениями при λ = 0,28 и 0,29 и занесены в гр. 2 расчётной табл. 1.9 (для сокращения объёма значения в таблице даны через 30◦).
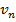, м/с
◦
= πn / 30 = 3,14 ⋅ 4500 / 30 = 471 рад/с.
м/с.
– в гр. 5 табл. 1.9.
м/с2.
= 3° в мм.
рад в мм,
°
100 
0,004776 = 0,4776 кг.
150 ∙ 0,004776 = 0,7164 кг.
140 ∙ 0,004776 = 0,66864 кг.
0,275 ∙ 0,7164 = 0,19701 кг.
0,725 ∙ 0,7164 = 0,51939 кг.
0,4776 + 0,19701 = 0,67461 кг.
0,66864 + 0,51939 = 1,18803 кг.
МПа;
− 1,18803 ∙ 0,039 ∙ 4712 ∙ 10-3 = − 10,2786 кН;
− 0,51939 ∙ 0,039 ∙ 4712 ∙ 10-3 = − 4,4937 кН;
− 0,66864 ∙ 0,039 ∙ 4712 ∙ 10-3 = − 5,7849 кН.
Н.
Н∙м
, Н∙м
, Н∙м