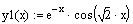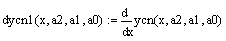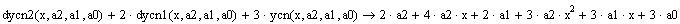 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Лабораторная работа: Дифференциальные уравнения
Задача 1. Найти решение уравнения с разделенными переменными ydy=(exp(x)/1+exp(x))dx, удовлетворяющее начальному условию y(0)=1 (задача Коши). Изобразите график решения (интегральную кривую, проходящую через точку (0,1)). Решение: 1) Установите режим автоматических вычислений. 2) Установите режим отображения результатов символьных вычислений по горизонтали, установив метку Horizontaly в окне диалога строки Evaluation Style меню Symbolics. 3) Введите начальные условия y(x0)=y0:
4) Если уравнение имеет вид Y(y)dy=X(x)dx, определите подынтегральные функции Y(y) и X(x):
5) Вычислите символьно интегралы с переменными верхними пределами и нижними пределами, равными начальным условиям x0 и y0:
6) Запишите уравнение , задающее неявно y(x) как функцию x, и решите его символьно относительно переменной y:
7) Выбираете решение, удовлетворяющее условию y(0)=1, и определите как функцию переменной x:
8) Постройте график найденного решения:
Задача 2. Решите на отрезке [0,3] задачу Коши y'=sin(xy), y(0)=1 методом Рунге-Кутты с постоянным шагом на сетке из 20 (40, 100) равнооотстоящих узлов. Решение: 1) Установите режим автоматических вычислений. 2) Присвойте переменной ORIGIN значение, равное 1:
3) Присвойте начальное значение решения переменной y1:
4) Определите правую часть уравнения f(x,y):
5) Вычислите решение, используя функцию rkfixed(y,x1,x2,npoints,f), где у - вектор начальных условий, х1 и х2 - концы отрезка интегрирования, npoints- число узлов на отрезке интегрирования, f - правая часть уравнения. В результате получите матрицу размерности (npoints, 2), в первом столбце которой содержатся значения х, во втором - значения у.
6) Постройте на одном графике найденные решения:
Задача 3. Решите на отрезке [0,3] задачу Коши у"=ехр(-ху), у(0)=1, у'(0)=1 методом Рунге-Кутты с постоянным шагом на сетке из 20 (40 , 100) равноотстоящих узлов. Решение: Сведите решение задачи для уравнения к задаче для системы. Обозначьте у1(х)=у(х) и у2(х)=у'(х). Поскольку у"(х)=(у'(x))'=y2'(x), то получим у1'=y2 y1(0)=1 y2'=exp(-xy1) y2(0)=1 1) Установите режим автоматических вычислений. 2) Присвойте переменной ORIGIN значение, равное 1:
3) Присвойте начальное значение решения вектору-столбцу с именем у:
4) Определите правую часть уравнения, присвойте соответствующие выражения элементам вектора-столбца с именем f(x,y):
5) Вычислите решение, используя функцию rkfixed:
6) Постройте на одном графике найденные решения:
Задача 4. Найдите общее решение однородного уравнения y''+2y'+3y=0. Решите задачу Коши с начальными условиями у(0)=1, y'(0)=1. Проверьте правильность решения. Изобразите его график. Решение: 1) Установите режим автоматических вычислений. 2) Присвойте переменной ORIGIN значение, равное 1:
3) Запишите характеристический многочлен уравнения и найдите его корни:
4) Если характеристическое уравнение имеет 2 различных действительных корня l 1 и l 2, то фундаментальная система решений имеет вид Запишите функции фундаментальной системы решений:
5) Запишите общее решение уравнения (как функцию переменных х, с1 и с2):
6) Найдите значения констант с1 и с2, при которых выполняются заданные начальные условия у(0)=1 и у'(0)=1:
7) Запишите решение задачи Коши:
8) Проверьте решение подстановкой в уравнение:
9) Проверьте выполнение начальных условий:
10) Постройте график решения:
11) Решите задачу Коши методом Рунге-Кутты и постройте график приближенного решения:
12) Сравните графики.
Задача 5. Найдите общее решение неоднородного уравнения y''+2y'+3y=x*x+1. Проверьте правильность решения. Решение: Общее решение линейного неоднородного уравнения записывается как сумма общего решения однородного уравнения и любого частного решения неоднородного уравнения. 1) Установите режим автоматических вычислений. 2) Присвойте переменной ORIGIN значение, равное 1:
3) Найдите общее решение однородного уравнения у"+2y'+3y=0:
4) Запишите выражение для частного решения как функцию переменной х и неизвестных коэффициентов. Вид частного решения устанавливается по виду правой части уравнения.
5) Подставьте выражение частного решения в левую часть уравнения:
6) В полученном выражении приведите подобные отностительно степеней х, для чего выделите переменную х и щелкните по строке Collect в меню Symbolics:
7) Приравняв коэффициенты при степенях х полученного выражения левой части уравнения и выражения правой части, запишите и решите систему относительно параметров а1, а2, а0:
8) Запишите частное решение с найденными коэффициентами а2,а1,а0:
9) Запишите общее решение:
10) Проверьте решение подстановкой:
[1] По материалам: Контур управления: Книга 2: Учебное пособие/Пер. с англ. - Жуковский: МИМ ЛИНК, 2005. – 82 с.: рис., табл., диагр. – («Менеджер и организация»). [2] По материалам: Плотинский Ю.М. Модели социальных процессов: Учебное пособие для высших учебных заведений. – Изд. 2-е, перераб. и доп. – M.: Логос, 2001. – 296 с.: ил. [3] Адаптировано по материалам сайта www.exponenta.ru |
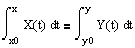
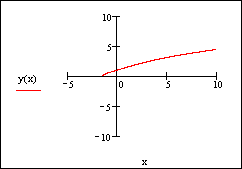
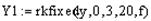
и 
. Если характеристическое уравнение имеет 2 равных действительных корня l 1=l 2=l , то фундаментальная система решений имеет вид 
. Если характеристическое уравнение имеет 2 комплексных корня l 1=a +ib и l 2=a -ib , то фундаментальная система решений имеет вид 
и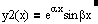 
.
