 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Пикетов и плюсовых точек по карте
Цель работы:Получить навыки выбора радиусов кривых в плане, расчета элементов прямых и кривых, составления ведомости прямых и кривых. Научиться определять высоты пикетов и плюсовых точек по карте. Оборудование:микрокалькулятор, миллиметровая линейка, масштабная линейка, циркуль-измеритель, циркуль, геодезический транспортир.
Проектирование плана трассы. Составление ведомости прямых и кривых При движении транспортные средства не могут резко изменить направление движения, причем, чем выше скорость движения, тем сложнее изменить его направление, а поэтому для обеспечения удобного и безопасного движения транспортных средств на участках изменения направления устраивают кривые, которые обеспечивают постепенное изменение направления без снижения скорости или с незначительным снижением последней. Кривая вписывается во внутренний угол ломаной трассы смежный с углом поворота, таким образом, чтобы лучи, образующие данный угол были касательными к кривой (рис. 3.1). Точки, в которых кривая касается лучей внутреннего угла ломаной трассы, называются: начало кривой (НК) и конец кривой (КК), а расстояния от НК до ВУ от ВУ до КК называются тангенсами и обозначаются
Рис. 3.1 Вписывание кривых в ломаную дорожной трассы
Кривая дорожной трассы, может быть, простой в виде дуги окружности с радиусом Радиусы кривых должны назначаться в нормальных условиях не менее 1000 м. Если размещение кривой с радиусом 1000 м и более не возможно, то допускается применение радиусов величиной до 1000 м, но не менее указанных в табл. 51 СНиП 2.05.07-91*. Во всех случаях следует назначить стандартные значения радиусов кривых (м): 5000; 4000; 3000; 2500; 2000; 1500; 1000; 800; 700; 600; 500; 400; 300; 250; 200; 150; 125; 100; 60; 30; 25; 20; 15. Радиус кривой в плане обосновывают исходя из возможности размещения смежных кривых и устройства между ними прямой вставки, или переходных кривых, ограничения длин прямых вставок (максимальная длина прямой вставки – 1500 м). Следует учитывать, что пересечение существующих дорог, водотоков, лощин более рационально осуществлять прямыми участками (прямыми вставками). Зная расстояние между вершинами углов поворота Простая кривая, представляющая собой дугу окружности с радиусом а) тангенс
б) кривая (длина кривой)
в) биссектриса – расстояние от ВУ до середины кривой
Рис. 3.2 Простая кривая (дуга окружности)
СНиП 2.05.02-85* рекомендует на дорогах общего пользования при
где Каждая переходная кривая обеспечивает поворот на угол
Рис. 3.3 Сложная симметричная кривая (две клотоиды одинаковой длины и дуга окружности)
Круговая кривая обеспечивает поворот на угол Тангенс симметричной кривой равен
где
где
Длина симметричной кривой (кривая)
Биссектриса симметричной кривой
В случае, когда клотоиды, примыкающие с обеих сторон к основной кривой имеют разные длины
Тангенсы
В формулах (3.12)
Рис. 3.4 Сложная несимметричная кривая (две клотоиды разной длины и дуга окружности) Длина несимметричной кривой
При устройстве кривой длина трассы сокращается на величину домера
Трасса делится на участки длиной 100 м, которые называются пикетами и на участки длиной 1000 м, которые называются километры, десять пикетов образуют километр. Положение точек трассы определяют в пикетажном выражении вида ПК Положение НК и КК при разбивке кривой устанавливают путем отмера тангенсов от ВУ в соответствующую сторону: для установления НК к НТ, а КК – к КТ. Пикетажное положение НК и КК определяют по зависимостям: НК=ВУ– где ВУ – пикетажное положение вершины угла поворота. Пикетажное положение начала основной кривой (НОК) и конца основной кривой (КОК) соответственно равно: НОК=НК+ Пикетажное положение ВУ определяется по формулам: ВУ1= Пикетажное положение КТ равно КТ= ВУ Длина прямой вставки
где НК1, НК КК Детальная разбивка кривых и вынос пикетов на кривые производятся от НК и КК, при этом удобно использовать способ прямоугольных координат. Начало координат совмещается с НК или КК, ось абсцисс направляется по тангенсу к ВУ, ось ординат перпендикулярно оси абсцисс в сторону центра кривой. Задаваясь текущей координатой положения точки на кривой
Если кривая сложная, то в пределах клотоиды (
В пределах основной кривой, когда
В формулах (3.20), (3.21) и (3.22) все угловые параметры измеряются в рад. Все количественные характеристики элементов плана трассы заносят в ведомость прямых и кривых (табл. 3.1). В данной ведомости после строки, соответствующей КТ записывают суммы: углов поворота правых
Пример оформления плана трассы показан на рис. 3.5.
М 1:10000 Рис. 3.5 План трассы |



 ,
,  (рис. 3.1).
(рис. 3.1).
 или сложной, образованной двумя переходными кривыми и дугой окружности с радиусом
или сложной, образованной двумя переходными кривыми и дугой окружности с радиусом  , на протяжении которой радиус
, на протяжении которой радиус  постепенно уменьшается от
постепенно уменьшается от  в точке касания к прямому участку до радиуса основной кривой
в точке касания к прямому участку до радиуса основной кривой  , расстояния от вершин до пересекаемых объектов (дорог, водотоков) можно выбрать величину радиуса
, расстояния от вершин до пересекаемых объектов (дорог, водотоков) можно выбрать величину радиуса  /tg
/tg  , где
, где  – расстояние от ВУ до пересекаемого объекта, если на участке между двумя ВУ нет объектов, которые следует пересечь прямой вставкой, то радиусы смежных кривых выбирают исходя из возможности размещения кривых и устройства между ними прямой вставки длиной
– расстояние от ВУ до пересекаемого объекта, если на участке между двумя ВУ нет объектов, которые следует пересечь прямой вставкой, то радиусы смежных кривых выбирают исходя из возможности размещения кривых и устройства между ними прямой вставки длиной  , в этом случае
, в этом случае  , где
, где  ,
,  – соответственно тангенсы круговых кривых, устраиваемых в ВУ
– соответственно тангенсы круговых кривых, устраиваемых в ВУ  и ВУ
и ВУ  и определяемые по формуле (3.1), м.
и определяемые по формуле (3.1), м.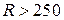 м, а на подъездных дорогах при
м, а на подъездных дорогах при  м. Данная кривая показана на рис. 3.2, она характеризуется следующими параметрами:
м. Данная кривая показана на рис. 3.2, она характеризуется следующими параметрами:
 tg
tg 
 ; (3.2)
; (3.2)
 . (3.3)
. (3.3)
 не более допускаемой, то есть принимаемая длина клотоиды
не более допускаемой, то есть принимаемая длина клотоиды  , (3.4)
, (3.4) – параметр клотоиды, м.
– параметр клотоиды, м. (град.), равный
(град.), равный arctg
arctg  ;
;  ;
;  . (3.5)
. (3.5)
 , а разбивка кривой с переходными кривыми длиной
, а разбивка кривой с переходными кривыми длиной  . При
. При 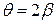 кривая состоит из двух клотоид и называется биклотоидой.
кривая состоит из двух клотоид и называется биклотоидой. ;
;  , (3.6)
, (3.6) – абсцисса конца клотоиды (длина ортогональной проекции клотоиды на тангенс), м;
– абсцисса конца клотоиды (длина ортогональной проекции клотоиды на тангенс), м; – сдвижка основной кривой, образованная переходными кривыми, м.
– сдвижка основной кривой, образованная переходными кривыми, м. , (3.7)
, (3.7) – ордината конца клотоиды, м.
– ордината конца клотоиды, м. . (3.8)
. (3.8)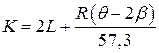 . (3.9)
. (3.9) . (3.10)
. (3.10) и
и  , кривая будет несимметричной, она имеет разные тангенсы
, кривая будет несимметричной, она имеет разные тангенсы  и
и  , а условие разбивки кривой с такими клотоидами будет
, а условие разбивки кривой с такими клотоидами будет  . Углы
. Углы  и
и  , они рассчитываются по формулам (3.7) и (3.8) в зависимости от
, они рассчитываются по формулам (3.7) и (3.8) в зависимости от  , равную
, равную . (3.11)
. (3.11) ;
;  . (3.12)
. (3.12) и
и  определяются по формуле (3.6) в зависимости от
определяются по формуле (3.6) в зависимости от 
 . (3.13)
. (3.13) равного
равного ;
;  . (3.14)
. (3.14) , где
, где  – номер пикета на котором расположена точка;
– номер пикета на котором расположена точка;  – расстояние от начала данного пикета до рассматриваемой точки, м. Положение точек трассы можно задавать в километровом выражении вида км
– расстояние от начала данного пикета до рассматриваемой точки, м. Положение точек трассы можно задавать в километровом выражении вида км 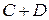 , где
, где  – расстояние от начала данного километра до рассматриваемой точки, м. Пикеты и километры разбивают от НТ начиная с нулевого (ПК 0; км 0). После каждой вершины угла поворота откладывают величину домера, рассчитанную в зависимости от параметров кривой, вписываемой в данный угол, которая не учитывается при разбивке пикетов, то есть остаток длины пикета после ВУ откладывается больше своей длины на величину домера (например, если ВУ имеет пикетажное положение ПК 25+35,82, то после ВУ до ПК 26 необходимо отложить расстояние, равное 100–35,82=64,18 м, но так как после устройства кривой длина трассы сократится на
– расстояние от начала данного километра до рассматриваемой точки, м. Пикеты и километры разбивают от НТ начиная с нулевого (ПК 0; км 0). После каждой вершины угла поворота откладывают величину домера, рассчитанную в зависимости от параметров кривой, вписываемой в данный угол, которая не учитывается при разбивке пикетов, то есть остаток длины пикета после ВУ откладывается больше своей длины на величину домера (например, если ВУ имеет пикетажное положение ПК 25+35,82, то после ВУ до ПК 26 необходимо отложить расстояние, равное 100–35,82=64,18 м, но так как после устройства кривой длина трассы сократится на  ).
).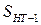 ; ВУ
; ВУ  –
–  ; ВУ
; ВУ  =ВУ
=ВУ  +
+  –
–  . (3.17)
. (3.17) –
– 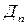 . (3.18)
. (3.18) равна
равна =НК1;
=НК1;  =НК
=НК  =КТ–КК
=КТ–КК  , которая представляет собой расстояние по кривой от НК или КК до рассматриваемой точки (м), вычисляют прямоугольные координаты
, которая представляет собой расстояние по кривой от НК или КК до рассматриваемой точки (м), вычисляют прямоугольные координаты  и
и  этой точки в принятой системе координат. Если кривая состоит только из дуги окружности, то
этой точки в принятой системе координат. Если кривая состоит только из дуги окружности, то ;
;  . (3.20)
. (3.20) ) координаты будут равны
) координаты будут равны ;
;  . (3.21)
. (3.21)
 ;
;  . (3.22)
. (3.22) и левых
и левых  (
(  – количество правых углов поворота из общего числа углов поворота
– количество правых углов поворота из общего числа углов поворота  (
(  – тангенсы
– тангенсы  -ой несимметричной кривой, если кривая симметричная, то
-ой несимметричной кривой, если кривая симметричная, то  ), кривых
), кривых  , домеров
, домеров 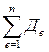 , прямых вставок
, прямых вставок  (
(  – количество прямых вставок), расстояний между вершинами углов и выполняют проверку результатов расчета параметров трассы исходя из следующих требований:
– количество прямых вставок), расстояний между вершинами углов и выполняют проверку результатов расчета параметров трассы исходя из следующих требований: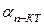 –
–  =
=  ;
;  ;
; КТ. (3.23)
КТ. (3.23)