ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Исходные данные по нагрузке и размерам
В табл. 17 приняты следующие обозначения: А, В – расстояние от начала координат до точки приложения соответственно момента или сосредоточенной силы; С2, С3 – расстояние от начала координат до начала действия равномерно распределенной нагрузки соответственно на втором и третьем участках балки; D2, D3 – расстояние от начала координат до конца действия равномерно распределенной нагрузки соответственно на втором и третьем участках балки; L – полная длина балки; L1, L2 – расстояние от начала координат до границы соответственно первого и второго участков. Все размеры принимаются в метрах.
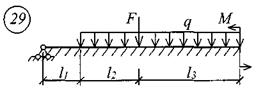
Пример записи исходных данных Для балки (рис. 10) требуется записать исходные данные для расчета на ЭВМ при следующих условиях: F = 400 кН; М = 200 кН×м;
Рис. 10. Расчетная схема
Определение расчетных параметров:
Определение начальных параметров в соответствии с табл. 15. y0 = 0; j0 = 0; M0 ¹ 0; Q0 ¹ 0; yl ¹ 0; jl ¹ 0; Ml = 0; Ql = F = 400 кН. Для определения неизвестных начальных параметров M0 и Q0 записываем уравнения: Ml = 0 и Ql = F. Определение начальных параметров выполняется на ЭВМ. Для каждого участка балки составляются уравнения y, j, М и Q. Запись исходных данных для ЭВМ выглядит следующим образом:
1) Макеев С.А. 22МТ 2) 0,572 1,44 -200 400 100 3 4 3 4 3) 0 0 2,122493 3,711 0 -424,498 0 162,178 0 -1484,258 0 0 0 1,214 2,12249 0 -242,812 0 -371,064 0 -848,996 0 0 0 1 1,748 0 -200 0 -305,638 0 -699,301 0 0 0 -2,289 1 0 457,6 0 -174,825 0 -400 0 4) 3 7 3 0 0 5 7 3 5
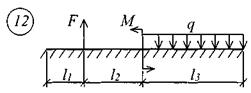
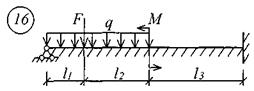
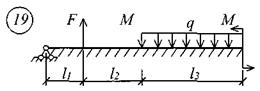
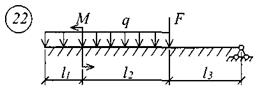
Для решения задачи исходные данные приведены в табл. 18, расчетные схемы балок показаны на рис. 11.
Рис. 11 (начало)
Рис. 11 (окончание)
Таблица 18 Исходные данные к заданию № 11
Библиографический список 1. Александров А.В. Сопротивление материалов: Учеб. для вузов / А.В. Александров, В.Д. Потапов, Б.П. Державин.– М.: Высшая школа, 1995. – 560 с. 2. Сопротивление материалов с основами теории упругости и пластичности: Учеб.для вузов / Под ред. Г.С. Варданяна. – М.: Изд-во АСВ, 1995. – 568 с. 3. Дарков А.В., Шапошников Н.Н. Строительная механика: Учеб. для вузов. – СПб.: Издательство "Лань", 2004. – 656 с. 4. Винокуров Е.Ф. Справочник по сопротивлению материалов / Е.Ф. Винокуров, М.К. Балыкин М.К., И.А. Голубев. – Минск: Наука и техника, 1988. – 464 с. 5. Расчет бруса на внецентренное сжатие: Методические указания к расчетно-проектировочной работе по сопротивлению материалов для студентов строительных специальностей / Сост.: В.Н. Завьялов, Ж.Б. Ищенко, А.Е. Ищенко. – Омск: Изд-во СибАДИ, 1999. – 16 с. 6. Расчетные и курсовые работы по сопротивлению материалов: Учеб. пособие для вузов / Сост.: Ф.З. Алмаметов, С.И. Арсеньев, С.А. Енгалычев. – М.: Высшая школа, 1992. – 320 с. 7. Александров А.В. Основы теории упругости и пластичности: Учеб. для строит. спец. вузов / А.В. Александров, В.Д. Потапов.– М.: Высшая школа, 1990. – 400 с. 8. Построение эпюр внутренних усилий при растяжении, сжатии, кручении и изгибе: Методические указания по сопротивлению материалов для студентов строительных специальностей / Сост.: М.Г. Назаренко. – Омск: Изд-во СибАДИ, 1999. – 15 с. 9. Геометрические характеристики плоских сечений: Методические указания по сопротивлению материалов для студентов строительных специальностей / Сост.: М.Г. Назаренко. – Омск: Изд-во СибАДИ, 1999. – 15 с. 10. Расчет на изгиб балки прокатного профиля: Методические указания для студентов второго курса / Сост.: С.А. Матвеев, Н.Г. Челпанова. – Омск: Изд-во СибАДИ, 1984. – 42 с. 11. Расчет тонкостенных стержней открытого профиля: Методические указания для студентов второго курса / Сост.: М.Г. Назаренко, Т.А. Тверитина. – Омск: Изд-во СибАДИ, 1980. – 37 с. 12. Завьялов В.Н., Мартынов Е.А., Романовский В.М. Основы строительной механики пластин: Учебное пособие. – Омск: Изд-во СибАДИ, 2006. – 115 с.
Содержание Введение …………………………………………………………………….. 3 Задание № 1. Расчет стержня на прочность и жесткость при осевом действии нагрузок ………..…………………………………. 3 Задание № 2. Расчет стержня на прочность и жесткость при кручении… 5 Задание № 3. Определение геометрических характеристик плоских сечений…...…………………………………………………… 7 Задание № 4. Построение эпюр внутренних усилий при поперечном изгибе…...……………………………………………………. 10 Задание № 5. Расчеты на прочность и жесткость при поперечном изгибе ………………………………………………………... 14 Задание № 6. Расчет жесткого бруса на внецентренное сжатие …...…… 17 Задание № 7. Расчет балки на динамическое действие нагрузки……….. 19 Задание № 8. Расчет сжатого гибкого стержня на устойчивость ………. 21 Задание № 9. Определение секториальных характеристик тонкостенного стержня ……………………..…………….… 22 Задание № 10.Расчет пластины методом Ритца …………………………. 24 Задание № 11.Расчет балки на сплошном упругом основании …..…….. 27 Библиографический список …………………………..……………………. 35
Учебное издание
|




 кН×м2;
кН×м2; 1/м.
1/м.