ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задание № 3. Определение геометрических
Характеристик плоских сечений Задано сечение, составленное из двух элементов прокатного профиля и листа. Требуется: 1) определить положение центра тяжести сечения; 2) вычислить осевые и центробежный моменты инерции сечения относительно центральных осей; 3) определить положение главных центральных осей инерции сечения; 4) вычислить величину главных центральных моментов инерции сечения; 5) вычертить в масштабе 1:1 или 1:2 сечение, показать все необходимые оси с указанием расстояний между ними и всеми размерами элементов, входящими в состав сечения; 6) построить эллипс инерции. Исходные данные для решения задачи следует принять по табл. 3, а расчетную схему сечения - по рис. 3.
Таблица 3 Исходные данные к заданию № 3
Для выполнения этой задачи предварительно следует изучить теоретический материал, изложенный в [1], [2], сведения о геометрических характеристиках прокатных профилей (сортаменты) приводятся в этих учебниках и в справочниках [6], [8], [9].
Рис. 3 (начало)
Рис. 3 (окончание)
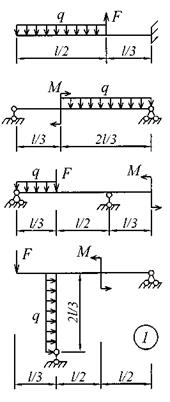
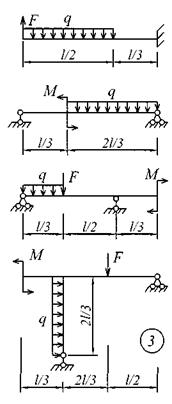
Задание № 4. Построение эпюр внутренних усилий При поперечном изгибе Для четырех заданных расчетных схем стержней требуется: 1) определить опорные реакции; 2) разбить стержень на характерные участки и, пользуясь уравнениями статики, составить аналитические выражения для определения внутренних усилий в произвольном сечении для каждого участка; 3) определить сечения, в которых изгибающий момент имеет экстремальные значения; 4) для каждой схемы построить эпюры внутренних усилий в выбранном масштабе; 5) проверить правильность построения эпюр по дифференциальным зависимостям междуМ, Q и q. Исходные данные для решения этой задачи принять по табл. 4, а расчетные схемы – по рис. 4. Для решения этой задачи необходимо изучить материал, изложенный в [1] – [3], [8], и проанализировать приведенные в этих разделах примеры построения эпюр внутренних усилий. Необходимо запомнить, что инженеры-строители эпюры изгибающих моментов всегда строят только на растянутом волокне!
Таблица 4 Исходные данные к заданию № 4
Рис. 4 (начало)
Рис. 4 (продолжение)
Рис. 4 (окончание)
ЗадаНИЕ № 5. Расчеты на прочность и жесткость При поперечном изгибе Для заданной расчетной схемы балки требуется: 1) определить величину и направление опорных реакций; 2) балку разбить на характерные участки, записать аналитические выражения для внутренних усилий на каждом участке, определить усилия в характерных точках каждого участка, построить эпюры внутренних усилий в выбранном масштабе; 3) по экстремальному значению изгибающего момента из условия прочности по нормальным напряжениям назначить размеры поперечного сечения; 4) используя универсальные уравнения метода начальных параметров, определить величины вертикальных перемещений и углов поворота в характерных сечениях балки и построить эпюру прогибов и эпюру углов поворота; 5) по дифференциальным зависимостям проконтролировать правильность построенных эпюр; 6) составить условие жесткости и назначить размеры поперечного сечения из условия жесткости; 7) сравнить размеры поперечного сечения, назначенные из условия прочности и из условия жесткости; установить окончательные размеры поперечного сечения из обоих условий. Для всех вариантов задания принять: поперечное сечение балки - двутавровый профиль; расчетные сопротивления стали при изгибе Остальные исходные данные для решения этой задачи (размеры пролета и значения приложенных к балке нагрузок для всех вариантов задания) приведены в табл. 5; расчетные схемы балок показаны на рис. 5. Таблица 5 |