ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Исходные данные к заданию № 5
Для выполнения расчетов на прочность и жесткость при поперечномизгибе необходимо изучить материал, который изложен в учебной литературе [1] – [3], [10].
Рис. 5 ЗадаНИЕ № 6. Расчет жесткого бруса на Внецентренное сжатие Для заданного поперечного сечения жесткого бруса с известными координатами точки, в которой приложена сжимающая сила F, требуется: 1) определить положение центра тяжести поперечного сечения; 2) определить положение нейтральной линии и показать ее положение в сечении бруса, вычерченном в выбранном масштабе; 3) из условий прочности на сжатие и растяжение найти предельную величину сжимающей силы; 4) при найденной силе определить нормальные напряжения в характерных точках контура сечения и построить эпюру напряжений в изометрической проекции; 5) построить ядро сечения. Исходные данные для решения этой задачи приведены в табл. 6, а расчетные схемы поперечных сечений бруса показаны на рис. 6. Напряженное состояние брусьев при внецентренном приложении нагрузки анализируется в [1] – [3]; теоретические предпосылки и пример расчета изложены в [5].
Таблица 6 Исходные данные к заданию № 6
Рис. 6 ЗадаНИЕ № 7. Расчет балки на динамическое Действие нагрузки Для заданной расчетной схемы балки, на которую c высоты h падает груз Q, требуется: 1) построить эпюру изгибающих моментов МF от статического действия грузаQ; 2) из условия прочности по нормальным напряжениям назначить размеры поперечного сечения (№ прокатного профиля); 3) методом начальных параметров определить статический прогиб балки в сечении падения груза; 4) определить динамический коэффициент kд (при определении динамического коэффициента массу балки не учитывать); 5) определить величину максимального изгибающего момента с учетом динамического коэффициента и уточнить ранее назначенные размеры сечения балки. Для всех вариантов этой задачи принять модуль упругости материала балки Е = 2×10 5 МПа, остальные исходные данные для решения приведены в табл. 7; расчетные схемы балок показаны на рис. 7.
Таблица 7 Исходные данные к заданию № 7
Рис. 7
ЗАДАНИЕ № 8. Расчет сжатого гибкого Стержня на устойчивость Для заданной расчетной схемы сжатого однопролетного стержня требуется: 1) из условия устойчивости назначить размеры поперечного сечения равноустойчивой (lz = ly) двухветвевой стойки (ветви объединены соединительными планками), применяя метод последовательных итераций; 2) установить возможность применения формул Эйлера или Ясинского для определения критической силы; 3) определить величину критической силы по формуле Эйлера или Ясинского; 4) найти коэффициент запаса устойчивости. Для всех вариантов задачи принять: материал стойки – сталь с расчетным сопротивлением R = 240 МПа, модулем упругости Таблица 8 |













































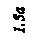










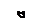
















 15
15