 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Типы сечений двухветвевых стоек
Таблица 9 Исходные данные к заданию № 8
Таблица 10 Виды закрепления стержней
Задание № 9. Определение секториальных Характеристик тонкостенного стержня Для заданного типа поперечного сечения тонкостенного стержня требуется: 1) определить положения центра тяжести сечения; 2) построить эпюры линейных координат z и y; 3) по построенным эпюрам вычислить величину осевых моментов инерции сечения Izс и I yс ; 4) построить эпюру секториальных координат w; 5) перемножением эпюр z и y на эпюру wрассчитать секториально-линейные статические моменты сечения Swz и Swyи определить координаты центра изгиба; 6) построить эпюру главных секториальных координат wо; 7) используя эпюру wо, вычислить главный секториальный момент инерции сечения Iwo; 8) вычислить момент инерции сечения при чистом кручении It . Типы поперечного сечения балки приведены на рис. 8. Исходные данные о размерах сечения следует принять по табл. 11. Перед решением этой задачи необходимо изучить материал, изложенный в [1], [2], [11].
Рис. 8
Таблица 11 Исходные данные к заданию № 9
Задание № 10. Расчет пластины методом Ритца Для прямоугольной пластины, загруженной равномерно распределенной нагрузкой интенсивностью q и сосредоточенной силой величиной F, расположенной в точке K с координатами xF, yF при заданном выражении функции прогибов требуется: 1) установить условия опирания пластины; 2) методом Ритца определить коэффициент C; 3) построить эпюры прогибов для указанных сечений пластин; 4) построить эпюры изгибающих моментов, поперечных сил, крутящих моментов; 5) построить эпюры нормальных и касательных напряжений для указанных сечений. Расчетная схема плиты приведена на рис. 9.
Рис. 9
Из табл. 12 требуется выбрать функцию прогибов, удовлетворяющую граничным условиям на гранях пластины, т.е.
w(x,y) = C ×f i (x)×j j (y),
где i – номер функции в направлении оси х; j – номер функции в направлении оси y.
Цилиндрическая жесткость Эпюры внутренних усилий построить по формулам:
Эпюры строить, исходя из того, что в заданном сечении пластины ее длину и ширину разделить на четыре части. Эпюры напряжений в заданной точке пластины по ее толщине построить согласно формулам:
где z – расстояние по толщине пластины от ее нейтральной плоскости до точки, в которой определяется напряжение. Исходные данные для расчета следует принять по табл. 13.
Таблица 12 Функции прогибов
Таблица 13 Исходные данные к заданию № 10
Задание № 11. Расчет балки на сплошном Упругом основании Для балки, лежащей на сплошном упругом основании требуется определить внутренние усилия и перемещения, используя соответствующие уравнения метода начальных параметров. Работа выполняется в два этапа. На первом этапе необходимо записать уравнения деформаций и внутренних усилий для каждого участка балки. Напряженно-деформированное состояние балки, лежащей на сплошном упругом основании, зависит от жесткостных характеристик балки и упругого основания. Этими характеристиками являются: EJz – изгибная жесткость балки;
где Е – модуль упругости материала балки, кН/м2; Jz – момент инерции поперечного сечения балки, м4; K0 – коэффициент податливости упругого основания, зависящий от свойств грунта, кН/м3; b – ширина поперечного сечения балки, м. При расчете методом начальных параметров начало координат выбирается в крайней левой точке балки. Поскольку реакция упругого основания изменяется непрерывно по длине балки, то для построения криволинейных эпюр деформаций и внутренних усилий необходимо определить их значения для нескольких точек по длине. Начальные параметры зависят от граничных условий. В табл. 14 представлены уравнения в зависимости от действующих внешних нагрузок. В этих уравнениях y0, j0, M0, Q0 – начальные параметры, из которых два всегда равны нулю (табл. 15). Неизвестные начальные параметры определяются из условий закрепления правого края балки. В уравнения y, j, M, Q (табл. 14) входят функции Y1(x), Y2(x), Y3(x), Y4(x), названные функциями Крылова-Коши, значения которых определяются в зависимости от аргумента bx, где x – координаты точек балки в принятой системе координат:
Y1(x) = chbx × cosbx; Y2(x) = 0,5(chbx × sinbx + shbx × cosbx); Y3(x) = 0,5shbx × sinbx; Y4(x) = 0,25(chbx × sinbx – shbx × cosbx).
В зависимости от характера действующих нагрузок и от условий закреплений левого конца балки для каждого участка необходимо записать уравнение по форме, представленной в табл. 14. Поскольку при составлении уравнений для различных сечений каждый раз рассматривается часть балки слева от сечения, то в уравнение для каждого последующего сечения входят все слагаемые уравнения в предыдущих сечениях. Поэтому запись уравнений для любого сечения может быть представлена в виде табл. 16.
|
Профиль 
Конструкция опорных закреплений сжатой стойки
.
.
;
;
;
;
.
;
;
,
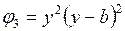
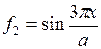
– коэффициент жесткости,