 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Уравнения в полных дифференциалах и их решение
Цель:Изучение уравнений в полных дифференциалах и их решения. Задачи: 1. Ввести понятия уравнения в полных дифференциалах. 2. Рассмотреть необходимое и достаточное условие уравнения в полных дифференциалах. 3. Рассмотреть способ решения уравнения в полных дифференциалах. Желаемый результат: Студенты должны знать уравнения в полных дифференциалах и способ их решения. Учебные вопросы: 1. Уравнения в полных дифференциалах. 2. Необходимое и достаточное условие уравнения в полных дифференциалах. 3. Решение уравнения в полных дифференциалах.
Определение и решение дифференциальных уравнений в полных дифференциалах Если левая часть уравнения:
представляет собой полный дифференциал некоторой функции
то уравнение (1) называется уравнением в полных дифференциалах.
В этом случае его можно записать так:
Откуда интегрированием получаем общий интеграл
Например, легко проверить, что левая часть уравнения
есть полный дифференциал функции Поэтому уравнение можно записать в виде: Естественно, возникает вопрос: при каких условиях уравнение (1) представляет собой уравнение в полных дифференциалах Ответом на этот вопрос служит следующая теорема: Теорема. Для того чтобы дифференциальное выражение
где функции
Доказательство: Докажем сначала необходимость этого условия. Для этого предположим, что существует такая функция Полным дифференциалом функции
Так как оно равно выражению (2), то мы имеем тождество
справедливое для любых Сравнивая множители при
Продифференцируем обе части первого равенства по
Из равенства смешанных производных и необходимость этого условия доказана. Докажем теперь достаточность этого условия. Для этого предположим, что условие (3) имеет место. Докажем, что выражение (2) представляет собой полный дифференциал некоторой функции
Тем самым задача сводится к отысканию функции Возьмем первое из уравнений (4). Его решение можно записать в виде:
где
Так как то По условию
Последний интеграл равен:
Поэтому
где Подставляя найденное выражение
Итак, доказано не только существование функции Пример: Проверим, что дифференциальное выражение
представляет собой полный дифференциал Решение. В данном случае
Следовательно, условие Найдем функцию
Первое из этих уравнений дает:
Так как
Находим из этого выражения
Следовательно,
Если бы надо было проинтегрировать дифференциальное уравнение:
то, переписав его в виде
мы получили бы общий интеграл
Пример: Пусть дано дифференциальное уравнение:
Выберем из семейства интегральных кривых этого уравнения ту, которая проходит через начало координат. Здесь Так как то условие Остается найти функцию
Из первого уравнения находим
Дифференцируем полученное выражение по
Приравнивая выражения
Интегрируем обе части, получаем
Итак, уравнение семейства интегральных кривых имеет вид:
Уравнение искомой интегральной кривой найдем, зная, что из начального условия Окончательно имеем:
Вопросы для самопроверки: 1. Какие уравнения называются уравнениями в полных дифференциалах? 2. Сформулировать необходимое и достаточное условие уравнения в полных дифференциалах. 3. Как найти решение уравнения в полных дифференциалах?
|



 (1)
(1) , т.е.
, т.е. ,
,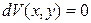 .
. .
.
 .
. . Откуда находим общий интеграл:
. Откуда находим общий интеграл:  .
. и как найти функцию
и как найти функцию  ?
? , (2)
, (2) и
и 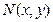 определены и непрерывны в области
определены и непрерывны в области  плоскости
плоскости  и имеют в ней непрерывные частные производные
и имеют в ней непрерывные частные производные  и
и  , представляло собой полный дифференциал некоторой функции
, представляло собой полный дифференциал некоторой функции  . (3)
. (3) и докажем, что имеет место равенство (3).
и докажем, что имеет место равенство (3). .
. ,
, и
и  .
.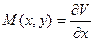 ;
; 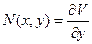 .
. , а второго по
, а второго по  :
: ;
;  .
. заключаем, что
заключаем, что 
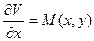 ;
;  . (4)
. (4) , (5)
, (5) - абсцисса какой-либо точки
- абсцисса какой-либо точки  области
области  - произвольная функция от
- произвольная функция от  , поскольку интегрирование производится по
, поскольку интегрирование производится по  в предположении, что
в предположении, что 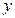 сохраняет неизменное значение. Определим
сохраняет неизменное значение. Определим  так, чтобы удовлетворялось и второе из уравнений (4). Продифференцируем обе части равенства (5) по
так, чтобы удовлетворялось и второе из уравнений (4). Продифференцируем обе части равенства (5) по  .
. , а согласно теореме о дифференцировании определенного интеграла по параметру
, а согласно теореме о дифференцировании определенного интеграла по параметру  ,
, .
. .
. .
. , откуда
, откуда ,
, - ордината точки
- ордината точки  области
области  . (6)
. (6) , но даже выведена формула для нахождения этой функции.
, но даже выведена формула для нахождения этой функции.
 и найдем функцию
и найдем функцию 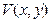 .
. ;
;  ;
; ;
; 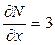 .
. ;
;  .
. .
. (получено при дифференцировании функции
(получено при дифференцировании функции  (из условия примера) то имеем:
(из условия примера) то имеем: .
. :
: или
или 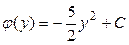 .
. .
. ,
, ,
, .
.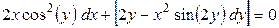 .
. ;
;  .
. ,
,  ,
, ;
;  .
. .
. .
. , будем иметь
, будем иметь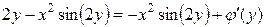 или
или 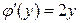 .
. .
. .
. при
при 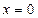 следует, что
следует, что  .
. .
.