 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Дифференциальные уравнения первого порядка.
Дифференциальные уравнения. Основные определения. Цель:Изучение основных понятий дифференциальных уравнений. Задачи: 1. Ввести понятие обыкновенного дифференциального уравнения и дифференциального уравнения в частных производных. 2. Дать понятие порядка дифференциального уравнения. 3. Дать определение дифференциального уравнения п-го порядка. 4. Рассмотреть общее и частное решения дифференциального уравнения п-го порядка. 5. Рассмотреть задачу Коши дифференциального уравнения п-го порядка. 6. Дать определение дифференциального уравнения первогопорядка. 7. Рассмотреть общее и частное решения дифференциального уравнения первогопорядка. 8. Рассмотреть задачу Коши дифференциального уравнения первогопорядка. Желаемый результат: Студенты должны знать основные понятия дифференциальных уравнений. Учебные вопросы: 1. Обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных. 2. Порядок дифференциального уравнения. 3. Дифференциальное уравнение п-го порядка. 4. Общее и частное решения дифференциального уравнения п-го порядка. 5. Задача Коши дифференциального уравнения п-го порядка. 6. Дифференциальное уравнение первогопорядка. 7. Общее и частное решения дифференциального уравнения первогопорядка. 8. Задача Коши дифференциального уравнения первогопорядка.
Дифференциальные уравнения. Основные определения Пусть функция Рассмотрим пример. С некоторой высоты брошено тело, масса которого Решение: По второму закону Ньютона:
где
Мы получили соотношение, связывающее неизвестную функцию Решить дифференциальное уравнение - это значит найти такую функцию Легко проверить, что всякая функция вида:
удовлетворяет уравнению (1), каково бы ни было постоянное число C. Какая же из этих функций даст искомую зависимость Но тогда искомая функция
Откуда
Таким образом, постоянная
Заметим, что если t =0 (т.е. сопротивление воздуха отсутствует, или оно столь мало, что им можно пренебречь), то мы получаем известный из физики результат: Эта функция удовлетворяет дифференциальному уравнению (I) и начальному условию: Во всех случаях при выборе дифференциального уравнения в физике или технике берется за основу некоторый общий физический закон или какой-либо ещё, имеющий дифференциальный характер (дифференциальный закон), т.е. связывающий бесконечно малые изменения рассматриваемых величин. После интегрирования уравнения получается интегральный закон, связывающий конечные значения этих величин. Определение I. Дифференциальным уравнением называется уравнение, связывающее независимую переменную
или
Если искомая функция Дифференциальным уравнением в частных производных называется отношение между неизвестной функцией z зависящей от двух или нескольких переменных х.у,.., этими переменными х,у,... и частными производными от z Определение 2. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например, уравнение: Уравнение: Определение 3. Решением или интегралом дифференциального уравнения называется всякая функция Уже на простейших примерах можно убедиться в том, что дифференциальное уравнение имеет бесчисленное множество решений. Например, из уравнения:
решение определяется с помощью интегрирования:
Это есть общее решение уравнения (5), оно включает произвольную постоянную С и является записью всего многообразия решений. Придавая произвольной постоянной конкретные численные значения, мы получим частные решения:
В общем случае для уравнения n-го порядка
решение находится в результате n последовательных интегрирований, так что общее решение уравнения n-го порядка содержит n произвольных постоянных, т.е. имеет вид:
Особенно часто общее решение получается в неявной форме:
Частные решения получаются, если придать каждой произвольной постоянной С График каждого частного решения называется интегральной линией рассматриваемого дифференциального уравнения. Уравнение этой линии - это уравнение (7) и (8) с конкретными С. Чтобы из общего решения выделить одно частное, требуется, помимо дифференциального уравнения, поставить некоторые дополнительные условия. Чаще вето ставятся начальные условия, которые при исследовании процесса, развивающегося во времени, являются математической записью начального состояния процесса. Задача о нахождении частного решения дифференциального уравнения при заданном начальном условии называется задачей Коши. Дифференциальные уравнения первого порядка Дифференциальное уравнение первого порядка имеет вид:
Если это уравнение можно разрешить относительно В этом случае говорят, что дифференциальное уравнение разрешено относительно производной. Для такого уравнения справедлива следующая теорема, которая называется теоремой о существовании и единственности решения дифференциального уравнения. Теорема. Если в уравнении Без доказательства. Геометрический смысл теоремы заключается в том, что существует и притом единственная функция Условие, что при
Определение I. Общим решением дифференциального уравнения первого порядка называется функция: которая зависит от одного произвольного постоянного а) Она удовлетворяет дифференциальному уравнению при любом конкретном значении постоянного б) Каково бы ни было начальное условие В процессе нахождения общего решения дифференциального уравнения нередко приходит к соотношению вида:
не разрешенному относительно у. Разрешив это соотношение относительно у, получаем общее решение. Однако выразить у из соответствующего соотношения (2*) в элементарных функциях не всегда оказывается возможным, в таких случаях общее решение оставляется в неявном виде. Равенство вида Определение: Частным решением называется любая функция y= Соотношение
Вопросы для самопроверки: 1. Какие уравнения называются обыкновенными дифференциальными уравнениями, дифференциальными уравнениями в частных производных? 2. Как найти порядок дифференциального уравнения? 3. Какие уравнения называются дифференциальными уравнениями п-го порядка? 4. Дать понятие общего и частного решений дифференциального уравнения п-го порядка. 5. Сформулировать задачу Коши дифференциального уравнения п-го порядка. 6. Какое уравнение называется дифференциальным уравнением первогопорядка? 7. Какое решение называется общим и частным решением дифференциального уравнения первогопорядка. 8. Сформулировать задачу Коши дифференциального уравнения первогопорядка.
ЛЕКЦИЯ № 18 |



 отражает количественную сторону некоторого явления. Очень часто, рассматривая это явление нельзя непосредственно установить характер зависимости
отражает количественную сторону некоторого явления. Очень часто, рассматривая это явление нельзя непосредственно установить характер зависимости 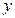 от
от  , а можно установить зависимость между величинами
, а можно установить зависимость между величинами  ,
,  ,…,
,…, 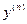 , т.е. написать дифференциальное уравнение. Требуется из полученной зависимости найти
, т.е. написать дифференциальное уравнение. Требуется из полученной зависимости найти  . Требуется установить, по какому закону будет изменяться скорость
. Требуется установить, по какому закону будет изменяться скорость 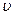 падения этого тела, если на него кроме силы тяжести, действует тормозящая сила сопротивления воздуха, пропорциональная скорости с коэффициентом пропорциональности
падения этого тела, если на него кроме силы тяжести, действует тормозящая сила сопротивления воздуха, пропорциональная скорости с коэффициентом пропорциональности  (т.е. требуется найти
(т.е. требуется найти  ).
).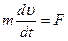 ,
, - есть ускорение движущегося тела (производная от скорости по времени), а F- сила, действующая на тело, в направлении движения. Эта сила складывается из двух: силы тяжести mg и силы сопротивления воздуха -
- есть ускорение движущегося тела (производная от скорости по времени), а F- сила, действующая на тело, в направлении движения. Эта сила складывается из двух: силы тяжести mg и силы сопротивления воздуха -  (мы берем её с минусом, ибо она направлена в сторону, противоположную направлению скорости). Итак:
(мы берем её с минусом, ибо она направлена в сторону, противоположную направлению скорости). Итак: (1)
(1) (2)
(2) , которая известна.
, которая известна. . Подставляя t=0,
. Подставляя t=0, 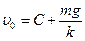 .
. .
. найдена. Следовательно, искомая зависимость такова:
найдена. Следовательно, искомая зависимость такова: . (3)
. (3) (4)
(4) и её производные
и её производные  , …,
, …, 
 .
. и т.д.
и т.д. - уравнение 1-го порядка.
- уравнение 1-го порядка. - уравнение 2-го порядка и т.д.
- уравнение 2-го порядка и т.д. (5)
(5) .
. ;
;  и т.д.
и т.д.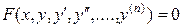 (6)
(6) . (7)
. (7)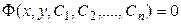 (8)
(8) ,С
,С  ,.., С
,.., С  конкретное численное значение.
конкретное численное значение. (1)
(1) , то его можно записать в виде:
, то его можно записать в виде:  (1*)
(1*) функция
функция  и её частная производная
и её частная производная  по
по  непрерывны в некоторой области
непрерывны в некоторой области  на плоскости
на плоскости  , содержащей некоторую точку
, содержащей некоторую точку  , то существует единственное решение этого уравнения
, то существует единственное решение этого уравнения 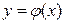 , удовлетворяющее условию: при
, удовлетворяющее условию: при  ,
,  .
. , график которой проходит через точку
, график которой проходит через точку 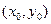 .
. функция
функция  называется начальным условием. Она часто записывается в виде:
называется начальным условием. Она часто записывается в виде: .
. , (2)
, (2) при
при  можно найти такое значение
можно найти такое значение  , что функция
, что функция  удовлетворяет данному начальному условию. При этом предполагается, что значения
удовлетворяет данному начальному условию. При этом предполагается, что значения  и
и  , (2*)
, (2*) , которая получается из общего решения y=
, которая получается из общего решения y=  , если в последнем произвольному постоянному С придать значение С=
, если в последнем произвольному постоянному С придать значение С=  .
. (x,y,
(x,y,  =0 называется в этом случае частным интегралом уравнения.
=0 называется в этом случае частным интегралом уравнения.