 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Уравнение Бернулли и его решение
Цель:Изучение дифференциальных уравнений первого порядка и способов их решений. Задачи: 1. Рассмотреть решение линейного дифференциального уравнения методом вариации произвольной постоянной. 2. Дать определение уравнения Бернулли. 3. Рассмотреть решение уравнения Бернулли. Желаемый результат: Студенты должны знать метод вариации произвольной постоянной, а также уравнение Бернулли и его решение. Учебные вопросы: 1. Решение линейного дифференциального уравнения методом вариации произвольной постоянной. 2. Уравнение Бернулли. 3. Решение уравнения Бернулли. Решение линейных уравнений первого порядка методом вариации произвольной постоянной Пусть дано дифференциальное уравнение вида:
Решим сначала соответствующее ему однородное уравнение:
которое является уравнением с разделяющимися переменными. Его общее решение
Совершенно очевидно, что найденная функция Для нахождения функции
уравнение (1) переходит в уравнение
(два средних члена взаимно уничтожились). Мы опять получили уравнение с разделяющимися переменными и неизвестной функцией
Подставляя найденное выражение
Название способа происходит от того, что мы варьируем (изменяем) произвольную постоянную Этот способ, как и способ Бернулли, позволяет свести линейное уравнение (1) к двум уравнениям с разделяющимися переменными. Пример: Найти общее решение линейного уравнения
методом вариации произвольной постоянной. Сначала находим общее решение линейного однородного уравнения
Разделение переменных приводит это уравнение к виду
откуда Будем варьировать
Выражения
или после упрощений:
откуда Подставляя выражение
Уравнение Бернулли и его решение
Общий вид уравнения Бернулли
где При
и, следовательно, может быть проинтегрировано разделением переменных. В дальнейшем будем предполагать, что Уравнение Бернулли можно подстановкой привести к линейному виду. Для этого разделим обе части уравнения на
Положим
тогда и уравнение Бернулли принимает вид:
Это линейное уравнение первого порядка с неизвестной функцией Возвращаясь к первоначальному переменному Пример: Найти общий интеграл уравнения Бернулли
Решение. Разделив обе части уравнения на
Положим Уравнение принимает вид:
Это линейное уравнение и будем его интегрировать методом вариации произвольной постоянной. Общее решение однородного уравнения
Полагаем, что
и подставим в линейное неоднородное уравнение. Получаем:
или
откуда
и, следовательно, общее решение неоднородного уравнения
Вернемся к переменной у, получим
или окончательно
Практически более удобным является решение уравнения Бернулли с помощью подстановки Пример. Решить уравнение Бернулли
Решение: Положим
Функцию
Находим функцию Интегрируя это выражение, имеем:
Тогда окончательно для
Так что общее решение имеет вид:
Вопросы для самопроверки: 1. Рассказать о решении линейного дифференциального уравнения методом вариации произвольной постоянной. 2. Какое уравнение называется уравнением Бернулли? 3. Как решить уравнение Бернулли?
ЛЕКЦИЯ № 21 |



 . (1)
. (1) , (2)
, (2) . (3)
. (3) не может быть решением неоднородного уравнения, т.к. при подстановке в уравнение (1) она обратит левую часть в нуль, в то время как правая часть
не может быть решением неоднородного уравнения, т.к. при подстановке в уравнение (1) она обратит левую часть в нуль, в то время как правая часть  не равна нулю. Если рассматривать
не равна нулю. Если рассматривать  не как константу, а как функцию от
не как константу, а как функцию от  , т.е.
, т.е.  , то можно подобрать функцию
, то можно подобрать функцию  так, чтобы функция (3) стала решением неоднородного уравнения (1).
так, чтобы функция (3) стала решением неоднородного уравнения (1). вычислим производную функции
вычислим производную функции  ,
, , (4)
, (4) . Его общее решение:
. Его общее решение: .
. . (5)
. (5) .
.
 .
. ,
, и
и  .
. и
и .
. и
и  подставим в исходное уравнение, получим:
подставим в исходное уравнение, получим:
 ;
;  ;
; .
. .
. , (6)
, (6) .
. уравнение Бернулли переходит в линейное уравнение, при
уравнение Бернулли переходит в линейное уравнение, при  оно является уравнением с разделяющимися переменными, так как может быть преобразовано, к виду:
оно является уравнением с разделяющимися переменными, так как может быть преобразовано, к виду:
 .
.
 .
. ,
,
 ,
,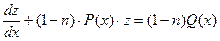 .
. , его можно проинтегрировать способом подстановки или способом вариации произвольного постоянного и найти
, его можно проинтегрировать способом подстановки или способом вариации произвольного постоянного и найти  как функцию от
как функцию от  , получим общий интеграл уравнения Бернулли.
, получим общий интеграл уравнения Бернулли. .
. получим:
получим: .
. ;
;  .
. или
или  .
. ,
,  ,
,  .
.

 ,
,  ,
,
 .
.
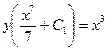 .
.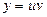 (не сводя его к линейному).
(не сводя его к линейному). .
. , тогда
, тогда  , подставляя эти значения в уравнение, получим
, подставляя эти значения в уравнение, получим ,
,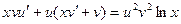 .
. найдем, как частное решение уравнения:
найдем, как частное решение уравнения: ;
; 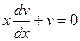 ;
;  ;
;  ;
;  .
. :
:  ;
;  ;
;  ;
;  .
. ;
; ;
;  ;
;  ;
;  ;
; .
.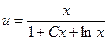 .
. .
.