 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Электрическое поле и его характеристики
Электрическим полем называется особая форма существования материи, способная передавать электрическое взаимодействие. Свойства поля:
1. Поле не имеет границ, оно бесконечно. 2. Электрическое взаимодействие передается с конечной скоростью (в вакууме со скоростью света c). 3. Поле обладает энергией. 4. Поле обладает массой. Напряженность поля Основной силовой характеристикой поля в вакууме является напряженность:
Напряженность поля, создаваемого зарядом Q в точке A зависит от заряда Q и от расстояния r:
Напряженность – это физическая величина, численно равная силе, действующей на единичный положительный заряд, помещенный в данную точку поля:
Напряженность поля точечного заряда в скалярной и векторной форме определяется по формулам:
Принцип суперпозиции полей Каждый из зарядов в отдельности создаст в данной точке поле независимо от полей, создаваемых другими зарядами. Суперпозиция означает наложение:
Рис. 2.6.
Силовые линии Для символического изображения напряженности Фарадей предложил использовать силовые линии. Силовые линии – это линии, касательные к которым в каждой точке совпадают с направлением силы, действующей на положительный заряд, помещенный в эту точку. Они начинаются на положительных и заканчиваются на отрицательных зарядах. Если рассмотреть некоторый уединенный точечный заряд, то линии напряженности обязательно закончатся на отрицательном заряде, который, возможно, на чертеже и не уместится. Чем больше величина напряженности электростатического поля, тем выше густота силовых линий. Количество линий напряженности (или силовых линий), пронизывающих единичную площадку, численно равно значению напряженности электростатического поля. Рассмотрим важнейшие случаи пространственного расположения зарядов и форму силовых линий полей этих зарядов. Опыт 2.3. Силовые линии электрического поля[8,9] Оборудование: 1. Султаны на изолирующих штативах 2. Электрофорная машина 3. Провода соединительные
Рис. 2.7. Простейшая демонстрация электрических силовых линий выполняется при помощи султанов, которые устанавливаются на изолирующих штативах и заряжаются хорошо наэлектризованной палочкой или от электрофорной машины. Сначала показыва.т опыт с одним заряженным султаном и обращают внимание на радиальное положение бумажных полосок (рис.2.7., а). Затем заряжают оба султана одноименными (рис. 2.7., б) и разноименными зарядами (рис.2.7., в) и показывают искривление при отталкивании и притяжении.
а б
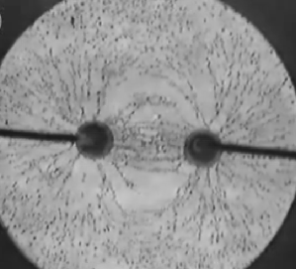
в г Рис. 2.8. На рис.2.8 изображены силовые линии электрических полей в простейших случаях: а, б) уединенный точечный заряд (“+”или “-” ); в) два одноименных точечных заряда; г) два разноименных точечных заряда. Опыт 2.4.Визуализация силовых линий поля. Цель работы: Визуализировать силовые линии поля. Оборудование: 1. Высоковольтный источник питания; 2. Касторовое масло; 3. Мелкие диэлектрические частицы 4. Электроды;
Рис. 2.9. К полюсам высоковольтного источника питания подсоединены электроды, погруженные в касторовое масло, в котором находятся мелкие диэлектрические частицы. 1. Вблизи электрода возникает электростатическое поле, и эти частицы ориентируются вдоль поля, образуя хорошо видимые цепочки, напоминающие силовые линии электрического поля.
Рис.2.10. 2. Если взять два практически точечных электрода и подать на них заряды одинакового знака, то картина силовых линий будет выглядеть следующим образом. Силовые линии словно отталкиваются друг от друга.
Рис.2.10. 3. Если подать разноименные заряды, то картина изменится. Теперь силовые линии идут от тела с зарядом одного знака к телу с зарядом другого знака.
Рис.2.11. 4. Модель плоского конденсатора. При включении напряжения, основная часть электрического поля сосредоточена внутри между пластинами. Оно там является практически однородным. В остальной области пространства поле слабое.
Рис.2.12. 5. Модель цилиндрического конденсатора. Поле существует только между внутренним и внешними цилиндрами, где мы видим цепочки мелких диэлектрических частиц. В остальных областях пространства оно практически отсутствует.
Рис.2.13. Вывод: Силовые линии каждой из представленных моделей различны. Тесты к лекции №2. Тест 2.1.Каков знак произведения для одноименных зарядов?
£
£
£
£ Тест 2.2.Выберите все правильные ответы. К свойствам электрического заряда относятся: £ Наличие дискретной природы £ Взаимодействие между зарядами (одноименные - отталкиваются, разноименные притягиваются) £ Зависимость от системы отсчета £ Наличие особого вида материи £ Потенциальность Тест 2.3. Какой формулой выражается закон Кулона? £
£
£
£ Тест 2.4. Как называется следующий закон: "Сила электростатического взаимодействия двух точечных электрических зарядов в вакууме прямо пропорциональна произведению величин этих зарядов и обратно пропорциональна квадрату расстояния между ними "? £ Закон Кулона £ Закон Ома £ Закон взаимодействия электрических зарядов £ Закон взаимодействия точечных электрических зарядов Тест 2.5 На концах невесомого стержня длиной 1 м находятся два невесомых шарика с зарядами +1 Кл и -1 Кл. На перпендикуляре, проведенном через середину стержня, на расстоянии 0,5 м от основания перпендикуляра расположен точечный заряд 1 Кл. Определить вращающий момент (в кН*м), действующий на стержень. £ 1,1 £ 2,2 £ 1,3 £ 1,4 £ 2,6
Теорема Остроградского – Гаусса и ее применение[11] 3.1. Основные определения. 3.2. Теорема Остроградского – Гаусса для дискретного и непрерывного распределения зарядов. 3.3. Применение теоремы Остроградского – Гаусса для случаев: 3.3.1. Заряженная плоскость. 3.3.2. Две разноименно заряженные плоскости. 3.3.3. Заряженная нить. 3.3.4. Заряженная сфера. 3.3.5. Заряженный шар. 3.4. Аналогия между электростатическим и гравитационным полями. Основные определения 1. Линейная плотность заряда
Рис. 3.1.
Если 2. Поверхностная плотность заряда
Рис. 3.2.
3. Объемная плотность заряда
Рис. 3.3.
4.
где
– поток через замкнутую поверхность. |
Рис. 2.5.
.
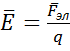
– это физическая величина, численно равная заряду, приходящемуся на единицу длины:
(3.1)
. (3.1.1)
– это физическая величина, численно равная заряду, приходящемуся на единицу площади.
(3.2)
. (3.2.1)
– это физическая величина, численно равная заряду, заключенному в единице объема
. (3.3)
. (3.3.1)
– стационарное поле.
Рис. 3.4.
, (3.4)
, (3.5)
– единичная нормаль к поверхности S.
(3.6)